[笔记] binarySearchTree AVLTree

binary search tree

search tree operations

1.tree()
2.put(key,value)
3.get(key)
4.in()
5.delete()
6.len()

binary search tree node

class TreeNode(object):
    def __init__(self,key,val,left=None,right=None,parent=None):
        self.key = key
        self.val = val
        self.left = left
        self.right = right
        self.parent = parent
        self.balanceFactor = 0

    def hasLeftChild(self):
        return self.left

    def hasRightChild(self):
        return self.right

    def isLeftChild(self):
        return self.parent and self.parent.left is self

    def isRightChild(self):
        return self.parent and self.parent.right is self

    def isRoot(self):
        return not self.parent

    def isLeaf(self):
        return not (self.left or self.right)

    def hasAnyChildren(self):
        return self.left or self.right

    def hasBothChildren(sefl):
        return self.left and self.right

    def replaceNodeData(self,newKey,newVal,lf,ri):
        self.key = newKey
        self.val = newVal
        self.left = lf
        self.right = ri
        if self.hasLeftChild():
            self.left.parent = self
        if self.hasRightChild():
            self.right.parent = self

    def findSuccessor(self):
        succ = None
        if self.hasRightChild():
            succ = self.right.findMin()
        elif self.parent:
            if self.isLeftChild():
                succ = self.parent
            else:
                self.parent.right = None
                succ = self.parent.findSuccessor()
                self.parent.right = self
        return succ

    def findMin(self):
        cur = self
        while cur.hasLeftChild():
            cur = cur.left
        return cur

    def spliceOut(self):
        if self.isLeaf():
            if self.isLeftChild():
                self.parent.left = None
            else:
                self.parent.right = None
        elif self.hasAnyChildren():
            if self.hasLeftChild():
                if self.isLeftChild():
                    self.left.parent = self.parent
                    self.parent.left = self.left
                else:
                    self.parent.right = self.left
                    self.left.parent = self.parent
            else: # ####### 
                if self.isLeftChild():
                    self.parent.left = self.right
                    self.right.parent = self.parent
                else:
                    self.right.parent = self.parent
                    self.parent.right = self.right



class BinarySearchTree(object):

    def __init__(self):
        self.size = 0
        self.root = None

    def length(self):
        return self.size

    def __len__(self):
        return self.size

    def __iter__(self):
        return self.root.__iter__()

    def put(self,key,val):
        if self.root:
            self._put(key,val,self.root)
        else:
            self.root = TreeNode(key,val)
        self.size += 1

    def _put(self,key,val,curNode):
        if key<curNode.key:
            if curNode.hasLeftChild():
                self._put(key,val,curNode.left)
            else:
                curNode.left = TreeNode(key,val,parent=curNode)
        else:
            if curNode.hasRightChild():
                self._put(key,val,curNode.right)
            else:
                curNode.right = TreeNode(key,val,parent=curNode)

    def __setitem__(self,key,val):
        self.put(key,val)

    def get(self,key):
        if self.root:
            res = self._get(key,self.root)
            if res:
                return res.val
            else:
                return None
        else:
            return None

    def _get(self,key,curNode):
        if not curNode:
            return None
        if curNode.key == key:
            return curNode
        if curNode.key > key:
            return self._get(key, curNode.left)
        if curNode.key < key:
            return self._get(key, curNode.right)

    def __getitem__(self,key):
        return self.get(key)

    def __contains__(self,key):
        if self._get(key,self.root):
            return True
        else:
            return False

    def delete(self,key):
        if self.size>1:
            res = self._get(key)
            if not res:
                raise KeyError('Error, key not in tree')
            else:
                self.remove(res)
                self.size -= 1
        elif self.size == 1 and self.root.key == key:
            self.root = None
            self.size = 0
        else:
            raise KeyError('Error, key not in tree')

    def __del__(self,key):
        self.delete(key)

    def remove(curNode):
        if curNode.isLeaf():
            if curNode.parent.left is curNode:
                curNode.parent.left = None
            else:
                curNode.parent.right = None
        elif curNode.hasBothChildren():
            suc = curNode.findSuccessor()
            suc.spliceOut()
            curNode.key = suc.key
            curNode.val = suc.val
        else: # only one child
            if curNode.hasLeftChild():
                if curNode.isLeftChild():
                    curNode.left.parent = curNode.parent
                    curNode.parent.left = curNode.left
                elif curNode.isRightChild():
                    curNode.left.parent = curNode.parent
                    curNode.parent.right = curNode.left
                else: # root self.root = curNode.left
                    curNode.replaceNodeData(curNode.left.key,
                                            curNode.left.val,
                                            curNode.left.left,
                                            curNode.left.right)
            else:
                if curNode.isLeftChild():
                    curNode.right.parent = curNode.parent
                    curNode.parent.left = curNode.right
                elif curNode.isRightChild():
                    curNode.right.parent = curNode.parent
                    curNode.parent.right = curNode.right
                else:
                    curNode.replaceNodeData(curNode.right.key,
                                            curNode.right.val,
                                            curNode.right.left,
                                            curNode.right.right)




mytree = BinarySearchTree()
mytree[3]="red"
mytree[4]="blue"
mytree[6]="yellow"
mytree[2]="at"

print(mytree[6])
print(mytree[2])


yellow
at

AVL tree

class AVLtree(BinarySearchTree):

    def _put(self,key,val,curNode):
        if key<curNode.key:
            if curNode.hasLeftChild():
                self._put(key,val,curNode.left)
            else:
                curNode.left = TreeNode(key,val,parent=curNode)
                self.updateBalance(curNode.left)
        else:
            if curNode.hasRightChild():
                self._put(key,val,curNode.right)
            else:
                curNode.right = TreeNode(key,val,parent=curNode)
                self.updateBalance(curNode.right)

    def updateBalance(self,node):
        if node.balanceFactor>1 or node.balanceFactor<-1:
            self.rebalance(node)
            return
        if node.parent:
            if node.isLeftChild():
                node.parent.balanceFactor += 1
            elif node.isRightChild():
                node.parent.balanceFactor -= 1
            if node.parent.balanceFactor != 0:
                self.updateBalance(node.parent)

    def rotateLeft(self,rotRoot):
        newRoot = rotRoot.right
        newRoot.parent = rotRoot.parent
        rotRoot.right = newRoot.left
        if newRoot.left is not None:
            newRoot.left.parent = rotRoot
        if rotRoot.isRoot():
            self.root = newRoot
        else:
            if rotRoot.isLeftChild():
                rotRoot.parent.left = newRoot
            else:
                rotRoot.parent.right = newRoot
        newRoot.left = rotRoot
        rotRoot.parent = newRoot
        rotRoot.balanceFactor += 1-min(newRoot.balanceFactor,0)
        newRoot.balanceFactor += 1+max(rotRoot.balanceFactor,0)

    def rotateRight(self,rotRoot):
        newRoot = rotRoot.left
        rotRoot.left = newRoot.right
        if newRoot.right is not None:
            newRoot.right.parent = rotRoot
        newRoot.parent = rotRoot.parent
        if rotRoot.isRoot():
            self.root = newRoot
        else:
            if rotRoot.isLeftChild():
                rotRoot.parent.left = newRoot
            else:
                rotRoot.parent.right = newRoot
        newRoot.right = rotRoot
        rotRoot.parent = newRoot
        rotRoot.balanceFactor += -1-min(newRoot.balanceFactor,0)
        newRoot.balanceFactor += -1+max(rotRoot.balanceFactor,0)

    def rebalance(self,node):
        if node.balanceFactor < 0:
            if node.right.balanceFactor > 0:
                self.rotateRight(node.right)
                self.rotateLeft(node)
            else:
                self.rotateLeft(node)
        else:
            if node.left.balanceFactor < 0:
                self.rotateLeft(node.left)
                self.rotateRight(node)
            else:
                self.rotateRight(node)

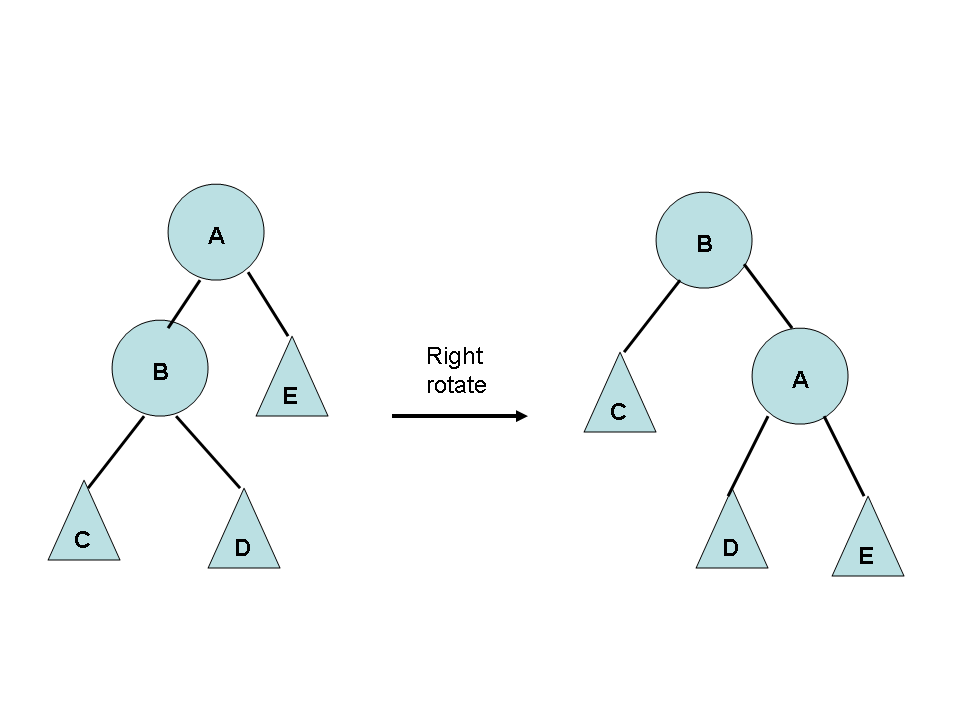
how to compute the new balance factor?
1. 计算B的平衡因子
$oldbalance(B) = h_{c} - h_{d}$
$newbalance(B) = h_{c} - 1 - max(h_{d}-h_{e})$
$newbalance(B) - oldbalance(B) = -1 - max(h_{d},h_{e}) + h_{d}$
$= -1 + max(h_{d}-h_{e},0)$
$= -1 + max(newbalance(A),0)$

2.计算A的平衡因子
$oldbalance(A) = 1 + max(h_{c}, h_{d}) - h_{e}$
$newbalance(A) = h_{d} - h_{e}$
$newbalance(A) - oldbalance(A) = -1 - max(h_{c}, h_{d}) + h_{d}$
$= -1 + max(h_{d}-h_{c},0)$
$= -1 + max(-oldbalance(B),0)$
$= -1 - min(oldbalance(B),0)$
所以代码中先计算A的平衡因子，再计算B的平衡因子。