Burnside引理

定义

    设G={a1,a2,…ag}是目标集[1,n]上的置换群。每个置换都写成不相交循环的乘积。c1(ak) 是在置换ak的作用下不动点的个数，也就是长度为1的循环的个数。G将[1,n]划分成l个等价类，则： 等价类个数为： 

      

相关知识

群  （这一段是百度上抄的。我才高一，个人认为现在看不懂很正常。）

给定一个集合G={a,b,c,…}和集合G上的二元运算，并满足:

(a) 封闭性："a,bÎG,$cÎG, a*b=c。

(b) 结合律："a,b,cÎG, (a*b)*c=a*(b*c)。

(c) 单位元：$eÎG,"aÎG, a*e=e*a=a。

(d) 逆元："aÎG,$bÎG, a*b=b*a=e，记b=a-1。

则称集合G在运算*之下是一个群，简称G是群。一般a*b简写为ab。

置换

n个元素1,2,…,n之间的一个置换表示1被1到n中的某个数a1取代，2被1到n中的某个数a2取代，直到n被1到n中的某个数an取代，且a1,a2,…,an互不相同。

置换群

置换群的元素是置换，运算是置换的连接。例如可以验证置换群满足群的四个条件。

例子

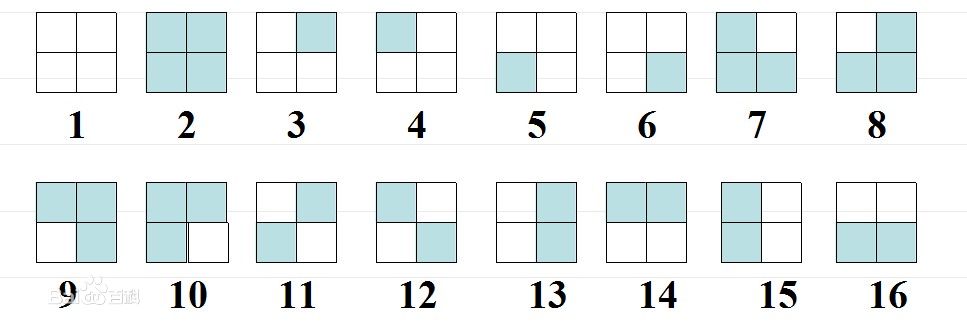
例：一正方形分成4格，2着色，有多少种方案？其中，经过转动相同的图象算同一方案。

解：每个格子一共有两种颜色可以选择，所以共有右图16中图像。

对图中图像的置换可以分为以下四种：

不动：a1=(1)(2)…(16)

逆时针转90度 ：a2=(1)(2)(3 4 5 6)(7 8 9 10) (11 12)(13 14 15 16)

顺时针转90度 ：a3=(1)(2)(6 5 4 3)(10 9 8 7)(11 12)(16 15 14 13)

转180度：a4=(1)(2)(3 5)(4 6)(7 9)(8 10)(11)(12) (13 15)(14 16)

由Burnside引理，共有(16+2+2+4)/4=6(种方案)

由例子可见，Burnsid引理是针对图像集的转动群来求解，当多种颜色着色时，理论上可以用Burnside来求解，但是极其复杂，此时一般通过Pólya定理求解（具体关于Pólya定理的问题之后的文章中会讲）。

Burnsid引理是群论中的一个公式，bzoj 1004 cards好像就可以用。