群论-Burnside引理与Polya定理 三千字

前言

网上各大OJ题解以及CSDN大部分博客把群论搞得神乎其神，从晦涩难懂毫无头绪的定义来理解群论是非常错误的。实际上群论并没有那么可怕

本博客从最简单的概念入手，没有长篇大论的证明，照样可以理解群论。

置换的概念：元素位置发生特定变化

1,2,3,4变换之后变成了3,2,4,1

不动点 若在置换时，某元素位置并不改变，则称该元素为该置换的不动点

公式：Burnside引理

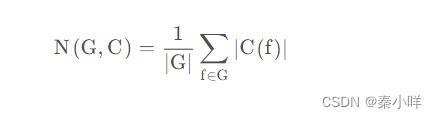
Burnside引理文字表述

对于一个置换f，若一个元素s经过该置换后不变，则称s为f的不动点，记f不动点个数为C(f),则（置换群）所有（方案数）置换等价类个数为所有C(f)的平均值

白话表述

方案数等于每个置换不动点个数的平均值

（其实我不解为什么几乎全部博客宁愿把这一句话论证几千字也不愿意说出来这一句白话）

例题

2 × 2 方格中每个格子可以选择染上 红色或者不染色。
现在要问，如果 不旋转、顺时针旋转 90 度、逆时针旋转 90  度、旋转 180 度后相同的均算成同一种方案，问总共有多少种不同的方案。

 得到四种置换 

f1=不旋转

f2=顺时针旋转90

f3=逆时针旋转90

f4=旋转180度

不动点个数

得到

 

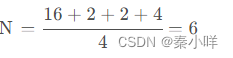
 一个3 × 3 的方格，用 10 种颜色给每个格子染色，旋转 0 度、顺时针旋转 90  度、旋转 180  度、逆时针旋转 90 度后，相同的均算成同一种方案，问总共有多少种不同的方案。

四个置换

f1=不旋转

f2=顺时针旋转90

f3=逆时针旋转90

f4=旋转180度

C(f1)  显然每个点都不变，每个点都有10种，共10^9

C(f2) （ 1 3 9 7 ）（ 2 4 6 8 ）（   5  ）想要旋转90度后，整体不变，那么1=3=9=7,2=4=6=8,5=5

共10*10*10种

C(f3)同理

C(f4) 1-9 3-7 2-8 4-6 5 五个集合必须满足相同 10^5种

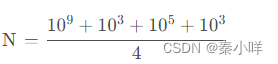
 Polya定理

循环节：循环的个数

故循环节为3

Polya定理

C(f)=k^(cnt)  cnt为循环节，即循环个数，k为染色数

所以得出白话结论  方案数等于所有置换f的的平均数

 

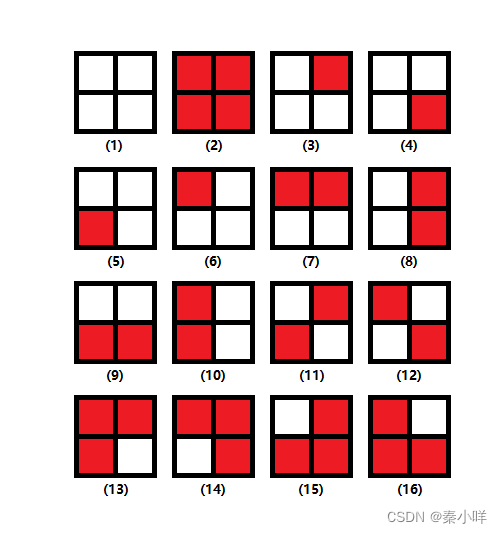
 给四个格子编号1234，得到以下循环表示

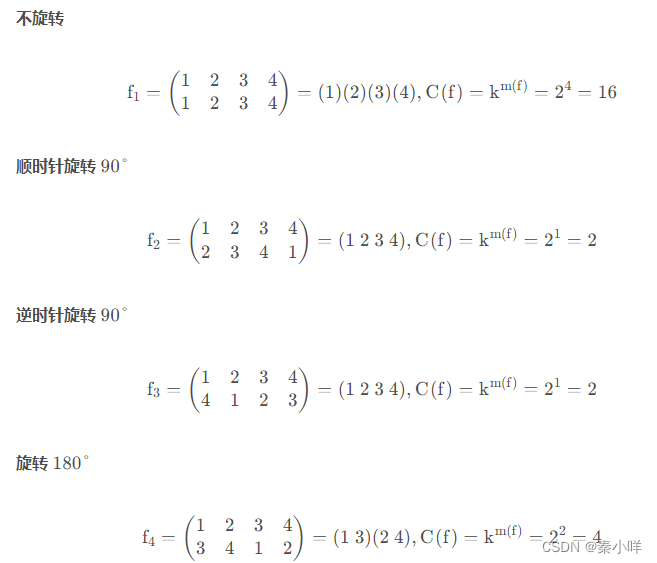
经典模式(以下ans应该除以对应的置换数）

旋转同构

一个置换，n个点，每个点移动k步，循环个数是gcd(k,n)

其中旋转k步的k在0-n-1之间

若有m个颜色

那么总方案数 

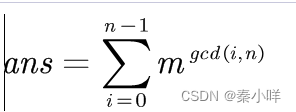
对称同构

包含翻转同构，旋转同构

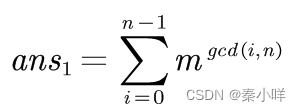
奇数个点时，对称轴有n条，长度为2的循环（翻转轴两侧必须相同）有(n-1)/2,长度为1的，对称轴穿过点有1个，共计(n+1)/2个循环，有n个置换,m种颜色，故

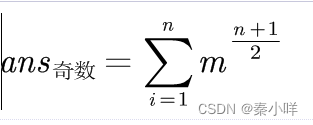
 偶数个点时，有过两点对称轴和不过点对称轴两种，前者n/2个置换，每个置换包含(n/2+1)个循环(   (n-2)/2+2 )，这里的+2代表是两个循环长度为1的循环，即被对称轴穿过，循环长度是1。

后者 n/2个置换，每个置换  n/2个循环。

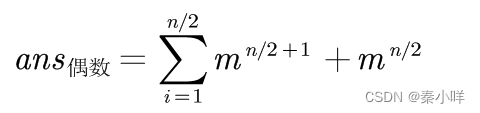
例题

Necklace of Beads

# include<iostream>

# include<algorithm>

using namespace std;

# define mod 1000000007
typedef long long int ll;

ll pow(int x)
{

    ll ans=1;

    for(int i=1; i<=x; i++)
    {
        ans*=3ll;
    }

    return ans;

}
int main ()
{

    ll n;

    cin>>n;

    ll ans=0;

    //旋转,3^gcd(9,n)

    for(ll i=0; i<=n-1; i++)
    {
        ans+=pow(__gcd(i,n));

    }



    if(n&1)
    {
        ll p=n/2+1;
        ans+=pow(p)*n;
    }
    else
    {

        ll p=n/2+1;
        ans+=pow(p)*n/2;
        ans+=pow(p-1)*n/2;

    }

    cout<<ans/(2*n);



    return 0;

}

例题一

【模板】Pólya 定理 - 洛谷

Color 注意取模超时

典型的旋转同构

推导如下

最后就是欧拉函数求解了，由于n范围大无法进行筛法求解，只能暴力求解，复杂度也是可以的

# include<iostream>
using namespace std;

# define mod 1000000007
typedef long long int ll;
ll fac[10000];

int len;

void init(ll x)
{
    len=0;

    for(ll i=1;i*i<=x;i++)
    {
        if(x%i==0)
        {
            fac[len]=i;

            len++;
            if(i*i!=x)
            {

                fac[len]=x/i;

                len++;

            }

        }
    }


}

ll getoula(ll x)
{
    ll ans=x;

    for(ll i=2;i*i<=x;i++)
    {
        if(x%i==0)
        {
            while(x%i==0)
            {

                x/=i;
            }

            ans=ans*(i-1)/i%mod;
        }
    }

    if(x>1)
    {
        ans=ans*(x-1)/x%mod;

    }

    return ans;

}

ll qp(ll base,ll pow)
{
    ll ans=1;

    while(pow)
    {
        if(pow&1)
            ans=ans*base%mod;

        pow>>=1;

        base=base*base%mod;

    }

    return ans;

}
int main ()
{

    int t;

    cin>>t;

    while(t--)
    {
        ll n;

        cin>>n;

        init(n);

        ll ans=0;

        for(int i=0;i<len;i++)
        {
            ans=(ans+qp(n,fac[i])*getoula(n/fac[i])%mod)%mod;
        }

        cout<<ans*qp(n,mod-2)%mod<<endl;

    }


    return 0;

}

Magic Bracelet

Magic Bracelet-【群论】【Burnside引理】【矩阵快速幂】_秦小咩的博客-CSDN博客

远山的占卜

转化的思想，将对角线两个元素看成一个元素，比较抽象，这样颜色就成了(m+1)*(m)/2种，然后是基本的循环置换，polya求解即可。

要注意的是  m变化之后必须取模，否则Wa的死死的 

# include<iostream>
# include<cstring>

# define mod  19260817

using namespace std;

typedef long long int  ll;

ll qp(ll base,ll pow)
{
    ll ans=1;

    while(pow)
    {
        if(pow&1)
            ans=base*ans%mod;
        pow>>=1;

        base=base*base%mod;
    }
    return ans;

}

int  prime[19260817+10];
int phi[19260817+10];

bool not_prime[19260817+10];

int tot;

void init()
{
    phi[1]=1;

    for(int i=2;i<=19260817+10;i++)
    {

        if(!not_prime[i])
        {
            tot++;

            prime[tot]=i;

            phi[i]=i-1;
        }

        for(int j=1;j<=tot&&(ll)(i*prime[j])<=19260817;j++)
        {


            not_prime[i*prime[j]]=1;

            if(i%prime[j]==0)
            {
                  phi[i*prime[j]]=(ll)prime[j]*phi[i]%mod;
                break;

            }

              phi[i*prime[j]]=(ll)(prime[j]-1)*phi[i]%mod;

        }
    }


}
int main ()
{


    int t;

    cin>>t;

    init();

    while(t--)
    {
        ll n,m;

        cin>>n>>m;

        m=m*(m+1)/2;

        ll ans=0;
        for(ll i=1;i*i<=n;i++)
        {
            if(n%i==0)
            {

                ans=(ans+(ll)phi[i]*qp(m,n/i)%mod)%mod;

                if(i*i!=n)
                {

                ans=(ans+(ll)phi[n/i]*qp(m,i)%mod)%mod;
                }
            }
        }

        cout<<ans*qp(n,mod-2)%mod<<endl;
    }

    return 0;
}