最近学了分治策略,基本步骤为:
- 分解:将问题分解为一些子问题,子问题和原问题形式一样,只是规模更小;
- 解决:求解出子问题,当规模足够小时,则停止递归,直接求解;
- 合并:将足问题的解合成原问题的解。
求最大子数组(mid为n/2),则最大子数组有三种情况:
- 全部位于mid左边;
- 全部位于mid右边;
- 经过mid的子数组。
暴力求解:即按顺序,从左至右进行求最大和,i=0 to n-1and j=i to n-1 ,比较求得最大值,那么算法复杂度很明显是O(n^2);这里不多说。
分治求解:
- 分解:mid=n/2;原问题分解成求mid左边最大子数组和求mid右边最大子数组;
- 解决:分解的同时已求得左右最大子数组,再去求经过mid的最大子数组,最后比较三种情况的最大值;
- 合并:从递归到规模最小,逐层合并求得最大子数组。
下面上代码:求解工具类:
public class ArrayUtil {
public static int actionCount=0; //计算运算次数,以度量算法复杂度
/*
* 暴力求解
*/
public static MaxArray getMaxArrayInForce(int[] arr){
int first=0;
int last=0;
actionCount=0;
if(arr.length==0)
return null;
MaxArray maxArray = new MaxArray();
int maxSum=arr[0];
for(int i=0;i<arr.length;i++){ //开始暴力求解
int sum=0;
for(int j=i;j<arr.length;j++){
sum+=arr[j];
actionCount++;
if(maxSum<sum){
maxSum=sum;
first=i;
last=j;
}
}
}
int[] resultArr=new int[last-first+1];
int cur=0;
for(int i = first;i<=last;i++){ //数组赋值
resultArr[cur++]=arr[i];
actionCount++;
}
maxArray.setSum(maxSum);
maxArray.setFirst(first);
maxArray.setLast(last);
maxArray.setArray(resultArr);
return maxArray;
}
/*
* 分治策略求解
*/
public static MaxArray getMaxArrayInDivide(int[] arr) {
if(arr.length==0)
return null;
ArrayResult arrayResult=getMaxSub(arr,0,arr.length-1);
MaxArray maxArray=new MaxArray();
maxArray.setSum(arrayResult.sum);
maxArray.setFirst(arrayResult.low);
maxArray.setLast(arrayResult.high);
int[] myArr=new int[maxArray.last-maxArray.first+1];
for(int i=maxArray.first;i<=maxArray.last;i++){
myArr[i-maxArray.first]=arr[i];
actionCount++;
}
maxArray.setArray(myArr);
return maxArray;
}
/*
* 递归求解最大子数组
*/
public static ArrayResult getMaxSub(int[] array ,int low,int high ){
if(high==low){ //递归的最小规模
ArrayResult result=new ArrayResult();
result.high=high;
result.low=low;
result.sum=array[low];
return result;
}
else{
int mid=(high+low)/2;
ArrayResult leftResult=getMaxSub(array, low, mid); //左递归
ArrayResult rightResult=getMaxSub(array, mid+1, high); //右递归
ArrayResult crossResult=getMaxCrossSub(array, low, high, mid); //求中间
if(leftResult.sum>=rightResult.sum&&leftResult.sum>=crossResult.sum)
return leftResult;
else if(rightResult.sum>=leftResult.sum&&rightResult.sum>=crossResult.sum)
return rightResult;
else
return crossResult;
}
}
/*
* 求经过中间的最大子数组
*/
private static ArrayResult getMaxCrossSub(int[] array ,int low,int high,int mid) {
int leftSum=array[mid];
int sum=0;
ArrayResult result=new ArrayResult();
for(int i=mid;i>=low;i--){ //求经过mid左边的最大子数组
actionCount++;
sum+=array[i];
if(sum>leftSum){
leftSum=sum;
result.low=i;
}
}
int rightSum=array[mid+1];
sum=0;
for(int j=mid+1;j<=high;j++){ //求经过mid右边的最大子数组
actionCount++;
sum+=array[j];
if(sum>rightSum){
rightSum=sum;
result.high=j;
}
}
result.sum=rightSum+leftSum; //合并左右
return result;
}
public static class ArrayResult{ //要用static类,因为static函数不能调用动态类(第88行)
int low=0; //而内部类用于将返回值打包起来
int high=0;
int sum=0;
}
}
存储类:
public class MaxArray {
int first=0;
int last=0;
int sum;
int[] array=null;
/**
* @return the first
*/
public int getFirst() {
return first;
}
/**
* @param first the first to set
*/
public void setFirst(int first) {
this.first = first;
}
/**
* @return the last
*/
public int getLast() {
return last;
}
/**
* @param last the last to set
*/
public void setLast(int last) {
this.last = last;
}
/**
* @return the array
*/
public int[] getArray() {
return array;
}
/**
* @param array the array to set
*/
public void setArray(int[] array) {
this.array = array;
}
/**
* @return the sum
*/
public int getSum() {
return sum;
}
/**
* @param sum the sum to set
*/
public void setSum(int sum) {
this.sum = sum;
}
}
下面是测试类:
public class Test {
public static void main(String[] args) {
int[] testArr={27,45,1,-5,-5,7,-4,-3,8,-15,19,-12,-14};
//MaxArray maxArray=ArrayUtil.getMaxArrayInForce(testArr); //暴力求解
MaxArray maxArray=ArrayUtil.getMaxArrayInDivide(testArr); //分治策略求解
int[] resultArr=maxArray.getArray();
System.out.println("最大子数组为第"+maxArray.first+1+"至第"+(maxArray.last+1)+"个数的数组");
System.out.println("最大子数组为:");
for(int i=0;i<resultArr.length;i++){
System.out.print(resultArr[i]+" ");
}
System.out.println();
System.out.println("最大子数组的和为:"+maxArray.sum);
System.out.println("操作次数:"+ArrayUtil.actionCount);
}
}
测试结果:
暴力求解:
分治求解:
完毕!








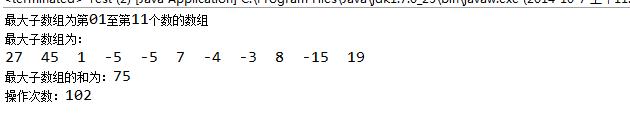















 2353
2353

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








