本内容主要来自我的一位学长YB收集的资料(有可能是他自己整理的资料),我就是通过他的资料才了解到并查集的强大和神奇之处,在此先对我的这位学长表示感谢。所以好东西就应该拿来分享。所以在此写出来希望对别人有所帮助。
尊重版权,转载请注明出处。
并查集是 一种数据结构,在acm中用的比较多。就想它名字所表达的那样,并查集就是一种 通常用来出来不相交集合 合并 和 查询的数据结构。
举个最常见的例子:
若某个家族人员过于庞大,要判断两个是否是亲戚,确实还很不容易,现在给出某个亲戚关系图,求任意给出的两个人是否具有亲戚关系。
规定:x和y是亲戚,y和z是亲戚,那么x和z也是亲戚。如果x,y是亲戚,那么x的亲戚都是y的亲戚,y的亲戚也都是x的亲戚。
数据输入:
第一行:三个整数n,m,p,(n<=20000,m<=1000000,p<=1000000),分别表示有n个人,m个亲戚关系,询问p对亲戚关系。
以下m行:每行两个数Mi,Mj,1<=Mi,Mj<=N,表示Ai和Bi具有亲戚关系。
接下来p行:每行两个数Pi,Pj,询问Pi和Pj是否具有亲戚关系。
数据输出:
P行,每行一个’Yes’或’No’。表示第i个询问的答案为“具有”或“不具有”亲戚关系。
样例:
input.txt
6 5 3
1 2
1 5
3 4
5 2
1 3
1 4
2 3
5 6
output.txt
Yes
Yes
No
通常这种问题的数据范围都很大,有一般的方法在时间效率上都会消耗很大。
所以 我们不妨把每个人都抽象成一个集合。
如:
初始时: {1},{2},{3},{4},{5},{6}
1-2是亲戚:{1,2},{3},{4},{5},{6}
1-5是亲戚:{1,2,5},{3},{4},{6}
3-4是亲戚:{1,2,5},{3,4},{6}
5-2是亲戚:{1,2,5},{3,4},{6}
1-3是亲戚:{1,2,3,4,5},{6}
于是判断两个人是否是亲戚时,简单的判断两个人是否的属于同一个集合就可以了。
很容易想到可以用染色法:
初始时:
1-2是亲戚:
1-5是亲戚:
3-4是亲戚:
5-2是亲戚:
1-3是亲戚:{1},{2}, {3},{4}, {5},{6}
对于合并过程,我们并不关心集合的具体颜色,因为对于任意的查询,我们只需要判断两个集合是否同色即可。
当然,在用代码实现时,染色法通常被体现为标记法,例如我们可以用数字1表示红色,数字2表示橙色……
容易发现,我们最多进行O(n)次染色,但每次染色时,必须遍历所有元素,这需要花费O(n)的时间。于是,总时间复杂度为O(n2+m+p),还是无法满足时间限制。
上述算法的瓶颈在于:无法快速的将同一集合的所有元素重新染色。
引入并查集:我们用b[i]表示元素i所在的集合(或者说元素i的颜色)。
仔细观察下面的过程,
初始时: b[1]=1,b[2]=2,b[3]=3,b[4]=4,b[5]=5,b[6]=6
1-2亲戚: b[1]=1,b[2]=1,b[3]=3,b[4]=4,b[5]=5,b[6]=6
1-5亲戚: b[1]=1,b[2]=1,b[3]=3,b[4]=4,b[5]=1,b[6]=6
3-4亲戚: b[1]=1,b[2]=1,b[3]=4,b[4]=3,b[5]=1,b[6]=6
5-2亲戚: b[1]=1,b[2]=1,b[3]=4,b[4]=3,b[5]=1,b[6]=6
1-3亲戚: b[1]=1,b[2]=1,b[3]=4,b[4]=1,b[5]=1,b[6]=6
将上述标记步骤体现为染色过程,
初始化:
1-2是亲戚:
1-5是亲戚:
3-4是亲戚:
5-2是亲戚:
1-3是亲戚:
对于上述的染色过程,前四步的染色和之前的染色法完全一致,但注意到第五步,我只将b[4]的标记(颜色)变成了1(红色),而对于和4在同一集合的3,并没有改变它的标记(颜色)b[4]=3(绿色)。
如果直接判断,因为{3}与集合{1,2,4,5}的颜色不同,因此会错误的认为,3和1,2,3,4,5不是亲戚。
实际上,在判断3与其它元素的关系时,我们并不关注3此时的颜色,而是去观察4的颜色,因为3此时颜色实际上是代表元素4(注意元素4一开始是绿色的)。
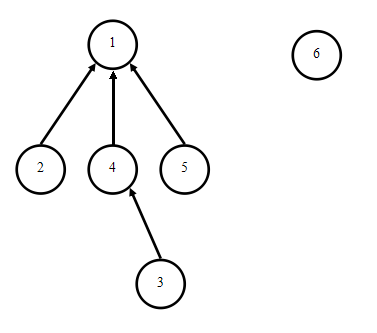
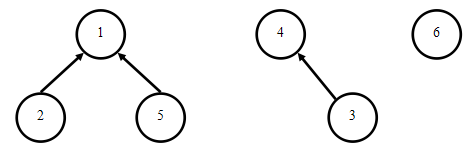
这样的描述可能难以理解,不妨回到最初的标记数组b[]中,观察b[]最终的状态:b[1]=1,b[2]=1,b[3]=4,b[4]=1,b[5]=1,b[6]=6。如果将b[i]理解为i的前驱(父节点),那么我们可以得到如下的树型关系图(森林):
于是,判断两元素是否属于同一集合等价于判断两元素是否处于同一棵树中。而集合的合并,对应的过程就是树的合并。
那么对于样例:
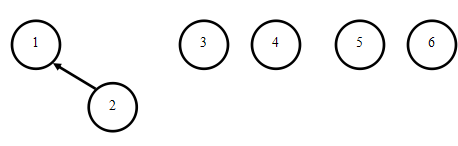
初始化:
1-2是亲戚:
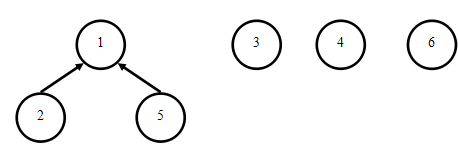
1-5是亲戚:
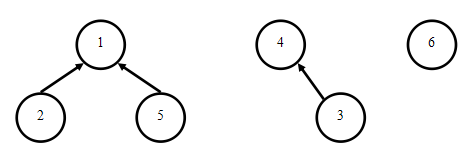
3-4是亲戚:(3指向4也是一样的)
5-2是亲戚:(已经在同一棵树中,不需改变)
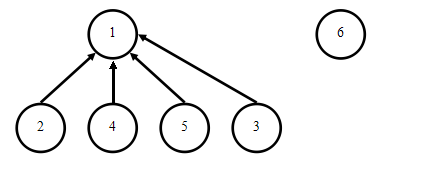
1-3是亲戚:(把4指向1的时候,3的根节点也就是1了。)
那么,如何快速判断两个元素x与y是否属于同一棵树呢?
我们只需要判断x的根节点与y的根节点是否相同即可,注意:这里指的是根节点,而不是父节点,因为对于任意的树形结构,根节点的是唯一确定的,它可以作为集合的标志(可以理解为集合的标记颜色)。
并且,在合并两棵树时,为了不造成子节点的丢失,我们并须将树的根进行合并。例如对于上述过程的最后一步:1和3是亲戚,我们是将3的根节点4并在另一个集合的根节点1中,而不是直接将3并在另一个集合中。
于是,我们得到了并查集的两种一般操作:
int find (int x){ //查询x所在的根节点编号。
while (x!=bleg[x])
x=bleg[x];
return x;
}
合并:
void Union (int a,int b){ //把a所在的数和b所在的树合并成一棵树。
int pa=find(a),pb=find(b);
if (pa!=pb) bleg[pa]=pb; //a所在的树成为b所在树的子树。
}
两种操作的代码都非常的简单,但执行的时间效率并不是很高。因为在节点很多的情况下,很容易造成树形结构的退化,
例如 对于样例:
判断5和3的关系,对于Find(5)而言,只需要执行一次while循环便可以找到根节点1。对于Find(3)而言,需要执行两次while循环才能找到根节点1。对于3的首次查询而言,的确必须花费o(2)的时间查询它的根节点,但如果需要对3进行反复询问,花费o(2)的时间就显得没必要了,因为我们已经知道了3所属的根节点是1,并且我们并不关心3原来的父节点是谁。因此,我们不妨在执行完查询操作后,把3的父节点直接更改为1。
于是,在执行完Find(3)后,树型结构变为:
经过这样的结构变更,在集合{1,2,3,4,5}没有改变之前(即没有新的合并操作),Find(3)的代价总是o(1)。
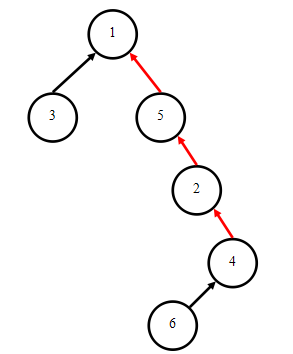
更一般的,对于如下的树型结构,右子树已经有退化成线性的趋势:
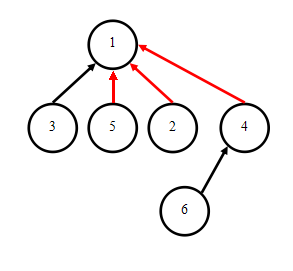
于是,在执行Find(4)时,我们可以把树型结构做如下变更:
可以发现,这样的结构变更是正确的,并且非常有必要。
这种树型结构的变更其实只是将某次查询中,将经过路径(对应红色的边)中的所有点,直接连接到根节点之下。
这种优化,通常称为路径压缩,给出加入优化后的Find操作:
int find (int x){
int y=x;
while (y!=bleg[y]) //先找到x的根节点
y=bleg[y];
while (x!=bleg[x]){ //对找x的根节点时经过的节点直接指向跟节点
int px=bleg[x];
bleg[x]=y;
x=px;
}
return y;
}
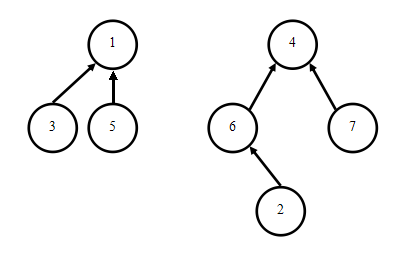
对于合并操作的优化:在合并下面两个集合(树)时,
将1 合并到4好还是将4合并到1好??
显然,通过图我们可以看到,以1为根节点的节点要 个数 小于以4为根节点的节点个数。A={1,3,5},B={1,4,6,7};
从概率学的角度出发,我们有理由相信,对于以4为根节点的树的查找要多于以1为根节点的树 。
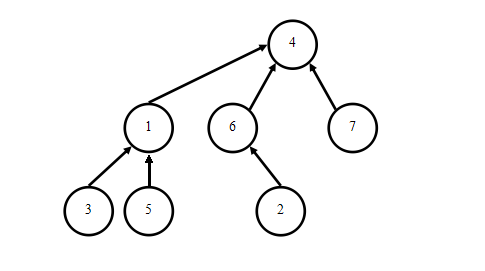
所以,我们不妨把集合A合并常到集合B中:
于是,我们有了一种启发式合并:记录每棵树的节点个数,对于每次合并,我们总是将节点个数少的树合并到节点个数多的树上。
我们用数组cnt[i]表示以i为根节点的树所拥有的节点个数,给出加入启发式合并的Union操作:
void Union (int a,int b){ /启发式合并操作
int pa=find(a),pb=find(b);
if (cnt[pa] < cnt[pb]){
bleg[pa]=pb;
cnt[pb] += cnt[pa];
}
else{
bleb[pb]=pa;
cnt[pa] += cnt[pb];
}
}
注意到,加入上述启发式合并后,大部分情况或者说在期望情况下,时间效率可以得到提高,但对于一些特殊的数据,时间效率甚至会降低。因此,我们还可以采取随机合并的方式代替启发式合并。
给出随机合并的Union操作:
void Union (int a,int b){
int pa=find (a),pb=find(b);
if (rand()%2)
bleg[pa]=pb;
else
bleg[pb]=pa;
}
入优化后的并查集,其时间效率接近线性,可以近似表示为O(n+m+p),已经可以轻松的面对题目所给的数据范围。
趁热打铁,尝试几道简单的并查集问题:



































 3560
3560











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








