首先子序列是指一个一个序列中,由若个数(字母)组成,然后从中任意删掉几个数(字母),保留剩下的数(字母)构成了一个序列,即称子序列。(或者从一个序列中,任意选取若干数或字符,按照这些数或字符原来的排序组成新的序列,即称子序列)
子串是指在一个字符串中任意选取连续的一段字符串,即称子串。
1首先看一下 最大子序列。
最大子序列是要找出由数组成的一维数组中和最大的连续子序列。比如{5,-3,4,2}的最大子序列就是 {5,-3,4,2},它的和是8,达到最大;而 {5,-6,4,2}的最大子序列是{4,2},它的和是6。你已经看出来了,找最大子序列的方法很简单,只要前i项的和还没有小于0那么子序列就一直向后扩展,否则丢弃之前的子序列开始新的子序列,同时我们要记下各个子序列的和,最后找到和最大的子序列。
def maxSumofSubArray(list):
if len(list) > 0:
max_sum = list[0]
pre_sum = 0
else:
max_sum = None
for i in list:
if pre_sum <0:
pre_sum = i
else:
pre_sum += i
if pre_sum > max_sum:
max_sum = pre_sum
return max_sum
def main():
list = [[6,-3,1,-2,7,-15,1,2,2],
[1, -2, 3, 10, -4, 7, 2, -5],
[1, 3, 10, -4, 7, 2],
[-2, -2, -1, -1, -2],
[-10, -3, -2, -14, 2],
[]]
for ls in list:
res = maxSumofSubArray(ls)
print('max sum of subarray is', res)
if __name__ == '__main__':
main()
参考博客:
最大子序列、最长递增子序列、最长公共子串、最长公共子序列、字符串编辑距离
2 最长递增子序列
最长递增子序列问题的描述:设L=<a1,a2,…,an>是n个不同的实数的序列,L的递增子序列是这样一个子序列Lin=<aK1,ak2,…,akm>,其中k1<k2<…<km且aK1<ak2<…<akm。求最大的m值。
这个问题可以转换为求这个序列与该序列排序后的序列之间的最长公共子序列。
设f(i)表示L中以ai为末元素的最长递增子序列的长度。则有如下的递推方程:
这个递推方程的意思是,在求以ai为末元素的最长递增子序列时,找到所有序号在L前面且小于ai的元素aj,即j<i且aj<ai。如果这样的元素存在,那么对所有aj,都有一个以aj为末元素的最长递增子序列的长度f(j),把其中最大的f(j)选出来,那么f(i)就等于最大的f(j)加上1,即以ai为末元素的最长递增子序列,等于以使f(j)最大的那个aj为末元素的递增子序列最末再加上ai;如果这样的元素不存在,那么ai自身构成一个长度为1的以ai为末元素的递增子序列。
L(i) = 1, i = 1或者不存在
A[j] < A[i] (1 <= j < i) = max(L(j) + 1) 所有下标为1 <= j < i中,存在A[j] < A[i]
def LIS(lis):
n = len(lis)
m = [1] * n
for i in range(n):
for j in range(i):
if lis[i] > lis[j] and m[i] < m[j] +1:
m[i] = m[j] +1
max_value = 0
for k in range(n):
# print(m[k])
if m[k] > max_value:
max_value = m[k]
return max_value
if __name__ == '__main__':
arr = [10, 22, 9, 33, 21, 50, 41, 60, 80]
print("最大递增子序列长度:", LIS(arr))3 最长公共子序列。
公共子序列 : 顾名思义,如果序列C既是序列A的子序列,同时也是序列B的子序列,则称它为序列A和序列B的公共子序列。
例如:对序列 1,3,5,4,2,6,8,7和序列 1,4,8,6,7,5 来说序列1,8,7是它们的一个公共子序列。请注意: 空序列是任何两个序列的公共子序列。例如: 序列1,2,3和序列4,5,6的公共子序列只有空序列。
最长公共子序列,A和B的公共子序列中长度最长的(包含元素最多的)叫做A和B的公共子序列。仍然用序列1,3,5,4,2,6,8,7和序列1,4,8,6,7,5它们的最长公共子序列是:1,4,8,7 / 1,4,6,7
最长公共子序列的长度是4 。请注意: 最长公共子序列不唯一。
最长公共子序列问题就是求序列A= a1,a2,……an, 和B = b1,b2,……bm,的一个最长公共子序列。
首先考虑暴力枚举:序列A有 2^n 个子序列,序列B有 2^m 个子序列,如果任意两个子序列一一比较,比较的子序列时间复杂度高达 2^(n+m) 。具体比较中对A中子序列需要检测是否是B的子序列,从而确定是否是AB的公共子序列,最后选出最长公共子序列,很明显不太现实。
进一步考量,只有长度相同的子序列才会真正进行比较。那么忽略空序列,我们来看看:对于A长度为1的子序列有C(n,1)个,长度为2的子序列有C(n,2)个,……长度为n的子序列有C(n,n)个。对于B也可以做类似分析,即使只对序列A和序列B长度相同的子序列做比较,那么总的比较次数高达:C(n,1)*C(m,1)*1 + C(n,2) * C(m,2) * 2+ …+C(n,p) * C(m,p)*p。其中p = min(m, n)。
也可以用递归的方法来解决
递归方法求最长公共子序列的长度
1)设有字符串a[0...n],b[0...m],下面就是递推公式。
当数组a和b对应位置字符相同时,则直接求解下一个位置;当不同时取两种情况中的较大数值。
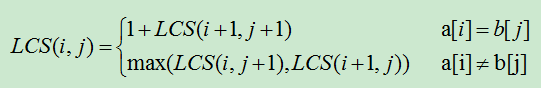
#!/usr/bin/env python
# -*- coding: utf-8 -*-
"""
递归方法求最长公共子序列的长度
1)设有字符串a[0...n],b[0...m],当数组a和b对应位置字符相同时,则直接求解下一个位置;当不同时取两种情况中的较大数值。
"""
def LCS2(i, j):
if i >= aLength or j >= bLength:
return 0
if aString[i] == bString[j]:
return 1 + LCS2(i+1,j+1)
else:
return LCS2(i + 1, j) if LCS2(i+1,j) > LCS2(i,j+1) else LCS2(i,j+1)
if __name__ == '__main__':
# aString = 'ABCBDAB'
# bString = 'BDCABA'
aString = "ABCBDAB"
bString = "BDCABA";
aLength = len(aString)
bLength = len(bString)
print('最长公共子序列长度为:', LCS2(0,0))
用递归的方法优点是编程简单,容易理解。缺点是效率不高,有大量的重复执行递归调用,而且只能求出最大公共子序列的长度,求不出具体的最大公共子序列。
动态规划求解
【问题】 求两字符序列的最长公共字符子序列
问题描述:字符序列的子序列是指从给定字符序列中随意地(不一定连续)去掉若干个字符(可能一个也不去掉)后所形成的字符序列。令给定的字符序列X=“x0,x1,…,xm-1”,序列Y=“y0,y1,…,yk-1”是X的子序列,存在X的一个严格递增下标序列<i0,i1,…,ik-1>,使得对所有的j=0,1,…,k-1,有xij=yj。例如,X=“ABCBDAB”,Y=“BCDB”是X的一个子序列。
考虑最长公共子序列问题如何分解成子问题,设A=“a0,a1,…,am-1”,B=“b0,b1,…,bm-1”,并Z=“z0,z1,…,zk-1”为它们的最长公共子序列。不难证明有以下性质:
(1) 如果am-1=bn-1,则zk-1=am-1=bn-1,且“z0,z1,…,zk-2”是“a0,a1,…,am-2”和“b0,b1,…,bn-2”的一个最长公共子序列;
(2) 如果am-1!=bn-1,则若zk-1!=am-1,蕴涵“z0,z1,…,zk-1”是“a0,a1,…,am-2”和“b0,b1,…,bn-1”的一个最长公共子序列;
(3) 如果am-1!=bn-1,则若zk-1!=bn-1,蕴涵“z0,z1,…,zk-1”是“a0,a1,…,am-1”和“b0,b1,…,bn-2”的一个最长公共子序列。
这样,在找A和B的公共子序列时,如有am-1=bn-1,则进一步解决一个子问题,找“a0,a1,…,am-2”和“b0,b1,…,bm-2”的一个最长公共子序列;如果am-1!=bn-1,则要解决两个子问题,找出“a0,a1,…,am-2”和“b0,b1,…,bn-1”的一个最长公共子序列和找出“a0,a1,…,am-1”和“b0,b1,…,bn-2”的一个最长公共子序列,再取两者中较长者作为A和B的最长公共子序列。
求解:
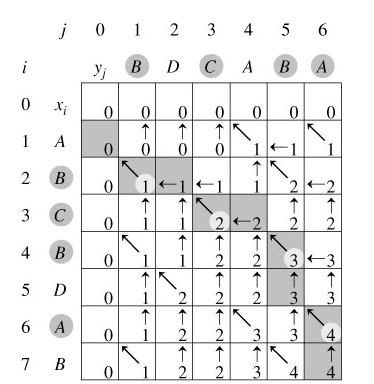
引进一个二维数组c[m][n],用c[i][j]记录X[i]与Y[j] 的LCS 的长度,b[i][j]记录c[i][j]是通过哪一个子问题的值求得的,以决定搜索的方向。
我们是自底向上进行递推计算,那么在计算c[i,j]之前,c[i-1][j-1],c[i-1][j]与c[i][j-1]均已计算出来。此时我们根据X[i] = Y[j]还是X[i] != Y[j],就可以计算出c[i][j]。
问题的递归式写成:
回溯输出最长公共子序列过程:
算法分析:
由于每次调用至少向上或向左(或向上向左同时)移动一步,故最多调用(m + n)次就会遇到i = 0或j = 0的情况,此时开始返回。返回时与递归调用时方向相反,步数相同,故算法时间复杂度为Θ(m + n)。
方向数组fMat是完全可以省略的:
数组元素c[i,j]的值仅由c[i-1,j-1],c[i-1,j]和c[i,j-1] 三个值之一确定,因此,在计算中,可以临时判 断c[i,j]的值是由c[i-1,j-1],c[i-1,j]和c[i,j-1]中哪一 个数值元素所确定,代价是Ο(1)时间。
若只计算LCS的长度,则空间复杂度为min(m, n)。
在计算c[i,j]时,只用到数组c的第i行和第i-1行。 因此,只要用2行的数组空间就可以计算出最长公 共子序列的长度。
#!/usr/bin/env python
# -*- coding: utf-8 -*-
"""
最长公共子序列
"""
def GetLCSLength(aString, bString, aLength, bLength):
cMat = [[0 for i in range(bLength+1)] for j in range(aLength+1)]
fMat = [[0 for i in range(bLength+1)] for j in range(aLength+1)]
for i in range(aLength):
for j in range(bLength):
if aString[i] == bString[j]:
cMat[i + 1][j + 1] = cMat[i][j] +1
fMat[i + 1][j + 1] = 'OK'
elif cMat[i + 1][j] > cMat[i][j + 1]:
cMat[i + 1][j + 1] = cMat[i + 1][j]
fMat[i + 1][j + 1] = 'Left'
else:
cMat[i + 1][j + 1] = cMat[i][j + 1]
fMat[i + 1][j + 1] = 'Up'
for i in cMat:
print(i)
print('')
for j in fMat:
print(j)
print('')
return cMat, fMat
def GetLCSString(aString, fMat, i, j):
if i == 0 or j == 0:
return
if fMat[i][j] == 'OK':
GetLCSString(aString, fMat, i-1, j-1)
print(aString[i-1],end='')
elif fMat[i][j] == 'Left':
GetLCSString(aString,fMat,i,j-1)
else:
GetLCSString(aString,fMat,i-1,j)
if __name__ == '__main__':
# aString = 'ABCBDAB'
# bString = 'BDCABA'
aString = "a1b2c3"
bString = "1a1wbz2c123a1b2c123";
aLength = len(aString)
bLength = len(bString)
cMat,fMat = GetLCSLength(aString, bString,aLength,bLength)
GetLCSString(aString, fMat, aLength, bLength)问题拓展:设A、B、C是三个长为n的字符串,它们取自同一常数大小的字母表。设计一个找出三个串的最长公共子序列的O(n^3)的时间算法。
思路:跟上面的求2个字符串的公共子序列是一样的思路,只不过这里需要动态申请一个三维的数组,三个字符串的尾字符不同的时候,考虑的情况多一些而已。
#!/usr/bin/env python
# -*- coding: utf-8 -*-
"""
寻找三个字符串的最长公共子串
"""
def max1(m, n):
return m if m > n else n
def max2(x, y, z, k, m, n):
max = -1
tmp = [x,y, z, k, m, n]
return max if max > sorted(tmp)[len(tmp)-1] else sorted(tmp)[len(tmp)-1]
def GetMLCSLength(str1, str2, str3):
# length1,length2,length3 = 3,3,2
length1, length2, length3 = len(str1), len(str2), len(str3)
print(length1, length2, length3 )
# 构建一个三维数组
c3Mat = []
for ii in range(length1 +1):
row = []
for jj in range(length2+1):
col = []
for kk in range(length3+1):
col.append(0)
row.append(col)
c3Mat.append(row)
for i in range(1,length1):
for j in range(1,length2):
for k in range(1,length3):
if str1[i] == str2[j] and str2[j] == str3[k]:
c3Mat[i + 1][j + 1][k + 1] = c3Mat[i][j][k] +1
elif str1[i] == str2[j] and str1[i] != str3[k]:
c3Mat[i + 1][j + 1][k + 1] = max1(c3Mat[i+1][j+1][k], c3Mat[i][j][k+1])
elif str1[i] == str3[k] and str1[i] != str2[j]:
c3Mat[i + 1][j + 1][k + 1] = max1(c3Mat[i+1][j][k+1], c3Mat[i][j+1][k])
elif str2[j] == str3[k] and str1[i] != str2[j]:
c3Mat[i + 1][j + 1][k + 1] = max1(c3Mat[i][j+1][k+1], c3Mat[i+1][j][k])
else:
c3Mat[i + 1][j + 1][k + 1] = max2(c3Mat[i][j+1][k+1],c3Mat[i+1][j][k+1],c3Mat[i+1][j+1][k],c3Mat[i][j][k+1],c3Mat[i][j+1][k],c3Mat[i+1][j][k])
length = c3Mat[length1][length2][length3]
return length
if __name__ == '__main__':
aString = 'ABCBDAB'
bString = 'BDCABA'
cString = 'FEBCBA'
length = GetMLCSLength(aString, bString,cString)
print("最长公共子序列的长度为:",length)
最小编辑距离
给定一个源串和目标串,能够对源串进行如下操作:
- 在给定位置上插入一个字符
- 替换任意字符
- 删除任意字符
写一个程序,返回最小操作数,使得对源串进行这些操作后等于目标串,源串和目标串的长度都小于2000。
分析与解法
此题常见的思路是动态规划,假如令dp[i][j] 表示源串S[0…i] 和目标串T[0…j] 的最短编辑距离,其边界:dp[0][j] = j,dp[i][0] = i,那么我们可以得出状态转移方程:
- dp[i][j] =min{
- dp[i-1][j] + 1 , S[i]不在T[0…j]中
- dp[i-1][j-1] + 1/0 , S[i]在T[j]
- dp[i][j-1] + 1 , S[i]在T[0…j-1]中
}
接下来,咱们重点解释下上述3个式子的含义
- 关于dp[i-1][j] + 1, s.t. s[i]不在T[0…j]中的说明
- s[i]没有落在T[0…j]中,即s[i]在中间的某一次编辑操作被删除了。因为删除操作没有前后相关性,不妨将其在第1次操作中删除。除首次操作时删除外,后续编辑操作是将长度为i-1的字符串,编辑成长度为j的字符串:即dp[i-1][j]。
- 因此:dp[i][j] = dp[i-1][j] + 1。
- 关于dp[i-1][j-1] + 0/1, s.t. s[i] 在T[j]的说明
- 若s[i]经过编辑,最终落在T[j]的位置。
- 则要么s[i] == t[j],s[i]直接落在T[j]。这种情况,编辑操作实际上是将长度为i-1的S’串,编辑成长度为j-1的T’串:即dp[i-1][j-1];
- 要么s[i] ≠ t[j],s[i] 落在T[j]后,要将s[i]修改成T[j],即在上一种情况的基础上,增加一次修改操作:即dp[i-1][j-1] + 1。
- 关于dp[i][j-1] + 1, s.t. s[i]在T[0…j-1]中的说明
- 若s[i]落在了T[1…j-1]的某个位置,不妨认为是k,因为最小编辑步数的定义,那么,在k+1到j-1的字符,必然是通过插入新字符完成的。因为共插入了(j-k)个字符,故编辑次数为(j-k)次。而字符串S[1…i]经过编辑,得到了T[1…k],编辑次数为dp[i][k]。故: dp[i][j] = dp[i][k] + (j-k)。
- 由于最后的(j-k)次是插入操作,可以讲(j-k)逐次规约到dp[i][k]中。即:dp[i][k]+(j-k)=dp[i][k+1] + (j-k-1) 规约到插入操作为1次,得到 dp[i][k]+(j-k) =dp[i][k+1] + (j-k-1) =dp[i][k+2] + (j-k-2)=… =dp[i][k+(j-k-1)] + (j-k)-(j-k-1) =dp[i][j-1] + 1。
上述的解释清晰规范,但为啥这样做呢?
换一个角度,其实就是字符串对齐的思路。例如把字符串“ALGORITHM”,变成“ALTRUISTIC”,那么把相关字符各自对齐后,如下图所示:
把图中上面的源串S[0…i] = “ALGORITHM”编辑成下面的目标串T[0…j] = “ALTRUISTIC”,我们枚举字符串S和T最后一个字符s[i]、t[j]对应四种情况:(字符-空白)(空白-字符)(字符-字符)(空白-空白)。
由于其中的(空白-空白)是多余的编辑操作。所以,事实上只存在以下3种情况:
- 下面的目标串空白,即S + 字符X,T + 空白,S变成T,意味着源串要删字符
- dp[i - 1, j] + 1
- 上面的源串空白,S + 空白,T + 字符,S变成T,最后,在S的最后插入“字符”,意味着源串要添加字符
- dp[i, j - 1] + 1
- 上面源串中的的字符跟下面目标串中的字符不一样,即S + 字符X,T + 字符Y,S变成T,意味着源串要修改字符
- dp[i - 1, j - 1] + (s[i] == t[j] ? 0 : 1)
综上,可以写出简单的DP状态方程:
//dp[i,j]表示表示源串S[0…i] 和目标串T[0…j] 的最短编辑距离
dp[i, j] = min { dp[i - 1, j] + 1, dp[i, j - 1] + 1, dp[i - 1, j - 1] + (s[i] == t[j] ? 0 : 1) }
//分别表示:删除1个,添加1个,替换1个(相同就不用替换)。#!/usr/bin/env python
# -*- coding: utf-8 -*-
"""
最小编辑距离
"""
def Edit_Distance(src, tar):
srcLength = len(src)
tarLength = len(tar)
matrix = [[i+j for j in range(tarLength + 1)] for i in range(srcLength + 1)]
for i in range(1,srcLength+1):
matrix[i][0] = i
for j in range(1,tarLength+1):
matrix[0][j] = j
for i in range(1,srcLength+1):
for j in range(1,tarLength+1):
if src[i-1] == tar[j-1]:
matrix[i][j] = matrix[i-1][j-1]
else:
matrix[i][j] =min(matrix[i-1][j-1] +1, 1+ min(matrix[i-1][j], matrix[i][j-1]))
for i in matrix:
print(i)
print(matrix[srcLength][tarLength])
return matrix[srcLength][tarLength]
if __name__ == "__main__":
# src = 'abddcdefdgbd22svb'
# tar = 'bcdefg34rdyvdfsd'
# src = 'ofailing'
# tar = 'osailn'
src = "string"
tar = "story"
Edit_Distance(src, tar)
以下为几种最小编辑距离算法的比较,其中函数(1)为调用数学工具包Numpy, 函数(2)和(1)算法类似,都是采用DP, (3)来自wiki(4)是直接调用python的第三方库Levenshtein
import time
from functools import wraps
import cProfile
import numpy
import Levenshtein
def fn_timer(function):
@wraps(function)
def function_timer(*args, **kwargs):
t0 = time.time()
result = function(*args, **kwargs)
t1 = time.time()
print("Total time running %s: %s seconds" % (function.__name__, str(t1 - t0)) )
return result
return function_timer
def levenshtein1(source, target):
if len(source) < len(target):
return levenshtein1(target, source)
if len(target) == 0:
return len(source)
# We call tuple() to force strings to be used as sequences
# ('c', 'a', 't', 's') - numpy uses them as values by default.
source = numpy.array(tuple(source))
target = numpy.array(tuple(target))
# We use a dynamic programming algorithm, but with the added optimization that we only
# need the last two rows of the matrix.
previous_row = numpy.arange(target.size + 1)
for s in source:
# Insertion (target grows longer than source):
current_row = previous_row + 1
# Substitution or matching:
# Target and source items are aligned, and either
# are different (cost of 1), or are the same (cost of 0).
current_row[1:] = numpy.minimum(
current_row[1:],
numpy.add(previous_row[:-1], target != s))
# Deletion (target grows shorter than source):
current_row[1:] = numpy.minimum(
current_row[1:],
current_row[0:-1] + 1)
previous_row = current_row
return previous_row[-1]
def levenshtein2(s1, s2):
if len(s1) < len(s2):
return levenshtein2(s2, s1)
if len(s2) == 0:
return len(s1)
previous_row = range(len(s2) + 1)
for i, c1 in enumerate(s1):
current_row = [i + 1]
for j, c2 in enumerate(s2):
insertions = previous_row[
j + 1] + 1 # j+1 instead of j since previous_row and current_row are one character longer
deletions = current_row[j] + 1 # than s2
substitutions = previous_row[j] + (c1 != c2)
current_row.append(min(insertions, deletions, substitutions))
previous_row = current_row
return previous_row[-1]
def levenshtein3(s, t):
''' From Wikipedia article; Iterative with two matrix rows. '''
if s == t:
return 0
elif len(s) == 0:
return len(t)
elif len(t) == 0:
return len(s)
v0 = [None] * (len(t) + 1)
v1 = [None] * (len(t) + 1)
for i in range(len(v0)):
v0[i] = i
for i in range(len(s)):
v1[0] = i + 1
for j in range(len(t)):
cost = 0 if s[i] == t[j] else 1
v1[j + 1] = min(v1[j] + 1, v0[j + 1] + 1, v0[j] + cost)
for j in range(len(v0)):
v0[j] = v1[j]
return v1[len(t)]
@fn_timer
def calllevenshtein1(s, t, n):
for i in range(n):
t1 = levenshtein1(s, t)
@fn_timer
def calllevenshtein2(s, t, n):
for i in range(n):
t2 = levenshtein2(s, t)
print(t2)
@fn_timer
def calllevenshtein3(s, t, n):
for i in range(n):
levenshtein3(s, t)
@fn_timer
def calllevenshtein4(s, t, n):
for i in range(n):
Levenshtein.distance(s, t)
if __name__ == "__main__":
n = 1
a = 'abddcdefdgbd22svb'
b = 'bcdefg34rdyvdfsd'
calllevenshtein1(a, b, n)
calllevenshtein2(a, b, n)
calllevenshtein3(a, b, n)
calllevenshtein4(a, b, n)








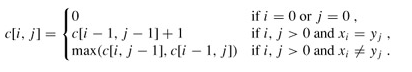














 1710
1710











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








