二分查找算法

        在计算机科学中，折半搜索，也称二分查找算法、二分搜索，是一种在有序数组中查找某一特定元素的搜索算法。假设待查数组是按升序排列的，搜素过程从数组的中间元素开始，如果中间元素正好是要查找的元素，则搜素过程结束；如果某一特定元素大于或者小于中间元素，则在数组大于或小于中间元素的那一半中查找，而且跟开始一样从中间元素开始比较。如果在某一步骤子数组为空，则代表找不到。这种搜索算法每一次比较都使搜索范围缩小一半。

折半搜索每次把搜索区域减少一半，时间复杂度为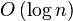。（n代表集合中元素的个数） 。优点是比较次数少，查找速度快，平均性能好。其缺点就是要求是个有序数组。

 

//假设数组是升序的

1.仅用循环搞定

int BinarySearch(int arr[], int low, int high, int key)
{
	int pos=-1; //查找到的位置.-1表示没有找到
	int mid; //区间的中间位置

	//在[low,high]区间查找等于key值的数据位置，采用二分思想，        
	//即先让[low,high]中间的元素arr[mid]与key比较，
	//如果相等的话，查找结束，说明这个位置就是要找的位置
	//如果大于key则说明可能要找的数据在[low,mid-1]区间里,在新区间继续查找
	//如果小于key，则说明可能要找的数据在[mid+1,high]区间里，在新区间继续查找
	//重复上述过程，如果区间为空时，即low==high+1, low>high，查找结束，此时说明查找失败。

	while(low<=high)       //区间为空停止查找
	{
		mid=(low+high)>>1;   //求[low,high]区间的中间位置mid

		if(arr[mid]==key)    //找到了要找的数,停止查找，位置为mid
		{
			pos=mid;
			break;
		}
		else if(arr[mid]>key) //可能要找的数据在[low,mid-1]中，更新high
			high=mid-1;
		else                 //可能要找的数据在[mid+1,high]中,更新low
			low=mid+1;
	}

	return pos;
}

2.用递归搞定

int BinarySearch(int arr[], int low, int high, int key)
{
	int pos=-1; //要找的位置，-1表示未找到

	if(low<=high) //区间不为空，则继续查找
	{
		int mid=(low+high)>>1;  //求出[low,high]区间的中间位置mid

		if(arr[mid]==key)      //说明找到了
			pos=mid;

		else if(arr[mid]>key)
			pos=BinarySearch(arr,low,mid-1); //在[low,mid-1]区间继续查找

		else 
			pos=BinarySearch(arr,mid+1,high); //在[mid+1,high]区间继续查找
	}

	return pos;
}