POJ1459Power Network（电网）——最大流水题

http://poj.org/problem?id=1459

长篇阅读。。。

题目描述：
一个电网包含一些结点（电站、消费者、调度站），这些结点通过电线连接。每个结点u 可能
被供给s(u)的电能，s(u)≥0；同时也可能产生p(u)的电能，0≤p(u)≤pmax(u)；站点u 还有可能
消费c(u)电能，0≤c(u)≤min( s(u), cmax(u) )；可能传输d(u)的电能，d(u) = s(u) + p(u) - c(u)。
以上这些量存在以下限制关系：对每个电站，c(u) = 0；对每个消费者，p(u) = 0；对每个调度站，
p(u) = c(u) = 0。
在电网中两个结点u 和v 之间最多有一条电线连接。从结点u 到结点v 传输L(u,v)的电能，0≤L(u,v)≤Lmax(u,v)。定义Con 为c(u)的总和，表示电网中消费电能的总和。本题的目的是求
Con 的最大值。
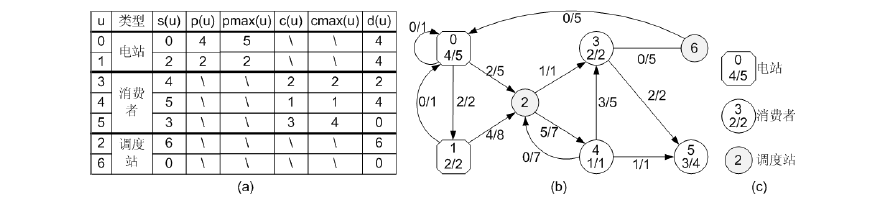
电网的一个例子如图6.24 所示。在图(a)中，电站结点u 的标记”x/y”代表p(u) = x、pmax(u) =
y。消费者结点u 的标记”x/y”代表c(u) = x、cmax(u) = y。每条电线所对应的边(u,v)，其标记”x/y”
代表L(u,v) = x、Lmax(u,v) = y。在图(b)中，消费的最大电能Con = 6，图(a)列出了在此状态下各
个站点的s(u)、p(u)、c(u)和d(u)。注意，如图(b)所示的电网中，电能的流动还存在其他状态，但
消费的电能总和不超过6。

输入描述：
输入文件中包含多个测试数据。每个测试数据描述了一个电网。每个测试数据的第1 行为4
个整数：n np nc m，其中，0≤n≤100，代表结点数目；0≤np≤n，代表电站数目；0≤nc≤n，
代表消费者数目；0≤m≤n2，代表传输电线的数目。接下来有m 个三元组，(u,v)z，其中u 和v
为结点序号（结点序号从0 开始计起），0≤z≤1000，代表Lmax(u,v)的值。接下来有np 个二元
组，(u)z，其中u 为电站结点的序号，0≤z≤10000，代表pmax(u)的值；每个测试数据的最后是
nc 个二元组，(u)z，其中u 为消费者结点的序号，0≤z≤10000，代表cmax(u)的值。所有数据
都是整数。除三元组(u,v)z 和二元组(u)z 中不含空格外，输入文件中其他位置允许出现空格。测试
数据一直到文件尾。

输出描述：
对输入文件中每个测试数据所描述的电网，输出占一行，为一个整数，表示电网中能消费电
能的最大值。

原图中的电站，消费者不能作为源点和汇点，添加一个源点和汇点，源点到电站的容量为pmax，消费者到汇点的容量为cmax，则原题就转化为求解最大流了
题目的输入用正则表达式sscanf(s,”(%d,%d)%d”,&u,&v,&z);
ISAP…
Memory: 1060K Time: 110MS

#include<iostream>
#include<cstring>
#include<cstdio>
#include<vector>
const int maxn=110;
const int maxm=1010;
const int INF=0x3f3f3f3f;
using namespace std;
int n,s,t;
struct Edge{
    int from,to,cap,flow;
    Edge(int u,int v,int c,int f):from(u),to(v),cap(c),flow(f){}
};
vector<Edge> edges;
vector<int> G[maxn];
int gap[maxn],d[maxn],cur[maxn],p[maxn];
inline void addedge(int u,int v,int c){
    edges.push_back(Edge(u,v,c,0));
    edges.push_back(Edge(v,u,0,0));
    int m=edges.size();
    G[u].push_back(m-2);
    G[v].push_back(m-1);
}
int ISAP(){
    s=n,t=n+1;
    n+=2;
    memset(cur,0,sizeof(cur));
    memset(d,0,sizeof(d));
    memset(gap,0,sizeof(gap));
    int x=s,flow=0,a=INF;
    while(d[s]<n){
        if(x==t){
            flow+=a;
            while(x!=s){
                edges[p[x]].flow+=a;
                edges[p[x]^1].flow-=a;
                x=edges[p[x]].from;
            }
            a=INF;
        }
        int ok=0;
        for(int i=cur[x];i<G[x].size();++i){
            Edge& e=edges[G[x][i]];
            if(e.cap>e.flow&&d[e.to]+1==d[x]){
                p[e.to]=G[x][i];
                cur[x]=i;
                x=e.to;
                ok=1;
                a=min(a,e.cap-e.flow);
                break;
            }
        }
        if(!ok){
            int m=n;
            for(int i=0;i<G[x].size();++i){
                Edge& e =edges[G[x][i]];
                if(e.cap>e.flow) m=min(m,d[e.to]);
            }
            if(--gap[d[x]]==0) break;
            gap[d[x]=m+1]++;
            cur[x]=0;
            if(x!=s) x=edges[p[x]].from;
        }
    }
    return flow;
}
void Init(){
    edges.clear();
    for(int i=0;i<maxn;++i) G[i].clear();
}
int main()
{
    int np,nc,m;
    while(scanf("%d%d%d%d",&n,&np,&nc,&m)!=EOF){
        Init();
        int u,v,z;
        char s[10];
        for(int i=0;i<m;++i){
            scanf("%s",s);sscanf(s,"(%d,%d)%d",&u,&v,&z);
            addedge(u,v,z);
        }
        for(int i=0;i<np;++i){
            scanf("%s",s);
            sscanf(s,"(%d)%d",&u,&z);
            addedge(n,u,z);
        }
        for(int i=0;i<nc;++i){
            scanf("%s",s);
            sscanf(s,"(%d)%d",&u,&z);
            addedge(u,n+1,z);
        }
        int ans=ISAP();
        cout<<ans<<endl;
    }
    return 0;
}