Codeforces Round #299 (Div. 2)——A.B.C.D

http://codeforces.com/contest/535

A. Tavas and Nafas
题目描述：给你0~99的数字，输出它的英文表示法

#include<bits/stdc++.h>
using namespace std;
char* s[100]={
"zero","one","two","three","four","five","six","seven","eight","nine",
"ten","eleven", "twelve","thirteen","fourteen","fifteen","sixteen", "seventeen",
"eighteen","nineteen","twenty","thirty","forty","fifty","sixty","seventy",
"eighty","ninety"};
int main()
{
    int n;
    scanf("%d",&n);
    if(n<=20) puts(s[n]);
    else{
        int a=n%10;
        int b=n/10;
        if(a!=0)
            printf("%s-%s\n",s[20+b-2],s[a]);
        else puts(s[20+b-2]);
    }
    return 0;
}

B. Tavas and SaDDas
题目描述：
一个数只含4和7为幸运数，给你一个幸运数，判断该数在幸运数序列中的位置

分析：
可以用一个队列算出所有的幸运数或者打表
队列是这样的：先把4,7入队；然后取出对头x，将x*10+4和x*10+7放入队列

或者：

#include<bits/stdc++.h>
using  namespace std;
int main()
{
    char s[11];
    scanf("%s",s);
    int l=strlen(s);
    int res=1;
    for(int i=0;i<l;++i){
        res*=2;
        if(s[i]=='7') res+=1;
    }
    printf("%d\n",res-1);
    return 0;
}

C. Tavas and Karafs
题目描述：
给定一个等差数列，进行t次操作，每次选择m个数，使得这m个数减1.问t次操作后从左端点l开始最长的0序列的右端点为多少

分析：
假设右端点为r,
则max(hl,hl+1,hl+2,…,hr)<=t&&(hl+  hl + 1 + …,+ hr)<=t*m
二分枚举可能的最大右端点，判断可行性

#include<bits/stdc++.h>
#define ll long long
const int MAXN=100010;
using namespace std;
ll a,b,n;
ll calc(int k)
{
    return (ll)a+(k-1)*b;
}
ll sum(int x,int y)
{
    return (calc(x)+calc(y))*(y-x+1)/2;
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("in.cpp","r",stdin);
#endif // ONLINE_JUDGE
    ll l,t,m;
    scanf("%I64d%I64d%I64d",&a,&b,&n);
    while(n--) {
        scanf("%I64d%I64d%I64d",&l,&t,&m);
        if(calc(l)>t) puts("-1");
        else {
            ll L=l,R=(t-a)/b+1,mid;
            while(L<=R) {
                mid=L+(R-L)/2;
                if(sum(l,mid)<=(ll)t*m) L=mid+1;
                else R=mid-1;
            }
            printf("%I64d\n",L-1);
        }
    }
    return 0;
}

D. Tavas and Malekas
题目描述：
有一个原串的长度为n，给一个字串s，然后给出m个字串出现的位置
求原串可能有多少种
6 2
ioi
1 3
那么由s串构成的原串为“ioioi_” 有一个空位置，则原串的种类为26^1

分析：
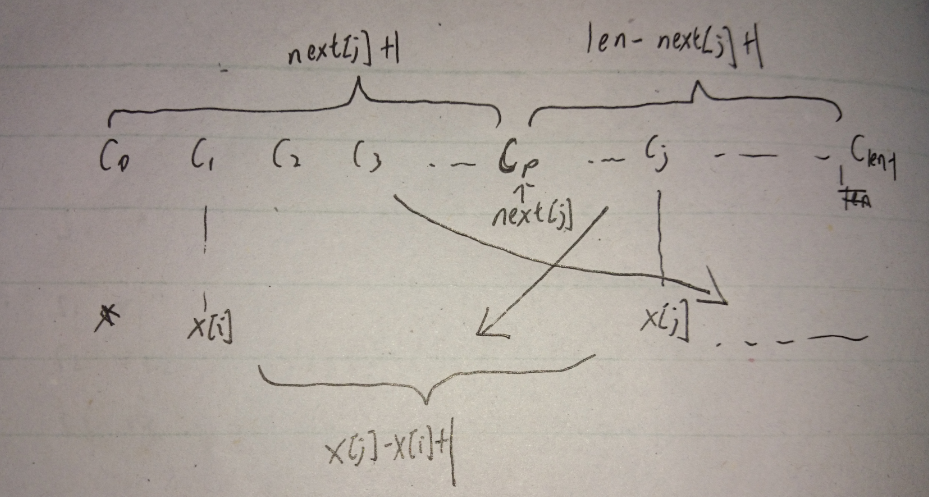
假设s串为abababab
两个位置xi,xj 要使得这两个位置合法那么xj前半部分的字符和xi后半部分的字符必须相同
怎么快速判断是否相同？毕竟m，n为1e6
KMP,那么(xj-xi+1)=(len-next[j]+1)

#include<bits/stdc++.h>
typedef long long ll;
const int MAXN=1000010;
const ll mod=1000000007ll;
using namespace std;
int n,m;
int Next[MAXN],x[MAXN];
char s[MAXN];
map<int,int> mp;
int len;
void get_Next(){
    Next[0]=-1;
    int i=0,j=-1;
    while(i<len){
        if(j==-1||s[i]==s[j]) Next[++i]=++j;
        else j=Next[j];
    }
}
ll pow(ll a,int b){
    ll ans=1;
    for(;b;b>>=1){
        if(b&1){
            ans*=a;
            ans%=mod;
        }
        a*=a;a%=mod;
    }
    return ans;
}
ll solve(){
    if(m==0) return pow(26ll,n);
    ll res=pow(26ll,x[1]-1);
    for(int i=2;i<=m;++i){
        if(x[i]-x[i-1]>=len){
            res*=pow(26ll,x[i]-x[i-1]-len);
            res%=mod;
        }
        else{
            if(!mp.count(x[i]-x[i-1]+1)) return 0;
        }
    }
    res*=pow(26ll,n-x[m]-len+1);
    res%=mod;
    return res;
}

int main()
{
#ifndef ONLINE_JUDGE
freopen("in.cpp","r",stdin);
#endif // ONLINE_JUDGE
    scanf("%d%d",&n,&m);
    scanf("%s",s);
    for(int i=1;i<=m;++i) scanf("%d",&x[i]);
    len=strlen(s);
    get_Next();
    int i=len;
    mp.clear();
    while(Next[i]!=0){
        mp[len-Next[i]+1]=1;
        i=Next[i];
    }
    printf("%I64d\n",solve());
    return 0;
}