数据结构4.1——树

树(tree)

  （定义树的一种自然的方式是递归的方法）一棵树是一些节点的集合。这个集合可以是空集；若非空，则一棵树是由称作根（root)的节点r以及0个或多个非空的子树T1，T2......TK组成。

  

    度（Degree)：结点拥有的 子树数称为结点的度。

    叶子(Leaf)或终端结点：度为0的结点。

    非终端结点或分支结点:度不为0的结点。

    树的度：树内各结点的度的最大值。

    结点的子树的根称为该结点的 孩子，相应的，该结点称为该孩子的 双亲。

    深度：树中结点的最大层次称为树的深度。

    如果将树中结点的各子树看成从左至右是有次序的，则称该树为 有序树，否则称为 无序树。

    森林：m棵互不相交的树的集合。

   

树的存储结构

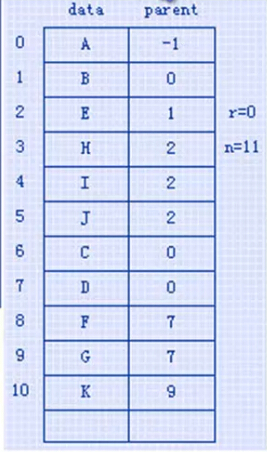
1.双亲表示法

以一组连续空间存储树的结点，同时在每个结点中，附设一个指示器指示其双亲结点在数组中的位置。

typedef struct treeNode
{
	int data;
	int parent;
}treeNode;

typedef struct tree
{
	treeNode nodes[MAX_TREE_SIZE];
	int root,n;//根的位置和结点数目；
}tree;

当要知道结点的孩子时，需要遍历整个树的结构，可以附设一个域来表示其第一个孩子的坐标或者表示其右兄弟的位置。

2.孩子表示法

可以为每个结点设计多个指针域，其中每个指针指向一颗子树的根结点。

一种方法是将指针域的个数设为树的度（如图）。

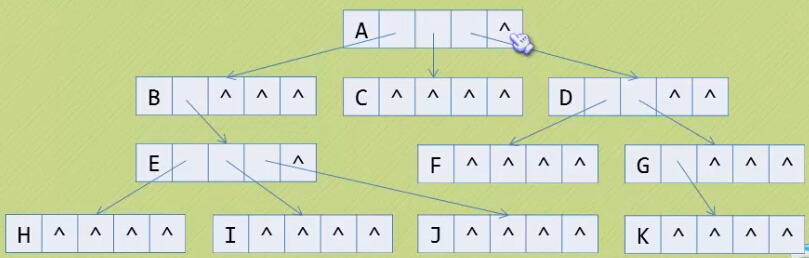
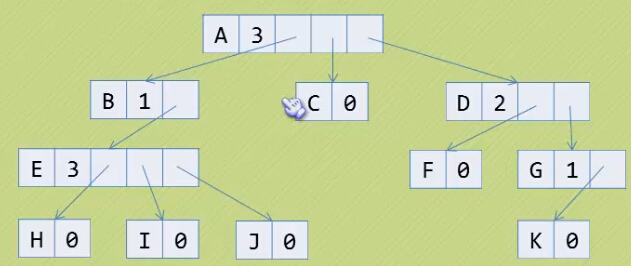
另一种方法，是附设一个数据表示需要的指针的个数（如图）

还有一种更好的方法，把每个结点的孩子结点排列起来以单链表作为存储结构。则n个结点就有n个孩子链表，如果是叶子结点，则该链表为空。

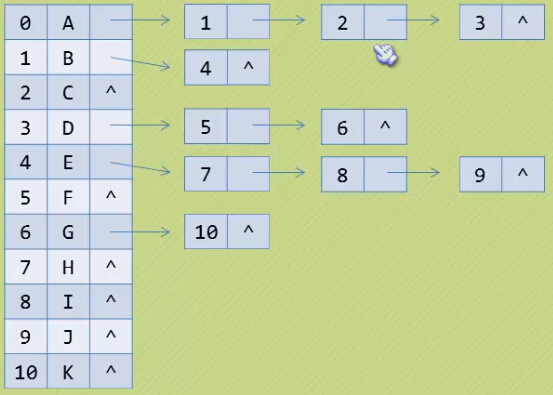
typedef struct chileNode//孩子结点
{
	int child;
	struct childNode *next;
}*childPtr;

typedef struct rootNode//表所记录的根结点
{
	int data;
	childPtr *firstChild;
}rootNode;

typedef struct tree//树结构
{
	rootNode nodes[MAX_TREE_SIZE];//结点数组
	int root,n;//根的位置和结点数目；
}tree;

还可以附设一个域表示其双亲的位置，这样不仅可以知道孩子的位置，还可以知道其双亲的位置（孩子双亲表示法）。

3.孩子兄弟表示法

任意一棵树，它的结点的第一个孩子如果存在就是唯一的，它的右兄弟如果存在也是唯一的，可以设置两个指针，分别指向该结点的第一个孩子和此节点的右兄弟。

typedef struct treeNode
{
	int data;
	struct treeNode *firstchild,*rightsib;/* data */
}treeNode,*treePtr;

二叉树

     每个结点至多有两颗子树（不存在度大于2的结点），二叉树的子树有左右之分，其次序不能任意颠倒。

    

    二叉树的性质：

• 在二叉树的i层上至多有2^(i-1)个结点（i>=1)
• 深度为k的二叉树至多有2^k-1个结点（k>=1)
• 对任何一颗二叉树T，如果其终端结点数为n0,度为2的节点数为n2,则n0 = n2 +1

满二叉树

   一颗深度为k的二叉树有2^k-1个结点的二叉树称为满二叉树。

完全二叉树

    深度为k的，有n个节点的二叉树，当且仅当其每一个点都与深度为k的满二叉树中编号从1至n的结点一一对应时，称为完全二叉树。

    具有n个结点的完全二叉树的深度为[log2^n]+1；

    叶子结点只能出现在最下面两层；

    最下层的叶子一定集中在左部连续位置；

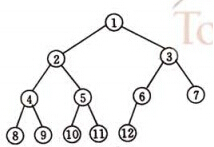
二叉树的存储结构

     1. 顺序存储结构

         用一组地址连续的存储单元依次自上而下、自左至右存储完全二叉树上的结点元素。    

      2.链式存储结构

         二叉树的结点由一个数据元素和分别指向其左、右子树的两个分支构成，则表示二叉树的 链表中的结点至少包括三个域：数据域和左右指针域。 

typedef struct BiNode
{
	chat data;
	struct BiNode *lchild,*rchild;
}BiNode,*BiTree;

遍历二叉树

      

     从根节点出发，按照某种次序依次访问二叉树中所有结点，使得每个结点被访问一次且仅被访问一次。

     先序遍历 DLR 中序遍历 LDR 后序遍历 LRD

    

      先序遍历二叉树：
           若树为空，则空操作，否则：
           访问根节点；先序遍历左子树；先序遍历右子树。 
      中序遍历二叉树：
           若树为空，则空操作，否则：
           中序遍历左子树；访问根节点；中序遍历右子树。 
      后序遍历二叉树：
           若树为空，则空操作，否则：
           后序遍历左子树；后序遍历右子树；访问根节点； 

typedef struct BiNode
{
	chat data;
	struct BiNode *lchild,*rchild;
}BiNode,*BiTree;

//前序遍历二叉树

void preOrderTraverse(BiTree T)
{
	if(NULL==T)
		return;
	printf("%c",T->data);
	preOrderTraverse(T->lchild);
	preOrderTraverse(T->rchild);
}

//前序遍历创建二叉树
void creatTree(BiTree *tree)//传入指向指针的指针才能修改指针的值
{
	char c;
	scanf("%c",&c);

	if(' '==c)
	{
		*tree=NULL ;
	}
	else
	{
		*tree=(BiTree)malloc(sizeof(BiNode));
		(*tree)->data=c;
		creatTree(&(*tree)->lchild);
		creatTree(&(*tree)->rchild);		
	}
	return;
}