多项式拟合,模型的复杂度以及权重的变化

1.1多项式拟合

生成目标数据

目标数据集的生成方式:

• 首先计算函数sin (2πx) 的对应的值
• 然后给每个点增加一个小的符合高斯分布的随机噪声
• 通过使用这种方式产生数据,它们拥有一个内在的规律,这个规律是我们想要学习的。同时也包含随即噪声，这种噪声可能由随机的过程产生，也可能是由于存在没有被观察到的具有变化性的噪声源。

训练数据和测试数据:

• 训练数据用来训练多项式模型,来学习数据中的规律
• 测试数据,测试模型在新数据上的泛化能力(测试集由100个数据点组成,这100个数据点的生成方式与训练集的生成方式完全相同,但是在目标值中包含的随机噪声的值不同.)

1.2数据可视化:

• 10 个数据点组成的训练集的图像,用蓝色圆圈标记.
• 100 个数据点组成的测试数据集,用黄色的圆圈标记.
• 红色曲线给出了用来生成数据的sin (2πx) 函数.
• 我们的目标是对于某些新的 x 值,预测 y 的值.

1.3 多项式函数拟合

$$f(x,w)=w_0+w_{1}x+w_2{x}^2+...+w_M{x}^M=\sum _{j=0}^M{w}_j{x}^j$$

• $M$ : 多项式的阶数
• $w$ : 代表系数向量, $w_0,w_2,w_3,....w_m$

1.4 误差函数

• 误差函数衡量了对于任意给定的 $w$ 值,函数 $f(x,w)$ 与训练集数据目标值的差别。

$$E(w)=\frac{1}{2}\sum _{i=1}^N(f(x_i,w)-y{)}^2$$

• $w$ : 系数向量,通过最小化误差函数来确定
• $f(x,w)$ : 从数据中学习得到的函数
• $\frac{1}{2}$ : 系数为了方便计算
• $N$ : 样本的数量

1.5 多项式特征

例如，如果输入样本是二维的并且形式为$[a，b]$，则2次多项式特征是$[1，a，b，a^2，ab，b^2]$。

sklearn,提供了多项式特征的方法:

from sklearn.preprocessing import PolynomialFeatures

X = np.arange(6).reshape(3, 2)

poly = PolynomialFeatures(2)
poly.fit_transform(X)

>>> array([[ 1.,  0.,  1.,  0.,  0.,  1.],
          [ 1.,  2.,  3.,  4.,  6.,  9.],
          [ 1.,  4.,  5., 16., 20., 25.]])

1.6 LinearRegression拟合多项式特征

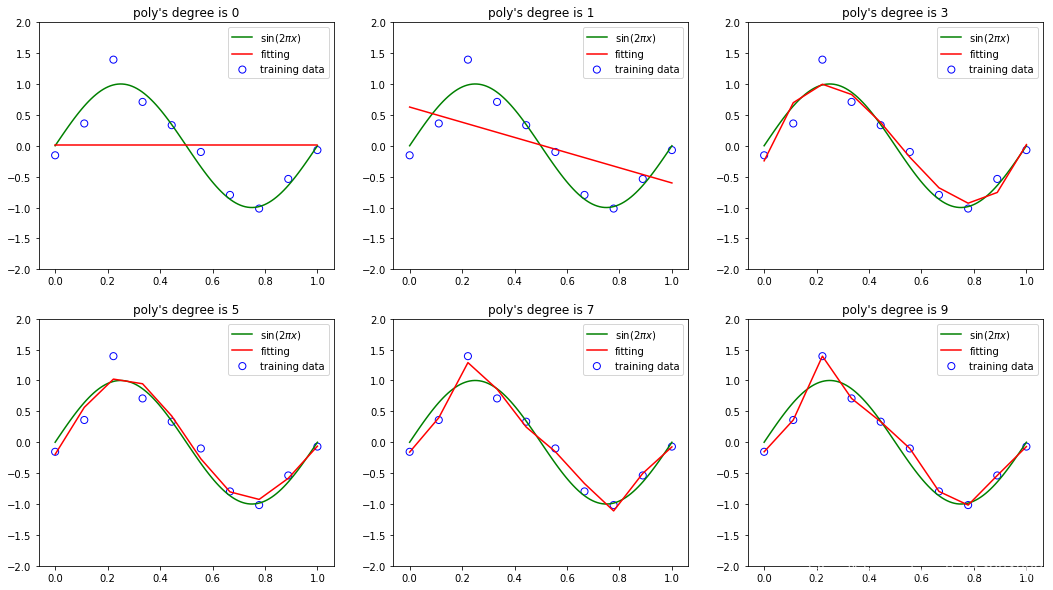
1.6.1 拟合结果

• ( M = 0 )和一阶( M = 1 )多项式对于数据的拟合效果相当差
• 三阶( M = 3 )多项式似乎给出了对函数sin (2πx) 的最好的拟合
• 当我们达到更高阶的多项式( M = 9 ),我们得到了对于训练数据的一个完美的拟合事实上,$E(w^{\ast })=0$。
• 高阶多项式特征虽然完美拟合,然而,但是,拟合的曲线剧烈震荡,就表达函数sin (2πx) 而言表现很差。
• 图四这种行为叫做过拟合( over-fitting )

1.7 测试

测试:通过对新数据的预测情况判断模型($f(x,w)$)的泛化性。

测试的方式为:

• 通过一个额外的测试集,这个测试集由100个数据点组成,这100个数据点的生成方式与训练集的生成方式完全相同,但是在目标值中包含的随机噪声的值不同。我们可以定量考察模型的泛化性与 M(阶数) 的关系,对于每个 M ,计算测试集的 $E(w)$ 。

有时候使用根均方(RMS)误差更方便。这个误差由下式定义:
$$E_{rms}=\sqrt{\frac{2E(w^{\ast })}{N}}$$

• N : (样本点的数量)以相同的基础对比不同大小的数据集,
• 平方根确保了$E_{rms}$与目标变量$y$使用相同的规模和单位进行度量。
  　

学习曲线

1.7.1 测试结果

• M(阶数)过大过小都会造成测试误差很大
• 当 M 的取值为 3 ≤ M ≤ 6 时,测试误差较小

1.8 不同阶多项式的系数

	0	1	2	3	4	5	6	7	8	9
0	0.0	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
1	0.0	-1.438176	-0.985530	12.997090	17.383902	5.641664	-0.256404	1.924420	-4.560926	-215.451195
2	0.0	0.000000	-0.452646	-37.304887	-59.458286	38.420548	111.186592	75.201286	205.987591	5077.185412
3	0.0	0.000000	0.000000	24.568161	60.101335	-216.569502	-529.761376	-316.364404	-1302.830510	-45179.500599
4	0.0	0.000000	0.000000	0.000000	-17.766587	299.360835	904.596578	301.203617	4022.592501	210149.339158
5	0.0	0.000000	0.000000	0.000000	0.000000	-126.850969	-665.218737	214.704064	-7532.869930	-569098.691158
6	0.0	0.000000	0.000000	0.000000	0.000000	0.000000	179.455923	-459.109693	8579.726633	928109.751580
7	0.0	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	182.447319	-5351.534105	-897238.544636
8	0.0	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	1383.495356	473256.605051
9	0.0	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	-104860.691043

系数分析:

• 对于 M = 9,训练集的误差为0,此时的多项式函数有10个自由度,对应于10个系数$w_0,...w_9$,所以可以调节模型的参数,使得模型与训练集中的10个数据点精确匹配。
• 因为高阶多项式包含了所有低阶的多项式函数作为特殊情况。 M = 9 的多项式因此能够产生至少与 M = 3 一样好的结果。
• 随着 M 的增大,系数的大小通常会变大。对于 M = 9 的多项式,通过调节系数,让系数取相当大的正数或者负数,多项式函数可以精确地与数据匹配,但是对于数据之间的点(尤其是临近区间端点处的点),函数表现出剧烈的震荡。直觉上讲,发生了这样的事情:有着更大的 M 值的更灵活的多项式被过分地调参,使得多项式被调节成了与目标值的随机噪声相符。

1.9 曾加训练数据的数量

• 给定同样的阶数(即模型的复杂度)
• 对比在相同阶数和测试数据下,不同规模数据上模型的泛化情况
• 红色模型的拟合曲线

增加训练数据.10倍,100倍

不同量级训练集对模型权重的影响

　

1.9.1结果分析

• 给定的模型复杂度,当数据集的规模增加时,过拟合问题减弱
• 数据集规模越大,我们能够用来拟合数据的模型就越复杂(即越灵活)
• 数据点的数量不应该小于模型的可调节参数的数量的若干倍(比如5或10)
• 因此,我们需要根据训练数据的规模来限制模型的复杂度(即参数的数量),根据待解决的问题的复杂性来选择模型的复杂性

1.10 正则化(regularization)

• 正则化是一种控制过拟合现象的技术(即可以在不限制模型复杂度的情况下,降低过拟合)
• 一般给误差函数增加一个惩罚项,使得系数不会达到很大的值(减小系数的值)

增加L2正则项后的误差函数

$$E^{}(w)=\frac{1}{2}\sum _{i=1}^N(f(x,w)-y{)}^2+\frac{\lambda }{2}\parallel w^2\parallel$$

• $\parallel w^2\parallel =w_0^2+w_1^2+w_2^2+....w_M^2$
• $\lambda$ : 控制正则化的程度,$\lambda$越大,$w$的值越小.
• 注意,通常系数$w_0$从正则化项中省略

不同正则化系数对模型泛化效果的影

．．．未完待续