经典背包问题（装船问题）C++版

大家对背包问题想必都比较了解了，就是在限制重量的前提下使得装入的物品价值最大，当然各物品都有自己的重量和价值。

该题目有两个限制条件，一是不能超重，二是总价值最大。

这就要求在装包时既要考虑价值最大化又要防止超重，可以理解为物品重量和价值的综合体。那就可以考虑用价值和重量的比值作为一个参考，而且是最合理的指标，我们的目的是在不超重的前提下总价值最大，当然最理想的情况便是装入重量轻价值大的物品。

我们把物品重量和价值的比称为绝对比，通过排序最后将绝对比大的先装入背包，依次便可实现目的。

以下是算法的大体步骤：

1.先定义三个数组分别存储物品的重量、价值和绝对比，分别命名为wei，pri和rat，数组大小为物品的数量，可自行设置。

2.键盘输入限定的总重量，并依次输入物品的重量和价值，根据两个数组的数据求得绝对比放入rat数组。

3.对rat数组的元素进行排序（降序），同时调整wei和pri数组，因为最后三者要保持一致。

4.排好序后分别输出三个数组的元素，判定条件为wei数组的总重量不高于限定值，这样便可以实现问题的最优解。最后可以得出装入背包总价值、总重量以及物品数。

上代码：

#include<iostream>
using namespace std;
const int N=5;
int main()
{
	double wei[N];
	double pri[N];
	double rat[N];
	int i,j,k;
	double m;
	cout<<"请输入背包的最大载重量："<<endl;
	cin>>m;
	cout<<"请输入各物品的重量和价值："<<endl;
	for(i=0;i<N;i++)  cin>>wei[i]>>pri[i];
	cout<<"各个物品的绝对比为："<<endl;
    for(i=0;i<N;i++)  rat[i]=pri[i]/wei[i];
	for(j=0;j<=N-2;j++)
		for(k=0;k<=N-2-j;k++)
		{
			double tempRat,tempPri,tempWei;
			if(rat[k]<rat[k+1])
			{
				tempWei=wei[k];
				wei[k]=wei[k+1];
				wei[k+1]=tempWei;//交换物品的重量；

				tempPri=pri[k];
				pri[k]=pri[k+1];
				pri[k+1]=tempPri;//交换物品的价值；

				tempRat=rat[k];
				rat[k]=rat[k+1];
				rat[k+1]=tempRat;//交换物品的绝对比；

			}
		}
	cout<<"按照绝对比降序排列后的物品重量数组为："<<endl;
	for(i=0;i<N;i++)   cout<<wei[i]<<",";
	cout<<endl;
    cout<<"按照绝对比降序排列后的物品价值数组为："<<endl;
	for(i=0;i<N;i++)   cout<<pri[i]<<",";
	cout<<endl;
	cout<<"绝对比数组为："<<endl;
	for(i=0;i<N;i++)   cout<<rat[i]<<",";
	cout<<endl;

	int count=0;
	double sumWei=0.0,sumPri=0.0;
	while((sumWei+wei[count])<=m&&count<N)
	{
		sumWei=sumWei+wei[count];
		sumPri=sumPri+pri[count];
		count++;
	}
	cout<<"背包的总重量为："<<sumWei<<endl;
	cout<<"背包的总价值为："<<sumPri<<endl;
	cout<<"背包的物品数量为："<<count<<endl;

	return 0;


}

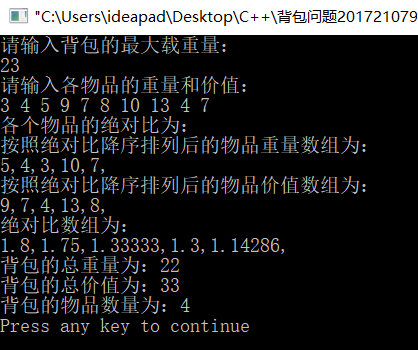
编译之后结果如下：