C++背包问题（01、多重、完全）

#include<stdio.h>
#define N 5 //物品数量
#define M 10 //背包容量
#define max(a,b) a>=b?a:b
int dp1[N+1][M+1];
int dp2[N+1][M+1];
int dp3[N+1][M+1];
int dpp[M+1];
int w[] = {0,2,2,6,5,4};  //体积
int v[] = {0,6,3,5,4,6};  //价值
int s[] = {0,2,3,4,2,2};  //数量

//0-1背包（物品只有一个）
int Bag_01(){
    int i,j;
    for(i=1;i<=N;i++)
        for(j=1;j<=M;j++){
            dp1[i][j] = dp1[i-1][j];
            if(j>=w[i])
                dp1[i][j] = max(dp1[i-1][j],dp1[i-1][j-w[i]]+v[i]);
        }
    return dp1[N][M];
}

//多重背包（物品有限个）
int Bag_02(){
    int i,j,k;
    for(i=1;i<=N;i++)
        for(j=1;j<=M;j++)
            for(k=0;k<=s[i] && j>=k*w[i];k++)
                dp2[i][j] = max(dp2[i][j],dp2[i-1][j-k*w[i]]+k*v[i]);
    return dp2[N][M];
}

//完全背包（物品不限个）---二维数组
int Bag_031(){
    int i,j;
    for(i=1;i<=N;i++)
        for(j=1;j<=M;j++){
            dp3[i][j] = dp3[i-1][j];
            if(j>=w[i]&&dp3[i][j]<dp3[i][j-w[i]]+v[i])
                dp3[i][j] = dp3[i][j-w[i]]+v[i];
        }
    return dp3[N][M];
}

//完全背包（物品不限个）---一维数组
int Bag_032(){
    int i,j;
    for(i=1;i<=N;i++)
        for(j=w[i];j<=M;j++)
            dpp[j]=max(dpp[j],dpp[j-w[i]]+v[i]);
    return dpp[M];
}

int main(){
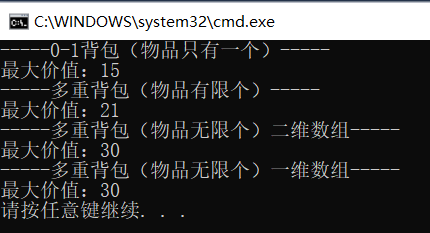
    printf("-----0-1背包（物品只有一个）-----\n");
    printf("最大价值：%d\n",Bag_01());
    printf("-----多重背包（物品有限个）-----\n");
    printf("最大价值：%d\n",Bag_02());
    printf("-----多重背包（物品无限个）二维数组-----\n");
    printf("最大价值：%d\n",Bag_031());
    printf("-----多重背包（物品无限个）一维数组-----\n");
    printf("最大价值：%d\n",Bag_032());
}