《Batch Normalization Accelerating Deep Network Training by Reducing Internal Covariate Shift》阅读与理解_batch nomalization:accelerating deep network train-CSDN博客

《Batch Normalization Accelerating Deep Network Training by Reducing Internal Covariate Shift》是google的一篇关于批处理的文章，详细的介绍了使用BN的具体优势

一、神经网络中的权重初始化与预处理方法的关系

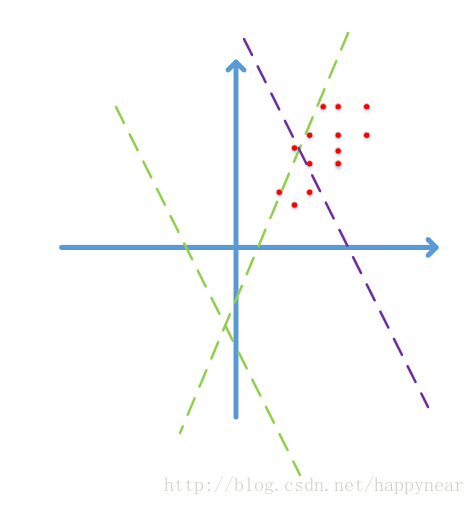
如果做过dnn的实验，大家可能会发现在对数据进行预处理，例如白化或者zscore，甚至是简单的减均值操作都是可以加速收敛的，例如下图所示的一个简单的例子：

　　图中红点代表2维的数据点，由于图像数据的每一维一般都是0-255之间的数字，因此数据点只会落在第一象限，而且图像数据具有很强的相关性，比如第一个灰度值为30，比较黑，那它旁边的一个像素值一般不会超过100，否则给人的感觉就像噪声一样。由于强相关性，数据点仅会落在第一象限的很小的区域中，形成类似上图所示的狭长分布。

　　而神经网络模型在初始化的时候，权重W是随机采样生成的，一个常见的神经元表示为：ReLU(Wx+b) = max(Wx+b,0)，即在Wx+b=0的两侧，对数据采用不同的操作方法。具体到ReLU就是一侧收缩，一侧保持不变。

　　随机的Wx+b=0表现为上图中的随机虚线，注意到，两条绿色虚线实际上并没有什么意义，在使用梯度下降时，可能需要很多次迭代才会使这些虚线对数据点进行有效的分割，就像紫色虚线那样，这势必会带来求解速率变慢的问题。更何况，我们这只是个二维的演示，数据占据四个象限中的一个，如果是几百、几千、上万维呢？而且数据在第一象限中也只是占了很小的一部分区域而已，可想而知不对数据进行预处理带来了多少运算资源的浪费，而且大量的数据外分割面在迭代时很可能会在刚进入数据中时就遇到了一个局部最优，导致overfit的问题。

　　这时，如果我们将数据减去其均值，数据点就不再只分布在第一象限，这时一个随机分界面落入数据分布的概率增加了多少呢？2^n倍！如果我们使用去除相关性的算法，例如PCA和ZCA白化，数据不再是一个狭长的分布，随机分界面有效的概率就又大大增加了。

　　不过计算协方差矩阵的特征值太耗时也太耗空间，我们一般最多只用到z-score处理，即每一维度减去自身均值，再除以自身标准差，这样能使数据点在每维上具有相似的宽度，可以起到一定的增大数据分布范围，进而使更多随机分界面有意义的作用。

二、Batch Normalization

Batch Normalization（BN）的动机

一般来说，如果模型的输入特征不相关且满足标准正态分布 N(0, 1)

时，模型的表现一般较好。在训练神经网络模型时，我们可以事先将特征去相关并使得它们满足一个比较好的分布，这样，模型的第一层网络一般都会有一个比较好的输入特征，但是随着模型的层数加深，网络的非线性变换使得每一层的结果变得相关了，且不再满足 N(0, 1)

分布。更糟糕的是，可能这些隐藏层的特征分布已经发生了偏移。

论文的作者认为上面的问题会使得神经网络的训练变得困难，为了解决这个问题，他们提出在层与层之间加入Batch Normalization层。训练时，BN层利用隐藏层输出结果的均值 $\mu_\mathcal{B}$ 与方差 $\sigma^2_\mathcal{B}$ 来标准化每一层特征的分布，并且维护所有mini-batch数据的均值与方差，最后利用样本的均值与方差的无偏估计量用于测试时使用。

鉴于在某些情况下非标准化分布的层特征可能是最优的，标准化每一层的输出特征反而会使得网络的表达能力变得不好，作者为BN层加上了两个可学习的缩放参数 $\gamma$ 和偏移参数 $\beta$ 来允许模型自适应地去调整层特征分布。

BN层的作用

贴出论文中的两张图，就可以说明BN层的作用

使得模型训练收敛的速度更快
模型隐藏输出特征的分布更稳定，更利于模型的学习

BN的推导过程

1. 前向算法

Batch Normalization层的实现很简单，主要的过程由如下算法给出

首先计算出mini-batch的均值 $\mu_\mathcal{B}$ 与方差 $\sigma^2_\mathcal{B}$ ，接着对mini-batch中的每个特征 x_i

做标准化处理 $\hat{x_i}=\frac{x_i-\mu_\mathcal{B}}{\sqrt{\sigma^2_\mathcal{B}+\epsilon}}$ ，最后利用缩放参数 $\gamma$ 与偏移参数 $\beta$ 对特征 $\hat{x_i}$ 进行后处理得到输出。

当模型进行训练的时候，论文中提出记录每一个mini-batch的均值 $\mu_\mathcal{B}$ 与方差 $\sigma^2_\mathcal{B}$ ，在预测时利用均值 $\mu_\mathcal{B}$ 与方差 $\sigma^2_\mathcal{B}$ 的无偏估计量来进行BN操作，也就是

$\begin{align}&E(x)=E_\mathcal{B}(\mu_\mathcal{B})\\&Var(x)=\frac{m}{m-1}E_\mathcal{B}(\sigma^2_\mathcal{B})\end{align}$

输出也就表示为

$y=\frac{\gamma x}{\sqrt{Var(x)+\epsilon}}+(\beta-\frac{\gamma E(x)}{\sqrt{Var(x)+\epsilon}})$

2. 反向传播

BN层的反向传播相比于普通层要略微复杂一些，首先给出论文中的公式，对其中省略的步骤在下面会给出细致的推导过程。

对于上图中的式（2）（公式序号按图中次序），由下面的分解式给出

$\begin{align}&\frac{\partial l}{\partial \sigma^2_\mathcal{B}}=\frac{\partial l}{\partial \hat{X}}\frac{\partial \hat{X}}{\partial \sigma^2_\mathcal{B}}=\sum_{i=1}^{m}\frac{\partial l}{\partial \hat{x_i}}\frac{\partial \hat{x_i}}{\partial \sigma^2_\mathcal{B}}\\&\frac{\partial \hat{x_i}}{\partial \sigma^2_\mathcal{B}}=(x_i-\mu_\mathcal{B})\frac{-1}{2}(\sigma_\mathcal{B}^2+\epsilon)^{\frac{-3}{2}}\end{align}$

对于式（3），有

$\begin{align}&\frac{\partial l}{\partial \mu_\mathcal{B}}=\frac{\partial l}{\partial \hat{X}}\frac{\partial \hat{X}}{\partial \mu_\mathcal{B}}+\frac{\partial l}{\partial \sigma^2_\mathcal{B}}\frac{\partial \sigma^2_\mathcal{B}}{\partial \mu_\mathcal{B}}=\sum_{i=1}^{m}\frac{\partial l}{\partial \hat{x_i}}\frac{\partial \hat{x_i}}{\partial \mu_\mathcal{B}}+\frac{\partial l}{\partial \sigma^2_\mathcal{B}}\frac{\partial \sigma^2_\mathcal{B}}{\partial \mu_\mathcal{B}}\\&\frac{\partial \hat{x_i}}{\partial \mu_\mathcal{B}}=\frac{-1}{\sqrt{\sigma^2_\mathcal{B}+\epsilon}}\\&\frac{\partial \sigma^2_\mathcal{B}}{\partial \mu_\mathcal{B}}=\sum_{i=1}^{m}{\frac{-2(x_i-\mu_\mathcal{B})}{m}}\end{align}$

对于式（4），有

$\begin{align}&\frac{\partial l}{\partial x_i}=\frac{\partial l}{\partial \hat{x_i}}\frac{\partial \hat{x_i}}{\partial x_i}+\frac{\partial l}{\partial \sigma^2_\mathcal{B}}\frac{\partial \sigma^2_\mathcal{B}}{\partial x_i}+\frac{\partial l}{\partial \mu_\mathcal{B}}\frac{\partial \mu_\mathcal{B}}{\partial x_i}\\&\frac{\partial \hat{x_i}}{\partial x_i}=\frac{1}{\sqrt{\sigma^2_\mathcal{B}+\epsilon}}\\&\frac{\partial \sigma^2_\mathcal{B}}{\partial x_i}=\frac{2}{m}(x_i-\mu_\mathcal{B})(1-\frac{1}{m})+\frac{2}{m}\sum_{k=1, k \neq i}^{m}(x_i-\mu_\mathcal{B})(-\frac{1}{m})\\&=\frac{2}{m}(x_i-\mu_\mathcal{B})+\frac{2}{m}\sum_{k=1}^{m}(x_i-\mu_\mathcal{B})(-\frac{1}{m})\\&=\frac{2(x_i-\mu_\mathcal{B})}{m}\\&\frac{\partial \mu_\mathcal{B}}{\partial x_i}=\frac{1}{m}\end{align}$

若仔细观察式（3）与式（4），我们令

$\begin{align}&I_i=\frac{\partial l}{\partial \hat{x_i}}\frac{1}{\sqrt{\sigma^2_\mathcal{B}+\epsilon}}+\frac{\partial l}{\partial \sigma^2_\mathcal{B}}\frac{2(x_i-\mu_\mathcal{B})}{m}\\\end{align}$

则可以将式（3）与式（4）简化为

$\begin{align}&\frac{\partial l}{\partial \mu_\mathcal{B}}=-\sum_{i=1}^{m}I_i\\&\frac{\partial l}{\partial x_i}=I_i-\frac{1}{m}\sum_{i=1}^{m}I_i\end{align}$

这样做一个简单的替换，在实现代码的时候，运算会简化很多。式（1）（5）（6）的证明都很显然，在此略过了。

BN的代码实现

下面给出BN层的前向算法和反向传播的Python实现。

前面说过，论文中采用的是维护所有mini-batch的均值 $\mu_\mathcal{B}$ 与方差 $\sigma^2_\mathcal{B}$ ，最后利用无偏估计量进行预测。在这里我们实现另一种方案，利用一个动量参数 $\beta$ 维护一个动态均值 $r\mu_\mathcal{B}$ 与动态方差 $r\sigma^2_\mathcal{B}$ ，这样更方便简洁，torch7采用的也是这种方法，具体公式如下

$\begin{align}&r\mu_{\mathcal{B}i}=\beta r\mu_{\mathcal{B}i-1}+(1-\beta)\mu_\mathcal{B}\\&r\sigma^2_{\mathcal{B}i}=\beta r\sigma^2_{\mathcal{B}i-1}+(1-\beta)\sigma^2_\mathcal{B}\end{align}$

写代码的时候可以利用之前的文章中提到的快速计算方法，可以很方便的写出BN层前向算法和反向传播。

1. 前向算法

def batchnorm_forward(x, gamma, beta, bn_param):
    """
    Forward pass for batch normalization.

    Input:
    - x: Data of shape (N, D)
    - gamma: Scale parameter of shape (D,)
    - beta: Shift paremeter of shape (D,)
    - bn_param: Dictionary with the following keys:
    - mode: 'train' or 'test'; required
    - eps: Constant for numeric stability
    - momentum: Constant for running mean / variance.
    - running_mean: Array of shape (D,) giving running mean of features
    - running_var Array of shape (D,) giving running variance of features

    Returns a tuple of:
    - out: of shape (N, D)
    - cache: A tuple of values needed in the backward pass
    """
    mode = bn_param['mode']
    eps = bn_param.get('eps', 1e-5)
    momentum = bn_param.get('momentum', 0.9)

    N, D = x.shape
    running_mean = bn_param.get('running_mean', np.zeros(D, dtype=x.dtype))
    running_var = bn_param.get('running_var', np.zeros(D, dtype=x.dtype))

    out, cache = None, None
    
    if mode == 'train':

        sample_mean = np.mean(x, axis=0)
        sample_var = np.var(x, axis=0)
        out_ = (x - sample_mean) / np.sqrt(sample_var + eps)

        running_mean = momentum * running_mean + (1 - momentum) * sample_mean
        running_var = momentum * running_var + (1 - momentum) * sample_var

        out = gamma * out_ + beta
        cache = (out_, x, sample_var, sample_mean, eps, gamma, beta)

    elif mode == 'test':

        scale = gamma / np.sqrt(running_var + eps)
        out = x * scale + (beta - running_mean * scale)

    else:
        raise ValueError('Invalid forward batchnorm mode "%s"' % mode)

    # Store the updated running means back into bn_param
    bn_param['running_mean'] = running_mean
    bn_param['running_var'] = running_var

    return out, cache

2. 反向传播

def batchnorm_backward(dout, cache):
    """
    Backward pass for batch normalization.

    Inputs:
    - dout: Upstream derivatives, of shape (N, D)
    - cache: Variable of intermediates from batchnorm_forward.

    Returns a tuple of:
    - dx: Gradient with respect to inputs x, of shape (N, D)
    - dgamma: Gradient with respect to scale parameter gamma, of shape (D,)
    - dbeta: Gradient with respect to shift parameter beta, of shape (D,)
    """
    dx, dgamma, dbeta = None, None, None

    out_, x, sample_var, sample_mean, eps, gamma, beta = cache

    N = x.shape[0]
    dout_ = gamma * dout
    dvar = np.sum(dout_ * (x - sample_mean) * -0.5 * (sample_var + eps) ** -1.5, axis=0)
    dx_ = 1 / np.sqrt(sample_var + eps)
    dvar_ = 2 * (x - sample_mean) / N

    # intermediate for convenient calculation
    di = dout_ * dx_ + dvar * dvar_
    dmean = -1 * np.sum(di, axis=0)
    dmean_ = np.ones_like(x) / N

    dx = di + dmean * dmean_
    dgamma = np.sum(dout * out_, axis=0)
    dbeta = np.sum(dout, axis=0)

    return dx, dgamma, dbeta