数据结构：散列（hashing）

声明：本文为学习数据结构与算法分析(第三版) Clifford A.Shaffer 著的学习笔记，代码有参考该书的示例代码。

散列方法

把关键码值映射到数组中的位置来访问记录这个过程称为散列（hashing）
把关键码值映射到位置的函数称为散列函数（hashing function），通常用 h 表示。
存放记录的数组称为散列表（hash table），用 HT 表示。
散列表中的一个位置称为一个槽（slot）。
散列表 HT 中的数目用变量 M 表示，槽从 0 到 M-1标号。
散列方法通常不适用于允许多条记录有相同关键码值的应用程序。散列方法一般不适用于范围检索。
对于一个散列函数 h 和两个关键码值k₁ 、 k₂，如果 h(k₁) =B= h(k₂) ，其中 B 为表中的一个槽，那么就说 k₁ 和 k₂ 对于 B 在散列函数 h 下有冲突。
对于冲突，有开散列和闭散列的解决方式。

散列函数

从技术上来说，任何能把所有可能关键码值映射到散列表槽中的函数都是散列函数。
下面介绍一个常用的散列函数

平方取中方法

平方取中方法是一个用于数值的散列方法。对关键码计算平方，取中间的几位，散列到相应的位置。
这样计算的原因是因为关键码的大多数位或所有位对结果都有贡献。
比如，基数为 10 的四位关键码，散列到一个长度为 100 的散列表中。假如关键码为 4567 ，则

4567 * 4567 = 20857489

取的中间两位是 57 。（位数等于 ln100 ）

折叠方法

这是一个用于字符串的散列方法，计算的方法是将字符串的 ASCII 值累加起来，对 M 求模。

int h(char* str)
{
    int sum, i;
    for(sum = i = 0; str[i] != '\0'; ++i)
        sum += static_cast<int>(str[i]);
    return sum % M;
}

这个方法有一个不好的地方就是，假如 sum 的值比 M 小，则会产生比较差的分布。

将字符串解释为无符号整型和的散列方法

由于找不到这个方法的名字，就这么叫吧。
这种散列方法的计算方式是，将字符串解释为一个个大小为 4 的无符号整型，求和，然后求模。

int sfold(char* str)
{
    unsigned int sum = 0;
    unsigned int* intKey = static_cast<decltype(intKey)>(str);
    int len = strlen(str)/4;
    for(int i =0;i<len;++i)
        sum += intKey[i];

    int extra = strlen(str)-len*4;
    char temp[4];
    intKey = static_cast<decltype(intKey)>(temp);//or reinterpret_cast?
    intKey[0] = 0;
    for(int i =0;i<extra;++i)
        temp[i] = str[len*4+i];
    sum += intKey[0];
    return sum%M;
}

使用无符号整数的目的是为了避免求模时结果会是负数。
在就算的过程中，如果数字过大，则会发生溢出。但是作为散列函数，并没有关系。（意思就是，让它溢出吧）

开散列方法

尽管散列函数的目的是尽量减少冲突，但是有些冲突是不可避免的。
解决冲突的技术可以分为两类：开散列方法（open hashing，也称单链方法，separate chaining）和闭散列方法（closed hashing，也称开地址方法，open addressing）
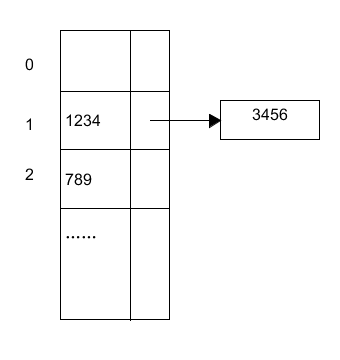
开散列方法解决冲突是将冲突记录在表外，而闭散列方法是将冲突记录在表内的另一个空槽。

看起来就好像很好实现的样子，于是我就是实现了一下。
在我的实现中 M 为11，散列函数如下：

    int h(const Key& k) const
    {
        return k*7%M;
    }

实话说，这并不是一个好的散列函数。

闭散列方法

闭散列方法将所有记录都直接存储在散列表中。
闭散列方法有集中散列方式：桶式散列、线性探查、二次探查、双散列方法。

桶式散列

桶式散列是把散列的槽分成多个桶（bucket）。
把散列表中的 M 个槽分成 B 个桶，每个桶中包含 M/B 个槽。
散列函数把每一条记录分配到某个桶的第一个槽中。如果这个槽已经被占用，那么就顺序地沿着桶查找，直到找到一个空槽。
如果没有空槽了，那么就将该条记录分配到一个具有无限容量的溢出桶中。

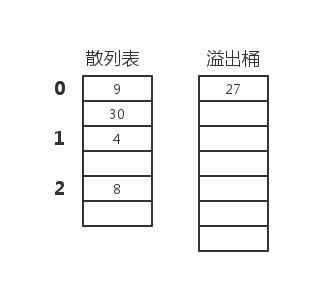
插入顺序是

9 30 27 4 8

有6个槽，3个桶的散列表，散列函数是

int h(int i)
{
    return i%B;
}

我想这样应该表达明确了吧。
桶式散列的一个简单变体是，先把关键码散列到槽中。当该槽满时，再把关键码散列到同一个桶的其他槽中。如果还没有空槽，就散列到溢出桶中。

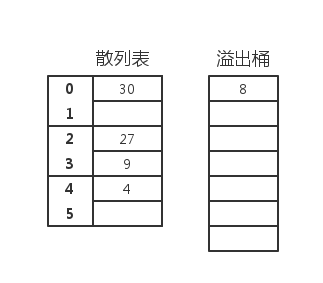
这时散列函数是：

int h(int i)
{
    return i%M;
}

线性探查

线性探查是比较常用的散列函数，它不使用桶式散列的方法，而是允许记录存储在散列表中的任何一个空槽中。
冲突解决策略是产生一组有可能放置该记录的槽，第一个槽就是该关键码的基槽。如果基槽被占用了，那么就会寻找下一个槽，直到记录被存放。
这组槽就称为冲突解决策略产生的探查序列（probe sequence）。
探查序列是由探查函数（probe function）的 p 函数生成的。
注意，探查函数返回的是相对于初始位置的偏移量，而不是散列表的一个槽。
线性探查的函数类似如下：

int p(int k, int i)
{
    return a*i+b;
}

其中 i 是第几次的探查参数， k 是关键码，a 和 b 是常数。
使用的时候如下：

return (h(k)+p(k, i))%M;

为了是探查列走遍所有的槽，a 必须与 M互素。

线性探查会导致：基本聚集（primary clustering）
考虑顺序插入：

9 30 27 4 8

加入使用最基本的探查函数 return i; M为6
那么 9 的探查序列：

3 4 5 0 1 2

而 27 的探查序列也是如此。
到插入的记录多了，就是大部分地聚集到一起。
把记录聚集到一起的倾向就是基本聚集了。
好的探查函数应该是使得它们的探查序列岔开。
而解决基本聚集问题就是使用二次探查或伪随机探查。

二次探查

二次探查的函数如下：

int p(int k, int i)
{
    return a*i*i+b*i+c;
}

其中 a， b， c 为常数。
二次探查的缺陷在于，在某些特定的情况下，只有特定的槽被探查到。
考虑 M 为 3，p(k, i) = i*i;
那么散列到槽 0 的只会探查到 0， 1 ，而不会探查到 2。
然而，这样的情况是可以在低开销的基础上探查得到较好的结果。

当散列表长度为素数，以及探查函数为 p(k, i) = i*i 时，至少能够访问到表中一半的槽。
如果散列表长为 2 的指数，并且探查函数为 p(k, i) = (i*i+i)/2 ， 那么表中所有槽都能被探查序列访问到。

伪随机探查

在伪随机探查中，探查序列中的第 i 个槽是 (h(k) + ri) mod M ，ri是 1 到 M-1 之间的数的随机序列。
所有的插入和检索都使用相同的伪随机序列。

尽管二次探查和伪随机探查能够解决基本聚集问题，然而如果散列函数在某个基槽聚集，依然会保持聚集。这个问题称为二次聚集（secondary clustering）
解决二次聚集问题可以使用双散列方法

双散列方法

双散列方法的形式：

int p(int k, int i)
{
    return i*h2(k);
}

h2 是第二个散列函数
好的双散列实现方法应当保证所有探查序列常数都与表 M 长度互素。
其中一种方法是设置 M 为素数，而h2 返回 1<=h2<=M-1 之间的值。
另外一种方法是给定一个 m 值，设置 M = 2^m ，然后让 h2 返回 1 到 2^m 之间的一个奇数值。

闭散列方法结论

每个新插入操作产生的额外查找代价将在散列表接近半满时急剧增加。
如果还考虑到访问模式，在理想情况下，记录应当沿着探查序列按照访问频率排序。

删除

删除记录的时候，要考虑到两点：

1. 删除不应当影响后面的检索。
2. 删除的槽应当可以为后来的插入操作所使用。

通过在删除的槽中放置一个特殊的标记就可以解决这个问题。这个标记称为墓碑（tombstone）。

如果不想使用墓碑的标记，还可以在删除的时候进行一次局部的重组，或者定期重组散列表。

本文实现了开散列方法和闭散列方法中的一种。
代码在本人的 github 上可以找到。
我的github
–END–