“Xavier”初始化方法是一种很有效的神经网络初始化方法,方法来源于2010年的一篇论文《Understanding the difficulty of training deep feedforward neural networks》,可惜直到近两年,这个方法才逐渐得到更多人的应用和认可。
为了使得网络中信息更好的流动,每一层输出的方差应该尽量相等。
基于这个目标,现在我们就去推导一下:每一层的权重应该满足哪种条件。
文章先假设的是线性激活函数,而且满足0点处导数为1,即
现在我们先来分析一层卷积:
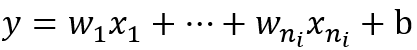
其中ni表示输入个数。
根据概率统计知识我们有下面的方差公式:
特别的,当我们假设输入和权重都是0均值时(目前有了BN之后,这一点也较容易满足),上式可以简化为:
进一步假设输入x和权重w独立同分布,则有:
于是,为了保证输入与输出方差一致,则应该有:
对于一个多层的网络,某一层的方差可以用累积的形式表达:
特别的,反向传播计算梯度时同样具有类似的形式:
综上,为了保证前向传播和反向传播时每一层的方差一致,应满足:
但是,实际当中输入与输出的个数往往不相等,于是为了均衡考量,最终我们的权重方差应满足:
———————————————————————————————————————
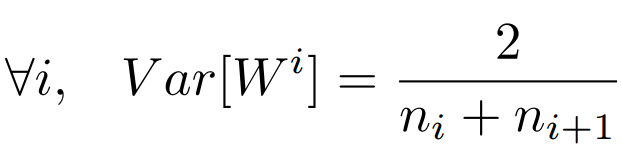
———————————————————————————————————————
学过概率统计的都知道 [a,b] 间的均匀分布的方差为:
因此,Xavier初始化的实现就是下面的均匀分布:
——————————————————————————————————————————
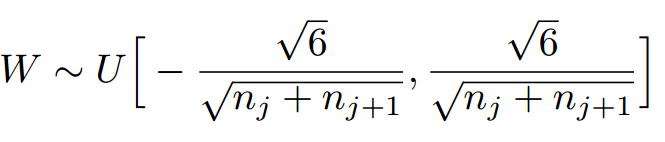
———————————————————————————————————————————
下面,我们来看一下caffe中具体是怎样实现的,代码位于include/caffe/filler.hpp文件中。
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
由上面可以看出,caffe的Xavier实现有三种选择
(1) 默认情况,方差只考虑输入个数:
(2) FillerParameter_VarianceNorm_FAN_OUT,方差只考虑输出个数:
(3) FillerParameter_VarianceNorm_AVERAGE,方差同时考虑输入和输出个数:
之所以默认只考虑输入,我个人觉得是因为前向信息的传播更重要一些
作者:冯超
链接:https://zhuanlan.zhihu.com/p/22028079
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
上一回我们做了三个小实验。第一个是正常的实验,表现优异;第二个实验我们把初始化调整得很奇葩(为什么奇葩?),最终训练结果弱爆了;第三个实验我们把非线性函数重新换回sigmoid,模型奇迹般地回血,虽然表现不够完美,但也算是十分优异了。
于是ReLU被众人推到墙角,开始质问。
其实ReLU也是很委屈的,前面说过他的优势在与模型前向后向计算的过程中,它可以更好地传递数据,不会像sigmoid那样有梯度传递的问题,但是它又缺少了sigmoid的重要特性,那就是对数据的控制力。
我们知道sigmoid可以把任意维度的数据压缩到0到1之间,这是它最强力的一个特点。所以在使用sigmoid时,我们不用太担心数据的幅度问题,因为只要使用一个sigmoid,数据的幅度就会得到良好的控制(当然了,全是正数这件事其实也有点不太靠谱,要是像tanh那样有正有负就更好了)。而我们从上一次的实验中可以看出,采用ReLU的非线性函数,数据的维度完全没有得到控制。有的幅度到达了上千,有的依然是一个极小的小数。这说明ReLU在压缩数据幅度方面存在劣势。
于是乎我们有了以下的经验总结:
- sigmoid在压缩数据幅度方面有优势,对于深度网络,使用sigmoid可以保证数据幅度不会有问题,这样数据幅度稳住了就不会出现太大的失误。
- 但是sigmoid存在梯度消失的问题,在反向传播上有劣势,所以在优化的过程中存在不足
- relu不会对数据做幅度压缩,所以如果数据的幅度不断扩张,那么模型的层数越深,幅度的扩张也会越厉害,最终会影响模型的表现。
- 但是relu在反向传导方面可以很好地将“原汁原味”的梯度传到后面,这样在学习的过程中可以更好地发挥出来。(这个“原汁原味”只可意会,不必深究)
这么来看,sigmoid前向更靠谱,relu后向更强。这么一看似乎一切又回到了起点,到底哪个非线性函数更好呢?
要评判哪个非线性函数更好,不但要看自己本身,还要看它们和整体模型阵型的搭配情况(BP很重要!)sigmoid在学习方面存在弱点,有什么办法能帮助它呢?这个我们后面再说。那relu的数据幅度呢?有没有什么办法能够帮助它解决呢?
众人想了好久,又重新看向了初始化……
初始化:(黑人问号脸)?
xavier
大家突然想起来,刚才和relu完美配合的那个初始化叫什么来着?哦对,xavier。我们就来看看这个初始化方法的由来。xavier诞生时并没有用relu做例子,但是实际效果中xavier还是和relu很搭配的。
xavier是如何完成初始化工作的呢?它的初始化公式如下所示:
定义参数所在层的输入维度为n,输出维度为m,那么参数将以均匀分布的方式在![[-\sqrt{\frac{6}{m+n}},\sqrt{\frac{6}{m+n}}]](https://i-blog.csdnimg.cn/blog_migrate/926c96daf581dc66fe5e7a8a165de48f.png) 的范围内进行初始化。
的范围内进行初始化。
那么这个公式是如何计算出来的呢?关于这个问题我们需要一段漫长的推导。在推导之前我们要强调一个关键点,就是参数的标准差,或者方差。前面我们提到了Caffe中的debug_info主要展示了数据的L1 norm,对于均值为0的数据来说,这个L1 norm可以近似表示标准差。
我们将用到以下和方差相关的定理:
假设有随机变量x和w,它们都服从均值为0,方差为 的分布,那么:
的分布,那么:
- w*x就会服从均值为0,方差为
 的分布
的分布
- w*x+w*x就会服从均值为0,方差为
 的分布
的分布
以下内容主要来自论文《Understanding the difficulty of training deep feedforward neural network》的理解,这里将以我个人的理解做一下解读,如果有错欢迎来喷。
前面两个定理的变量名称是不是有点熟悉?没错,下面我们说的就是参数w和x。这里暂时将偏置项放在一边,同时我们还要把一个部分放在一边,那就是非线性部分。这篇论文心目中的理想非线性函数是tanh。为啥呢?
在大神的假想世界中,x和w都是靠近0的比较小的数字,那么它们最终计算出来的数字也应该是一个靠近0,比较小的数字。我们再看一眼tanh函数和它对应的梯度函数:

 这两张图有点大,不过可以看出来,如果数值集中在0附近,我们可以发现,前向时tanh靠近0的地方斜率接近1,所以前辈告诉我们,把它想象成一个线性函数。
这两张图有点大,不过可以看出来,如果数值集中在0附近,我们可以发现,前向时tanh靠近0的地方斜率接近1,所以前辈告诉我们,把它想象成一个线性函数。
下面这张梯度的图像也是一样,靠近0的地方斜率接近1,所以前辈又一次告诉我们,把它想象成一个线性函数。
什么,你不信?
把它想象成一个线性函数。
把它想象成一个线性函数。
把它想象成一个线性函数……
好了,现在这个挡在中间的非线性函数硬生生掰成一个线性函数了,为了理论的完美我们也是什么也不顾了。下面就要面对一个问题,如何让深层网络在学习过程中的表现像浅层网络?
我们的脑中迅速回忆起我们接触过的浅层模型——logistic regression,SVM。为了它们的表现能够更好,我们都会把特征做初始化,细心处理,比方说做白化处理,使他的均值方差保持好,然后用浅层模型一波训练完成。现在我们采用了深层模型,输入的第一层我们是可以做到数据的白化的——减去均值,除以一个标准差。但是里面层次的数据,你总不好伸手进入把它们也搞白化吧!(当然,后来真的有人伸进去了,还做得不错)那我们看看如果在中间层不做处理会发生什么?
我们假设所有的输入数据x满足均值为0,方差为的分布,我们再将参数w以均值为0,方差为
的方式进行初始化。我们假设第一次是大家喜闻乐见的卷积层,卷积层共有n个参数(n=channel*kernel_h*kernel_w),于是为了计算出一个线性部分的结果,我们有:

这个公式的下标不准确,大家姑且这么看了,也就是说,线性输出部分的一个结果值,实际上是由n个乘加计算出来的,那么下面是一道抢答题,按照我们刚才对x和w的定义,加上前面我们说过的两个方差计算公式,这个z会服从一个什么分布呢?
均值肯定还是0嘛,没得说。
方差好像积累了一大堆东西:
然后我们通过那个靠意念构建的具有“线性特征”的非线性层,奇迹般地发现一切都没有变化,那么下一层的数据就成了均值为0,方差为 的“随机变量”(姑且称之为随机变量吧)。
的“随机变量”(姑且称之为随机变量吧)。
为了更好地表达,我们将层号写在变量的上标处,于是就有:

我们将卷积层和全连接层统一考虑成n个参数的一层,于是接着就有:

如果我们是一个k层的网络(这里主要值卷积层+全连接层的总和数),我们就有

继续把这个公式展开,就会得到它的最终形态:

可以看出,后面的那个连乘实际上看着就像个定时炸弹(相信看到这,我应该能成功地吸引大家的注意力,帮助大家把非线性函数线性化的事情忘掉了……),如果 总是大于1,那么随着层数越深,数值的方差会越来越大,反过来如果乘积小于1,那么随着层数越深,数值的方差就会越来越小。
总是大于1,那么随着层数越深,数值的方差会越来越大,反过来如果乘积小于1,那么随着层数越深,数值的方差就会越来越小。
越来越大,就容易Hold不住导致溢出,越来越小,就容易导致数据差异小而不易产生有力的梯度。这就是深层模型的一大命门。
公式推到这里,我们不妨回头看看这个公式:

你一定会有这样一个想法(一定会有!),如果,接着我们保证每一层输入的方差都保持一致,那么数值的幅度不就可以解决了么?于是乎:

我们用均值为1,方差为上式的那个数字做初始化,不就可以解决了?
不错,从理论上讲是这个思路,不过,这只是这个思路的开始……
本次简单介绍一下MSRA初始化方法,方法同样来自于何凯明paper 《Delving Deep into Rectifiers:Surpassing Human-Level Performance on ImageNet Classification》.
Motivation
网络初始化是一件很重要的事情。但是,传统的固定方差的高斯分布初始化,在网络变深的时候使得模型很难收敛。此外,VGG团队是这样处理初始化的问题的:他们首先训练了一个8层的网络,然后用这个网络再去初始化更深的网络。
“Xavier”是一种相对不错的初始化方法,我在我的另一篇博文“深度学习——Xavier初始化方法”中有介绍。但是,Xavier推导的时候假设激活函数是线性的,显然我们目前常用的ReLU和PReLU并不满足这一条件。
MSRA初始化
只考虑输入个数时,MSRA初始化是一个均值为0方差为2/n的高斯分布:
推导证明
推导过程与Xavier类似。
首先,用下式表示第L层卷积:
则其方差为:(假设x和w独立,且各自的每一个元素都同分布,即下式中的n_l表示输入元素个数,x_l和w_l都表示单个元素)
当权重W满足0均值时,上述方差可以进一步写为:
对于ReLU激活函数,我们有:(其中f是激活函数)
带入之前的方差公式则有:
由上式易知,为了使每一层数据的方差保持一致,则权重应满足:
补充说明
(1) 对于第一层数据,由于其之前没有经过ReLU,因此理论上这一层的初始化方差应为1/n。但是,因为只有一层,系数差一点影响不大,因此为了简化操作整体都采用2/n的方差;
(2) 反向传播需要考虑的情况完全类似于“Xavier”。对于反向传播,可以同样进行上面的推导,最后的结论依然是方差应为2/n,只不过因为是反向,这里的n不再是输入个数,而是输出个数。文章中说,这两种方法都可以帮助模型收敛。
(3) 对于PReLU激活函数来说,条件变成了:
因此初始化和PReLU有关,但是目前caffe的代码并不在支持在MSRA初始化时手动指定a的值。
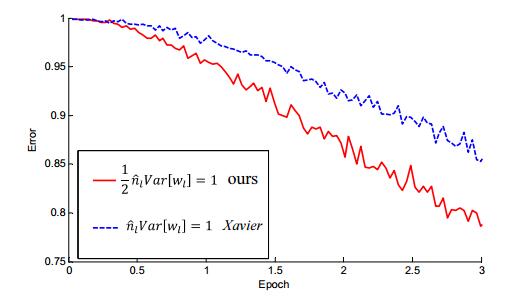
(4) 文章做了一些对比试验,表明在网络加深后,MSRA初始化明显优于Xavier初始化。
特别当网络增加到33层之后,对比效果更加明显
caffe中权值初始化方法
首先说明:在caffe/include/caffe中的 filer.hpp文件中有它的源文件,如果想看,可以看看哦,反正我是不想看,代码细节吧,现在不想知道太多,有个宏观的idea就可以啦,如果想看代码的具体的话,可以看:http://blog.csdn.net/xizero00/article/details/50921692,写的还是很不错的(不过有的地方的备注不对,不知道改过来了没)。
文件 filler.hpp提供了7种权值初始化的方法,分别为:常量初始化(constant)、高斯分布初始化(gaussian)、positive_unitball初始化、均匀分布初始化(uniform)、xavier初始化、msra初始化、双线性初始化(bilinear)。
275 Filler<Dtype>* GetFiller(const FillerParameter& param) { 276 const std::string& type = param.type(); 277 if (type == "constant") { 278 return new ConstantFiller<Dtype>(param); 279 } else if (type == "gaussian") { 280 return new GaussianFiller<Dtype>(param); 281 } else if (type == "positive_unitball") { 282 return new PositiveUnitballFiller<Dtype>(param); 283 } else if (type == "uniform") { 284 return new UniformFiller<Dtype>(param); 285 } else if (type == "xavier") { 286 return new XavierFiller<Dtype>(param); 287 } else if (type == "msra") { 288 return new MSRAFiller<Dtype>(param); 289 } else if (type == "bilinear") { 290 return new BilinearFiller<Dtype>(param); 291 } else { 292 CHECK(false) << "Unknown filler name: " << param.type(); 293 } 294 return (Filler<Dtype>*)(NULL); 295 }
并且结合 .prototxt 文件中的 FillerParameter来看看怎么用:
43 message FillerParameter { 44 // The filler type. 45 optional string type = 1 [default = 'constant']; 46 optional float value = 2 [default = 0]; // the value in constant filler 47 optional float min = 3 [default = 0]; // the min value in uniform filler 48 optional float max = 4 [default = 1]; // the max value in uniform filler 49 optional float mean = 5 [default = 0]; // the mean value in Gaussian filler 50 optional float std = 6 [default = 1]; // the std value in Gaussian filler 51 // The expected number of non-zero output weights for a given input in 52 // Gaussian filler -- the default -1 means don't perform sparsification. 53 optional int32 sparse = 7 [default = -1]; 54 // Normalize the filler variance by fan_in, fan_out, or their average. 55 // Applies to 'xavier' and 'msra' fillers. 56 enum VarianceNorm { 57 FAN_IN = 0; 58 FAN_OUT = 1; 59 AVERAGE = 2; 60 } 61 optional VarianceNorm variance_norm = 8 [default = FAN_IN]; 62 }
constant初始化方法:
它就是把权值或着偏置初始化为一个常数,具体是什么常数,自己可以定义啦。它的值等于上面的.prototxt文件中的 value 的值,默认为0
下面是是与之相关的.proto文件里的定义,在定义网络时,可能分用到这些参数。
45 optional string type = 1 [default = 'constant']; 46 optional float value = 2 [default = 0]; // the value in constant filler
uniform初始化方法
它的作用就是把权值与偏置进行 均匀分布的初始化。用min 与 max 来控制它们的的上下限,默认为(0,1).
下面是是与之相关的.proto文件里的定义,在定义网络时,可能分用到这些参数。
45 optional string type = 1 [default = 'constant']; 47 optional float min = 3 [default = 0]; // the min value in uniform filler 48 optional float max = 4 [default = 1]; // the max value in uniform filler
Gaussian 初始化
给定高斯函数的均值与标准差,然后呢?生成高斯分布就可以了。
不过要说明一点的就是, gaussina初始化可以进行 sparse,意思就是可以把一些权值设为0. 控制它的用参数 sparse. sparse表示相对于 num_output来说非0的个数,在代码实现中,会把 sparse/num_output 作为 bernoulli分布的概率,明白?? 生成的bernoulli分布的数字(为0或1)与原来的权值相乖,就可以实现一部分权值为0了。即然这样,我有一点不明白,为什么不直接把sparsr定义成概率呢??这样多么简单啦,并且好明白啊。。对于 num_output是什么,你在定义你的网络的.prototxt里,一定分有的啦,不信你去看看;
下面是是与之相关的.proto文件里的定义,在定义网络时,可能分用到这些参数。
45 optional string type = 1 [default = 'constant']; 49 optional float mean = 5 [default = 0]; // the mean value in Gaussian filler 50 optional float std = 6 [default = 1]; // the std value in Gaussian filler 51 // The expected number of non-zero output weights for a given input in 52 // Gaussian filler -- the default -1 means don't perform sparsification. 53 optional int32 sparse = 7 [default = -1];
positive_unitball 初始化
通俗一点,它干了点什么呢?即让每一个单元的输入的权值的和为 1. 例如吧,一个神经元有100个输入,这样的话,让这100个输入的权值的和为1. 源码中怎么实现的呢? 首先给这100个权值赋值为在(0,1)之间的均匀分布,然后,每一个权值再除以它们的和就可以啦。
感觉这么做,可以有助于防止权值初始化过大,使激活函数(sigmoid函数)进入饱和区。所以呢,它应该比适合simgmoid形的激活函数。
它不需要参数去 控制。
XavierFiller初始化:
对于这个初始化的方法,是有理论的。它来自这篇论文《Understanding the difficulty of training deep feedforward neural networks》。在推导过程中,我们认为处于 tanh激活函数的线性区,所以呢,对于ReLU激活函数来说,XavierFiller初始化也是很适合啦。
如果不想看论文的话,可以看看 https://zhuanlan.zhihu.com/p/22028079,我觉得写的很棒,另外,http://blog.csdn.net/shuzfan/article/details/51338178可以作为补充。
它的思想就是让一个神经元的输入权重的(当反向传播时,就变为输出了)的方差等于:1 / 输入的个数;这样做的目的就是可以让信息可以在网络中均匀的分布一下。
对于权值的分布:是一个让均值为0,方差为1 / 输入的个数 的 均匀分布。
如果我们更注重前向传播的话,我们可以选择 fan_in,即正向传播的输入个数;如果更注重后向传播的话,我们选择 fan_out, 因为吧,等着反向传播的时候,fan_out就是神经元的输入个数;如果两者都考虑的话,那就选 average = (fan_in + fan_out) /2
下面是是与之相关的.proto文件里的定义,在定义网络时,可能分用到这些参数。
45 optional string type = 1 [default = 'constant']; 54 // Normalize the filler variance by fan_in, fan_out, or their average. 55 // Applies to 'xavier' and 'msra' fillers. 56 enum VarianceNorm { 57 FAN_IN = 0; 58 FAN_OUT = 1; 59 AVERAGE = 2; 60 } 61 optional VarianceNorm variance_norm = 8 [default = FAN_IN];
MSRAFiller初始化方式
它与上面基本类似,它是基于《Delving Deep into Rectifiers:Surpassing Human-Level Performance on ImageNet Classification》来推导的,并且呢,它是基于激活函数为 ReLU函数哦,
对于权值的分布,是基于均值为0,方差为 2 /输入的个数 的高斯分布,这也是和上面的Xavier Filler不同的地方;它特别适合激活函数为 ReLU函数的啦。
下面是是与之相关的.proto文件里的定义,在定义网络时,可能分用到这些参数。
45 optional string type = 1 [default = 'constant']; 54 // Normalize the filler variance by fan_in, fan_out, or their average. 55 // Applies to 'xavier' and 'msra' fillers. 56 enum VarianceNorm { 57 FAN_IN = 0; 58 FAN_OUT = 1; 59 AVERAGE = 2; 60 } 61 optional VarianceNorm variance_norm = 8 [default = FAN_IN];
BilinearFiller初始化
对于它,要还没有怎么用到过,它常用在反卷积神经网络里的权值初始化;
直接上源码,大家看看吧;
213 /*! 214 @brief Fills a Blob with coefficients for bilinear interpolation. 215 216 A common use case is with the DeconvolutionLayer acting as upsampling. 217 You can upsample a feature map with shape of (B, C, H, W) by any integer factor 218 using the following proto. 219 \code 220 layer { 221 name: "upsample", type: "Deconvolution" 222 bottom: "{{bottom_name}}" top: "{{top_name}}" 223 convolution_param { 224 kernel_size: {{2 * factor - factor % 2}} stride: {{factor}} 225 num_output: {{C}} group: {{C}} 226 pad: {{ceil((factor - 1) / 2.)}} 227 weight_filler: { type: "bilinear" } bias_term: false 228 } 229 param { lr_mult: 0 decay_mult: 0 } 230 } 231 \endcode 232 Please use this by replacing `{{}}` with your values. By specifying 233 `num_output: {{C}} group: {{C}}`, it behaves as 234 channel-wise convolution. The filter shape of this deconvolution layer will be 235 (C, 1, K, K) where K is `kernel_size`, and this filler will set a (K, K) 236 interpolation kernel for every channel of the filter identically. The resulting 237 shape of the top feature map will be (B, C, factor * H, factor * W). 238 Note that the learning rate and the 239 weight decay are set to 0 in order to keep coefficient values of bilinear 240 interpolation unchanged during training. If you apply this to an image, this 241 operation is equivalent to the following call in Python with Scikit.Image. 242 \code{.py} 243 out = skimage.transform.rescale(img, factor, mode='constant', cval=0) 244 \endcode 245 */ 246 template <typename Dtype> 247 class BilinearFiller : public Filler<Dtype> { 248 public: 249 explicit BilinearFiller(const FillerParameter& param) 250 : Filler<Dtype>(param) {} 251 virtual void Fill(Blob<Dtype>* blob) { 252 CHECK_EQ(blob->num_axes(), 4) << "Blob must be 4 dim."; 253 CHECK_EQ(blob->width(), blob->height()) << "Filter must be square"; 254 Dtype* data = blob->mutable_cpu_data(); 255 int f = ceil(blob->width() / 2.); 256 float c = (2 * f - 1 - f % 2) / (2. * f); 257 for (int i = 0; i < blob->count(); ++i) { 258 float x = i % blob->width(); 259 float y = (i / blob->width()) % blob->height(); 260 data[i] = (1 - fabs(x / f - c)) * (1 - fabs(y / f - c)); 261 } 262 CHECK_EQ(this->filler_param_.sparse(), -1) 263 << "Sparsity not supported by this Filler."; 264 } 265 };








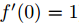
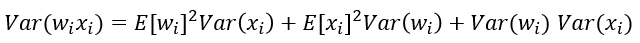
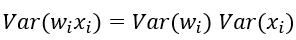
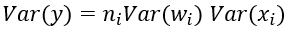
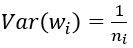
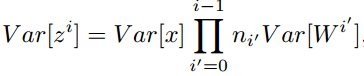
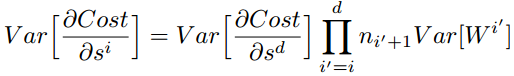
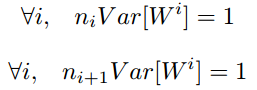
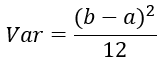
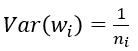
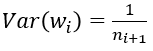
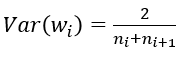
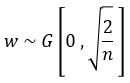
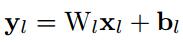
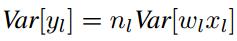
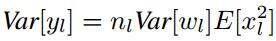
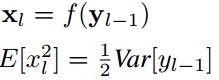
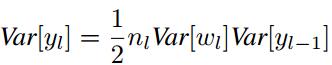
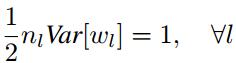
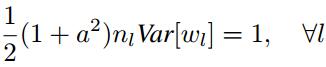















 1684
1684

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








