形态学滤波在心电图ECG中的应用

1.算法介绍

什么是形态学滤波？

形态学滤波的定义为一种分析空间结构的理论，目标是分析目标的形状和结构。具体理论就不展开讲，直接来看是怎么实现的，也就是数学模型定义是怎样的，定义如下：

图1 形态学滤波

从上图可以看出，形态学滤波里面两个核心的计算就是开运算和闭运算，那么开运算和闭运算又是怎么定义的呢？

开运算定义为先腐蚀后膨胀，闭运算定义为先膨胀后腐蚀，最终腐蚀和膨胀定义如下：

信号f定义为在F={0,1,2,3,4.....N-1}上的离散函数

结果元素K定义为在K={0,1,2,3,4...M-1}上的离散函数

腐蚀运算定义如下：其中 m的范围为0,1,2....,N-M.

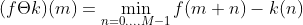
膨胀定义如下：其中m的范围为M-1....N-1

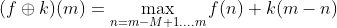
从定义的数学模型中，我们可以比较简单的实现形态学滤波算法。

2.在心电图ECG滤波中的应用

前面说了，形态学滤波能分析目标的形状和结构，这里我们假定我们的结构元素设定为直线型，从上面可以看出腐蚀运算，当前时刻的输出是未来M个元素找波谷（最小值），且到信号接近末端时，由于信号不够，无法运算，即尾部的M个元素是无效的。

同理可以看出膨胀运算，当前时刻的输出是过去M个元素找波峰（最大值），且在信号的前M个元素，由于信号不够，无法运算，即头部的M个元素是无效的。

而开运算是先腐蚀后膨胀，可以去除ECG信号的波峰，闭运算是先膨胀后腐蚀，可以去除ECG信号的波谷，而去除的波峰、波谷的宽度最大值又和结构元素的长度M相关，利用这个特性，我们可以设计一个宽度为M的直线型结构的形态学滤波，利用开运算和闭运算去除ECG信号的有效波（P波，QRS波,T波），剩下的无用信号即为基线漂移部分，这就是利用形态学滤波去除心电图ECG基线漂移。

接下来设计形态学滤波滤除基线漂移的算法：（假定ECG采样率为250Hz）

1.先去除ECG信号的比较窄的波，如重要的QRS波，结构元素为直线型，为了计算量小，结构元素的幅度可以直接设置为0，结构元素宽度为28，输入信号为原始信号x，进行形态学滤波，得到y1。

2.再去除ECG信号的比较框的波，如T波,同样的结构元素为直线型，为了计算量小，结构元素的幅度可以直接设置为0，结构元素宽度为70，输入信号为原始信号y1，进行形态学滤波，得到y2。

3.得到的的y2即为无用信号，也就是基线漂移部分，用原始信号x减去y2，即为最终想要的信号。

ps: 这里结构元素的长度可能需要根据实际情况和经验适当做调整。

3.试验

通过前面章节，实现算法后，拿实际产品进行尝试，发现形态学滤波，在滤除基线漂移上很擅长，实际效果如下：

图2 形态学滤波

但是形态学滤ECG基线漂移也有不足之处，如果漂移很严重，形态学滤波可以把漂移滤掉，但也同时会导致T波出现比较严重的失真。