Blocks
| Time Limit: 5000MS | Memory Limit: 65536K | |
| Total Submissions: 4269 | Accepted: 1716 |
Description
Some of you may have played a game called 'Blocks'. There are n blocks in a row, each box has a color. Here is an example: Gold, Silver, Silver, Silver, Silver, Bronze, Bronze, Bronze, Gold.
The corresponding picture will be as shown below:

Figure 1
If some adjacent boxes are all of the same color, and both the box to its left(if it exists) and its right(if it exists) are of some other color, we call it a 'box segment'. There are 4 box segments. That is: gold, silver, bronze, gold. There are 1, 4, 3, 1 box(es) in the segments respectively.
Every time, you can click a box, then the whole segment containing that box DISAPPEARS. If that segment is composed of k boxes, you will get k*k points. for example, if you click on a silver box, the silver segment disappears, you got 4*4=16 points.
Now let's look at the picture below:
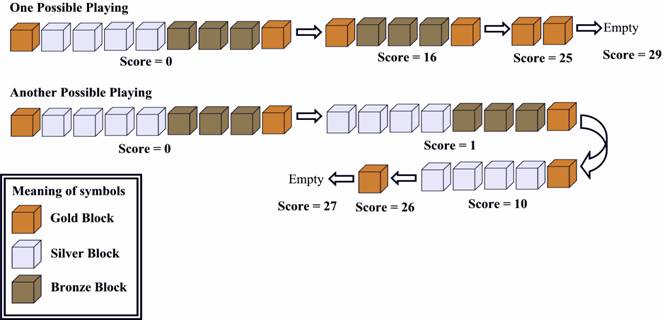
Figure 2
The first one is OPTIMAL.
Find the highest score you can get, given an initial state of this game.
The corresponding picture will be as shown below:

Figure 1
If some adjacent boxes are all of the same color, and both the box to its left(if it exists) and its right(if it exists) are of some other color, we call it a 'box segment'. There are 4 box segments. That is: gold, silver, bronze, gold. There are 1, 4, 3, 1 box(es) in the segments respectively.
Every time, you can click a box, then the whole segment containing that box DISAPPEARS. If that segment is composed of k boxes, you will get k*k points. for example, if you click on a silver box, the silver segment disappears, you got 4*4=16 points.
Now let's look at the picture below:

Figure 2
The first one is OPTIMAL.
Find the highest score you can get, given an initial state of this game.
Input
The first line contains the number of tests t(1<=t<=15). Each case contains two lines. The first line contains an integer n(1<=n<=200), the number of boxes. The second line contains n integers, representing the colors of each box. The integers are in the range 1~n.
Output
For each test case, print the case number and the highest possible score.
Sample Input
2 9 1 2 2 2 2 3 3 3 1 1 1
Sample Output
Case 1: 29 Case 2: 1
题意:给你n个给定颜色的木块,每次可以取走连续的颜色相同的一段,得到的分数为取走数目的平方,问最高得分是多少。
思路:dp[i][j][k]表示i到j的木块且后面有k个和j颜色相同的木块时的最高得分,每次转移的时候转移最后这k+1个相同的木块,去与前面的可能的情况合并。dp[l][r][k]=max(dp[l][r][k],dfs(l,i,k+1)+dfs(i+1,r-1,0))。
AC代码如下:
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,val[230],dp[230][230][230];
int dfs(int l,int r,int k)
{
if(l>r)
return 0;
if(dp[l][r][k])
return dp[l][r][k];
dp[l][r][k]=dfs(l,r-1,0)+(1+k)*(1+k);
for(int i=r-1;i>=l;i--)
if(val[i]==val[r])
dp[l][r][k]=max(dp[l][r][k],dfs(l,i,k+1)+dfs(i+1,r-1,0));
return dp[l][r][k];
}
int main()
{
int T,t,i,j,k;
scanf("%d",&T);
for(t=1;t<=T;t++)
{
scanf("%d",&n);
memset(dp,0,sizeof(dp));
for(i=1;i<=n;i++)
scanf("%d",&val[i]);
printf("Case %d: %d\n",t,dfs(1,n,0));
}
}























 1009
1009

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








