转注:
这是赵珏琼同学的复习心得。她平时学习很认真,复习时把老师讲课的内容进行汇总,尽量做到巨细无遗、准确无误,这花了她大量的时间和精力。她让我代为转贴,希望对大家的复习有所帮助。在此,对她细致而认真的汇总工作表示感谢。
原文为Word文档,其数学符号应该MathType生成的,但转贴到网上,则无法显示。这样,所有由MathType生成的符号,我都手工转换成图片形式,导致有些符号与同行文字对不齐,但这并不影响阅读和理解,如果哪位知道有好的解决办法,请告诉我。
原文档,我稍后将会放到QQ群:
交大06秋工科专业(29915490)
□未来资源(27556485)
中,如转贴文档与原文档有不同之外,一切以原文档为准。
原文档已放到网上,如下:
http://doradod.chinamofile.com/3873839906644277/8502262366585532/2/B8F5950608B03016531C35AC91106D78/离散复习.doc
复习资料汇总
(此资料仅以个人理解情况整理,如有不尽之处望大家谅解)
第一章
涉及内容:
1.1命题
1.2条件命题与逻辑等价
1.5证明
1.7数学归纳法
一.命题
1. 需理解的定义:
p和q的合取,记做
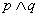 ,即命题p与q;(把
,即命题p与q;(把
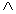 当成and中的n来记)
当成and中的n来记)
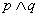 ,即命题p与q;(把
,即命题p与q;(把
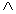 当成and中的n来记)
当成and中的n来记)
p和q的析取,记做
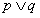 ,即命题p或q;(把
,即命题p或q;(把
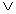 当成or中的r来记)
当成or中的r来记)
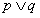 ,即命题p或q;(把
,即命题p或q;(把
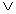 当成or中的r来记)
当成or中的r来记)
非p,记做
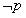 ;当p为真时
;当p为真时
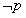 为假;
为假;
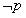 ;当p为真时
;当p为真时
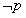 为假;
为假;
2. 题型:判断真假 写真值表
3. 合取下只有当p和q都为真时,
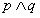 才为真;析取下只有当p和q都为假时才为假;
才为真;析取下只有当p和q都为假时才为假;
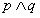 才为真;析取下只有当p和q都为假时才为假;
才为真;析取下只有当p和q都为假时才为假;
以摩根定理为例:先考虑非再考虑合取和析取,有括号优先

所以
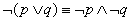 (写的时候只要把红色的写上就可以了)
(写的时候只要把红色的写上就可以了)
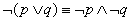 (写的时候只要把红色的写上就可以了)
(写的时候只要把红色的写上就可以了)
二.条件命题与逻辑命题
1. 需理解的定义:
如果p和q是命题,那么命题——如果p,则q称为条件命题,表示成:
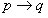 ;
;
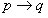 ;
;
如果命题
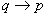 为假时,命题
为假时,命题
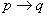 为真,称
为真,称
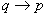 为
为
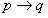 的逆命题。
的逆命题。
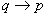 为假时,命题
为假时,命题
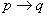 为真,称
为真,称
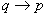 为
为
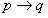 的逆命题。
的逆命题。
称
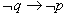 为
为
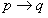 的逆否命题,当
的逆否命题,当
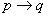 为真时,
为真时,
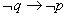 也为真。
也为真。
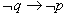 为
为
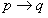 的逆否命题,当
的逆否命题,当
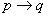 为真时,
为真时,
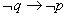 也为真。
也为真。
如果p和q是命题,则命题p当且今年当q称为双条件命题,表示成:
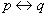 。
。
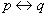 。
。
2. 题型:写真值表
3. 条件命题
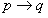 ,只有当p为真,而q为假时,
,只有当p为真,而q为假时,
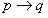 才为假,其他情况都为真。
才为假,其他情况都为真。
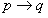 ,只有当p为真,而q为假时,
,只有当p为真,而q为假时,
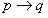 才为假,其他情况都为真。
才为假,其他情况都为真。
双条件命题
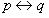 ,当p和q同时为真或同时为假时,
,当p和q同时为真或同时为假时,
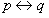 才为真。
才为真。
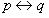 ,当p和q同时为真或同时为假时,
,当p和q同时为真或同时为假时,
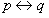 才为真。
才为真。
4. 理解以下两个真值表
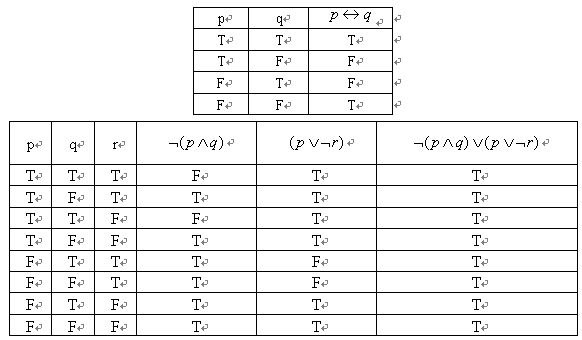
以上表格为双条件命题的真值表

以上表格为逆否命题的真值表(只需红色部分)
5.作业涉及过的内容:
第一次作业第一题
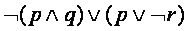 的真值表
的真值表
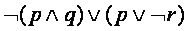 的真值表
的真值表
三.证明
1.需理解的定义:条件如果A,则B;因为B成立的,所以A是成立的。
2.考题类型:给予一个前提,要求证明结论是有效的;(同样画真值表)
3.参考以下例题
证明
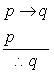

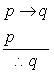

此时只参考红色部分,因为
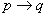 和p都为真的时候,q也为真所以结论是成立的。
和p都为真的时候,q也为真所以结论是成立的。
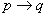 和p都为真的时候,q也为真所以结论是成立的。
和p都为真的时候,q也为真所以结论是成立的。
4.作业涉及过的内容:
第一次作业第二题
论证过程是否有效
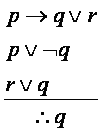
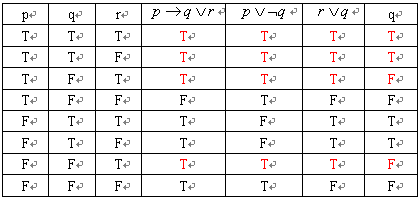
答:通过以下真值表(红色部分)可看出——当3个前提都为真时,结论q可为真也可为假;即结论q并非“必为真”,因此论证过程是无效的。
四.数学归纳法:
1. 需理解的原理:假设对于每一个正证书n,以正整数为论域的命题函数S(n);
假设
S
(
1
)为真;对任意的
n
≥
1
,如果
S
(
n
)为真,则
S
(
n+1
)为真。则对每一个正整数
n
,
S
(
n
)为真。(很重要,需记住)
2. 题型:给出过程和结论,要求给予证明;或给出过程,要求自己分析答案,再证明。
3. 解题过程:
(1) 基本步:说明如果n=1的情况,很容易做到,即写出当n=1,S(1)=?得到结论为真;
(2) 归纳步:假设对任意自然数n结论是成立的,即假设S(n)的等式或不等式是成立的,然后证明S(n+1)是成立的。
(3) 写出结论:因为基本步和归纳步都已经通过验证,所以依数学归纳法原理可以保证,对每一个正整数n,结论S(n)。。都为真。
4. 书中例题:
问题:使用数学归纳法证明对于任意n≥
1, 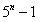 能被4整除。
能被4整除。
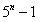 能被4整除。
能被4整除。
解题:(1)基本步:当n=1时,
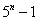 =5-1=4。可以被
4整除。
=5-1=4。可以被
4整除。
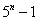 =5-1=4。可以被
4整除。
=5-1=4。可以被
4整除。
(
2)归纳步:假设 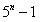 都可以被4整除,证明
都可以被4整除,证明 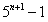 可以被4整除;
可以被4整除;
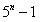 都可以被4整除,证明
都可以被4整除,证明 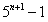 可以被4整除;
可以被4整除;
即:
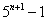 =
= 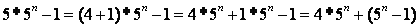
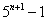 =
= 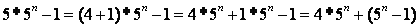
由此可以看出
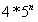 可以被4整除,而根据归纳假设
可以被4整除,而根据归纳假设 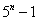 也可被4整除,
也可被4整除,
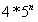 可以被4整除,而根据归纳假设
可以被4整除,而根据归纳假设 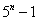 也可被4整除,
也可被4整除,
所以
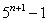 能被4整除。
能被4整除。
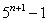 能被4整除。
能被4整除。
(
3)因为基本步和归纳步都已经通过验证,所以依数学归纳法原理可以保证,对于任意n≥
1, 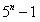 能被4整除。
能被4整除。
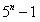 能被4整除。
能被4整除。
5.作业涉及过的内容:
第一次作业第三题:用归纳法证明:
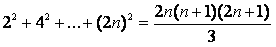
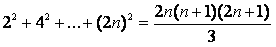
解题:(1)基本步:通过设n=1,可得
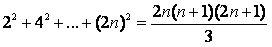 =4为真。
=4为真。
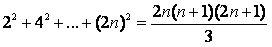 =4为真。
=4为真。
(2)归纳步:假设等式成立,即
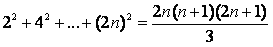 为真,必须证明n+1等式为真。
为真,必须证明n+1等式为真。
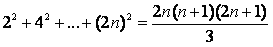 为真,必须证明n+1等式为真。
为真,必须证明n+1等式为真。
即:
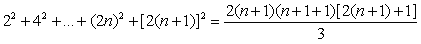 为真。
为真。
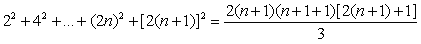 为真。
为真。
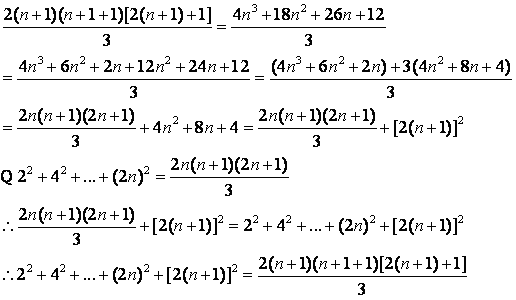
因此:
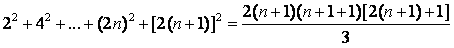 为真。
为真。
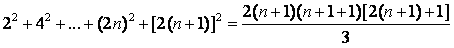 为真。
为真。
(3)因为基本步与归纳步都已经通过验证,所以,依数学归纳法原理可以保证,对每一个正整数n等式都为真。
(归纳过程中只需留下较重要的步骤即可)
第二章
涉及内容:
2.1集合
2.2函数
一.集合
1.需理解的概念:集合是一些无序的对象的全体。如果|X|=n,则|P(X)|=
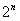 。
。
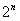 。
。
如果
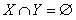 ,则称集合X和集合Y是不相交的;如果S中的任意两个不同的集合 X和Y都是不相交的,则集族S称为两两不相交的。
,则称集合X和集合Y是不相交的;如果S中的任意两个不同的集合 X和Y都是不相交的,则集族S称为两两不相交的。
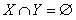 ,则称集合X和集合Y是不相交的;如果S中的任意两个不同的集合 X和Y都是不相交的,则集族S称为两两不相交的。
,则称集合X和集合Y是不相交的;如果S中的任意两个不同的集合 X和Y都是不相交的,则集族S称为两两不相交的。
有时研究的集合都是某个集合U的子集,此时U称为全集。
2.题型:给出一个集合,写出集合中元素的个数,写出所有的子集,写出集合的幂集;给出2-3集合,要求写出其并集,交集,差集等;给出2个集合,要求写出笛卡儿积;
3.如给一集合A={a,b,c},P(A)表示所有A的子集,
即:
&,{a},{b},{c},{a,b},{a,c},{b,c},{a,b,c}.
|A|表示集合中元素的个数,|A|=3。
|P(A)|表示A的幂集,|P(A)|=
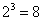 。
。
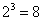 。
。
4
.典型题:
(1)P83 2.1.11——在165个学生中,8个人既学微积分和心理学又学习计算机科学;33个人既学习微积分又学习计算机科学;20个人既学习微积分又学习心理学;24个人既学习心理学又学习计算机科学;79个人学习微积分;83个人学习心理学;63个人学习计算机科学。问有多少人三门课程中一门都没有学?
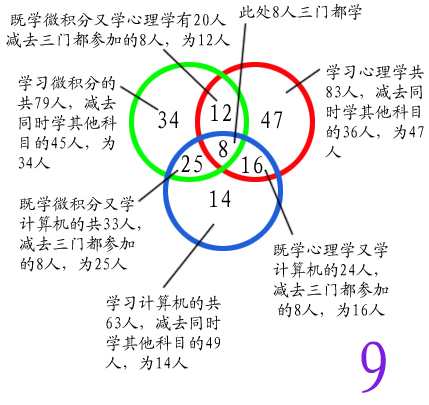
图中绿圈代表微积分,红圈代表心理学,蓝圈代表计算机科学
数字9为三门一门都没有学的同学,由165个学生中减去所得:165-34-12-8-25-16-14-47=9。
(考试所问问题可能有所不同,可根据所画出的图找出答案,如找错了,图画对也有分,所以请记清这个图是怎么画的,只要知道解决问题的方法即可)
(2)P86 2.1.15——如果X = {1,2,3},Y = {a,b},则
X * Y = {(1,a),(1,b),(2,a),(2,b),(3,a),(3,b))
Y * X = {(a,1),(a,2),(a,3),(b,1),(b,2),(b,3)}
X * X = {(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3)}
Y * Y = {(a,a),(a,b),(b,a),(b,b)}
|X * Y| = |X|*|Y|
X * Y 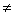 Y * X
Y * X
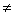 Y * X
Y * X
(由于上课时老师题到会考,所以也列入给大家参考下,只要过一遍应该就没问题了)
(3)P85 2.1.13——对i
/1,给定
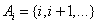 且
且
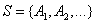 ,
,
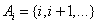 且
且
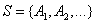 ,
,
则
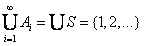 ,
,
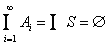
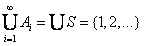 ,
,
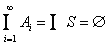
(4)P85 2.1.14——因为集合X = {1,2,3,4,5,6,7,8},中的每个元素恰属于集族
S = {{1,4,5},{2,6},{3},{7,8}}中的一个元素,所以S是X的一个划分。
(3)和(4)属于后备题,保险期间稍微看一下。
5.作业涉及过的内容:
第二次作业第一题
如果
A
= {1, 3, 4, 5, 6, 7}
,
B
= {x | x
是偶数
}
,
C
= {2, 3, 4, 5, 6}
,求
(A
∩
B
)
-
C
。
答:因为
A
∩
B=
{ 4, 6,}
,所以(A
∩
B
)
–
C= 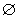
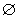
第二次作业第二题
如果
X
是一个集合且
|X| = 8
,则
(X)
有多少个成员?
X
有多少个真子集?
答:(X)有8个成员;
X
的真子集= 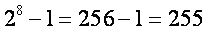 ;即X有255个真子集;
;即X有255个真子集;
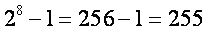 ;即X有255个真子集;
;即X有255个真子集;
(子集有256个,真子集去掉本身)
二.函数
1.需理解的定义:函数将集合X中的每一个元素指派为集合Y中
惟一的一个元素。
(对于X中的元素总有一个Y中的元素与起定义)
如果函数f的值域是Y,则称函数f为对Y映上的
如果一个函数既是一对一的又上映上的,则称这个函数为双射。
2.题型:可能为填空(概念题),问是不是函数,是不是一对一的,是不是双射,是不是映上等问题;
第三章
涉及内容:
3.1 关系
3.2 等价关系
3.3 关系矩阵
一.关系
1.集合
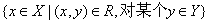 称为R的定义域。
称为R的定义域。
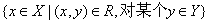 称为R的定义域。
称为R的定义域。
集合
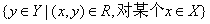 称为R的值域。
称为R的值域。
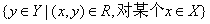 称为R的值域。
称为R的值域。
函数是一种特殊的关系。从X到Y的函数f是从X到Y的关系,并具有性质:
(1) f的定义域是X。
(2) 对每个x∈X,有惟一的y∈Y使得(x,y)∈f。
如果对每个x∈X都有(x,x)∈
R,集合X上的关系R称为
自反的。
如果对所有的x,y∈X,若(x,y)∈
R则(y,x)∈R集合X上的关系R称为
对称的。
如果对所有x,y∈X,若(x,y)∈
R且x≠y,则(y,x) 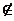 R,集合X上的关系R称为
反对称的。
R,集合X上的关系R称为
反对称的。
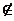 R,集合X上的关系R称为
反对称的。
R,集合X上的关系R称为
反对称的。
如果自己本身和自己都没有关系称
反自反的。
2.题型:给出集合,问关系是否是自反的,对称的,反对称的,传递的等;
3.{(1,1),(2,2),(3,3)}称为自反的
{(1,2),(2,3)}称为反自反的
{(1,2),(2,2)}称为非自反的
(反自反与非自反是不同的)(反对称与不对称也是不同的)
4.作业涉及过的内容:
第二次作业第三题
1.
如果
A
∪
B
= B
,
A
和
B
间有什么关系一定成立?
答:自反关系(因为A并B等于B,说明A=B或是B的子集,A中每个元素B中都有,所以根据定义“
如果对每个
x
∈
X
都有(
x
,
x
)
∈R,
集合
X
上的关系
R
称为自反的
。”,所以是自反关系。
二.等价关系
1.需理解的定义:自反的、对称的且传递的关系称为等价关系。
2.题型:给出一个关系,问是不是等价关系(需说明是自反的对称的传递的,再说是等价的)
3.例题:考虑{1,2,3,4,5}上的关系
R ={(1,1),(1,3),(1,5),(2,2),(2,4),(3,1),(3,3),(3,5),(4,2),(4,4),(5,1),(5,3),(5,5)}
划分{{1,3,5},{2,4}}
因为(1,1),(2,2),(3,3),(4,4),(5,5) ∈
R,所以R是自反的。而在R中有(x,y),也必定有(y,x),所以R是对称的。最后,在R中有(x,y)和(y,z),必有(x,z),所以R是传递的。因此,R是{1,2,3,4,5}上的等价关系。
(在答题过程中只要写出红色部分即可。)
4.作业涉及的内容:
第二次作业第四题
集合
{3, 2, 2}
与
{x | x
是整数且
1 < x
≤
3}
相等吗?解释原因。
答:相等的
因为,
{x | x
是整数且
1 < x
≤
3}={2,3}
,一个集合是由它的元素所决定而与描述它时列举其元素的特定顺序无关,且集合中的某些元素可以重复列举多次,但集合中只包含一个这样的元素;所以,这两个集合是相等的。
三.关系矩阵
1.需理解的定义:矩阵是一种愤怒改变地表示从X到Y的关系R的方法。
如果xRy,就令x行y列的元素为1,否则令其为0。称为关系R的矩阵。
如果矩阵从左上角开始的对角线是
1的话,那么关系是对称的。
2.题型:给出集合和关系,要求证明是对称的或自反的等等
3.例题:(已向老师提问,稍后补充)
第六章
(有
2-3
题)
涉及内容:
6.1 基本原理
6.2 排列与组合
6.6 广义的排列和组合
6.7 二项式系数和组合恒等式
6.8 鸽巢原理
一.基本原理
1.需理解的原理:乘法原理——如果一项工作需要t步完成,第一步有n
1种不同的选择,第二步有n
2种不同的选择,。。,第t步有n
t种不同的选择,那么完成这项工作所有可能的不同的选择总数为n
1*n
2*…*n
t。
加法原理——假定X
1,…,X
t均为集合,第i个集合X
i有n
i个元素。若{X
1,…,X
t}为两两不相交的集合(若X
i≠X
j,X
i∩X
j=
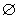 ),则可以从X
1,X
2,…,X
t)选择出元素总数为n
1+n
2+…+n
t。
),则可以从X
1,X
2,…,X
t)选择出元素总数为n
1+n
2+…+n
t。
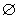 ),则可以从X
1,X
2,…,X
t)选择出元素总数为n
1+n
2+…+n
t。
),则可以从X
1,X
2,…,X
t)选择出元素总数为n
1+n
2+…+n
t。
2.乘法原理可总结为:当一项工作分为若干步时,将每一步的可选择数相乘便得到这项工作的左右可选择个数。
加法原理可总结为:当要计数的元素可分解为若干个不相交的子集时,可将每个子集元素的个数相加来得到元素的总数。
3.例题:
(1)——(a)用ABCDE五个字母可以组成多少个不重复的长度为4的字符串?
(b)(a)中有多少个字符串以字母B开头?
(c)(a)中有多少个字符串不以字母B开头?
解:(
a)为4个位置选字母,第一次有5个选择,第二次4个,第三次3个,第四次2个,所以用乘法原理,为5*4*3*2=120个字符串。
(
b)由于第一个字母为B,所以第一个位置已经设定好了,剩下3个位置从另4个字母中选择,供选择的个数分别为4、3、2,用乘法原理,为4*3*2=24个字符串。
(
c)由于已经知道所有次数和只有B开头的次数,相减即为不以B开头的次数,为120-24=96个字符串。(如用乘法原理也可计算,即第一个字母从除去B的另4个字母中选择,选去一个后,还剩下包括B在内的4个字母,故后3处仍以4、3、2的选择次数递减,为4*4*3*2=96个字符串。)
(
2)——X为n元素集合,有多少满足 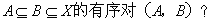
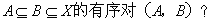
解:由于
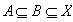 ,所以X中的元素必为A、B-A、X-B中的元素,也就把X中的元素指定到了A、B-A、X-B三种情况中,而X有n个元素,每一个元素都有可能在A、B-A、X-B这三个集合中的任意一个中,所以为3*3*…*3,有n个3,即为
3n个满足条件的有序对(
A,B)。(此题多次考过且多次有人做错,注意需理解题意,有不明白处可再参照课本P229的6.1.6)
,所以X中的元素必为A、B-A、X-B中的元素,也就把X中的元素指定到了A、B-A、X-B三种情况中,而X有n个元素,每一个元素都有可能在A、B-A、X-B这三个集合中的任意一个中,所以为3*3*…*3,有n个3,即为
3n个满足条件的有序对(
A,B)。(此题多次考过且多次有人做错,注意需理解题意,有不明白处可再参照课本P229的6.1.6)
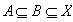 ,所以X中的元素必为A、B-A、X-B中的元素,也就把X中的元素指定到了A、B-A、X-B三种情况中,而X有n个元素,每一个元素都有可能在A、B-A、X-B这三个集合中的任意一个中,所以为3*3*…*3,有n个3,即为
3n个满足条件的有序对(
A,B)。(此题多次考过且多次有人做错,注意需理解题意,有不明白处可再参照课本P229的6.1.6)
,所以X中的元素必为A、B-A、X-B中的元素,也就把X中的元素指定到了A、B-A、X-B三种情况中,而X有n个元素,每一个元素都有可能在A、B-A、X-B这三个集合中的任意一个中,所以为3*3*…*3,有n个3,即为
3n个满足条件的有序对(
A,B)。(此题多次考过且多次有人做错,注意需理解题意,有不明白处可再参照课本P229的6.1.6)
(
3)——从5本不同的计算机书、3本不同的数学书和2本不同的艺术书中选择出不同类的两本,共有多少种选法?
解:先用乘法原理计算出分别选计算机和数学、计算机和艺术、数学和艺术
3种情况分别存在的选法,即计算机和数学=5*3=15种,计算机和艺术=5*2=10种,数学和艺术=3*2=6中;再把3种情况相加,即可得到总共有15+10+6=31种选法。
(
4)——由A、B、C、D、E和F六个人组成的委员会,要选出一个主席、一个秘书和一个出纳员。
(
a)共有多少种选法?
(
b)若主席必须从A和B中选出,共有多少种选法?
(
c)若E必须有职位,共有多少种选法?
(
d)若D和F都有职位,共有多少种选法?
解:(
a)用乘法原理,从6个人中选3个人分别担任3个职位,那么第一个职位从6个人中选,第二个职位从5个人中选,第三个职位从4个人中选,为6*5*4=120种选法。
(
b)由于主席必须从A和B中选,那么先拿出主席的职位,从A和B种选一个,有2种选法,随后的2个职位再从剩下的5个人中选,为2*5*4=40种选法。
(
c)因为必须给E一个职位,所以先让E从3个职位中选择,有3种选法,随后的2个职位从另5人中选出,为3*5*4=60种选法。
(
d)要求D和F都有职位,那么就先让D和F从3个职位中选出2个,为3*2=6种选法,剩下的1个职位从剩余的4个人中选1个,所以为6*4=24种选法。
二.排列与组合
1.需理解的定义:一组有序的对象,例如选票上的名字,称其为排列。
n个元素的排列共有n!种。
从一组对象中不计顺序的取出若干个称为组合。(无序的)
n个不同元素上的r排列数目(即从n个中选取r个元素的排列方法)为P(n,r)=n(n-1)(n-2)…(n-r+1)=
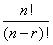 ,r≤n。
,r≤n。
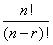 ,r≤n。
,r≤n。
n个不同元素上r组合数为
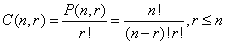
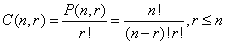
2.题型:分配职位、分配座位、分配书本等等,所有书本和作业中出现过的题。
3.例题:
(1)——ABCDEF组成的排列中,(a)有多少含有DEF的子串?(b)D、E、F三个字母相连的有多少种?
解:(
a)要求含有DEF的子串,即DEF已经排列好了,无需再动,然后把DEF看成一个成员,和A、B、C再进行排列,即第一个位置由4个中选1,第二个位置由3个中选1,以此类推,为4*3*2*1=4!=24种含有DEF的子串。
(
b)此处只要求D、E、F三个字母相连,并没要求一定按DEF的顺序排列,所以先应把D、E、F三个字母进行排列,即3*2*1=6,然后再把这6个可能性当成一个成员和剩下的3个字母排列,即4!=24种,所以总的排列方法应为6*24=144种。
(
2)——从10个人中选出一个主席、一个副主席、一个秘书和一个出纳员,共有多少种不同的选法?
解:此处是要求在
10个人中选出4个人出任4个不同的职位,所以应该是有序的排列,可用P(n,r)的公式进行,即P(10,4)= 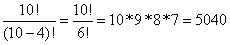 ,所以共有5040种不同的选法。(考试中只要写到10!/6!即可,不需算出结果)
,所以共有5040种不同的选法。(考试中只要写到10!/6!即可,不需算出结果)
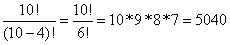 ,所以共有5040种不同的选法。(考试中只要写到10!/6!即可,不需算出结果)
,所以共有5040种不同的选法。(考试中只要写到10!/6!即可,不需算出结果)
(
3)——7个男生和5个女生站成一列,不循序两个女生站一起,工有多少种站法?
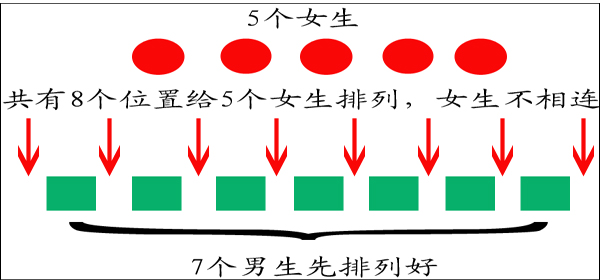 解:由于女生不能排一起,所以先把
7个男生排好,即7!=5040;由于女生不能排一起,所以现在共有8个位置供5个女生排进去,即P(8,5)=8*7*6*5*4=6720;再用乘法原理,把5040和6720相乘即可。
解:由于女生不能排一起,所以先把
7个男生排好,即7!=5040;由于女生不能排一起,所以现在共有8个位置供5个女生排进去,即P(8,5)=8*7*6*5*4=6720;再用乘法原理,把5040和6720相乘即可。
(4)——从10个人中选出一个3个人的委员会,共有多少种不同的选法?
解:由于委员会中的成员是不计次序的,所以要用C(n,r)
即:
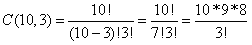 =120
=120
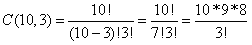 =120
=120
(5)——从5个女人和6个男人只能感选出由2个女人和3个男人组成的委员会,共有多少种选法?
解:此处委员会也不计次序,因此也要用到C(n,r)的公式,
即:
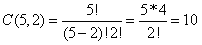
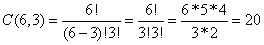
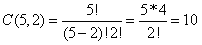
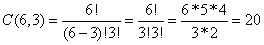
然后用乘法原理,将两数相乘为10*20=200种选法。
三.广义的排列组合
1.需理解的定义:设序列S包含n个对象,其中第1类对象有n
1个,第2类对象有n
2个,..第t类对象有n
t个。则S的不头脑感排序个数为
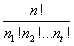
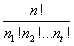
X为包含t个元素的集合,在X中允许重复、不计顺序地选取k个元素,共有C(k+t-1,t-1)=C(k+t-1,k)种选法。
2.题型:给出有几个重复的字母问有几种排列方法,给出若干本相同内容但类别不同的书要求分派等;
3.例题:
(1)——用下面几个字母可以组成多少个字符串?M I S S I S S I P P I
解:由于有重复的字母,可以考虑先把相同的一一陪列进11个不同的位置,而相同的排前排后都一样,所以是无序的,用C(n,r)公式,如此,排列掉几个可以从n中见去几个,最后用乘法原理将其相乘;以I、S、P、M的顺序为例可如下排列:
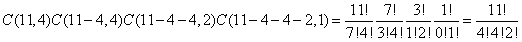
(2)——有一本计算机科学书、一本物理书和一本历史书,图书馆对每一本书都至少存有6个副本。从中选取6本,共有多少种不同的选法。
解:问题相当于从集合(计算机科学,物理,历史)中允许重复、不计顺序地选取6个。选法由不同类书的数量惟一确定。例如可选择:
计算机科学
物理
历史
XXX | XX | X
即选择3本计算机科学书、2本物理书和1本历史书,又例如可以选择
计算机科学
物理
历史
| XXXX | XX
即选择4本物理书和2本历史书,不选择计算机科学书。可见6个“X”和2个“|”的每个排列对应一个选择,所以可将本题化为排序的计数问题,共有C(8,2)=28种方法从8个可能的位置中选出2个作为“|”的位置。所以工有28种方法选出6本书。
(本题用到第
2
种定义)
(3)——设有一堆红色球,一堆蓝色球和一堆绿色球,每一堆都不少于8个。
(a)从中选出8个,共有多少种不同的选法?
(b)从中选出8个,要求每种颜色的球至少一个,共有多少种不同的选法?
解:(a)运用定理,了解到本题是需要把8个“X”和3-1个“|”填入到8+3-1个空处,所以得到C(8+3-1,3-1)=C(10,2)=45种选法。
(b)题中要求至少每种颜色选取一个,那么先各选出3个球,然后剩余的5个球再在3种颜色中进行选择,即把5个“X”和3-1个“|”填入5+3-1个空处,所以得到C(5+3-1,3-1)=C(7,2)=21种选法。
(本题用到第
2
种定义)
(4)——12本相同的书分给A、B、C和D4个学生,共有多少种分法?
解:本题需要看成把12本书分到A、B、C、D4个名字上,即把12个“X”和4-1个“|”填图12+4-1个空处,所以得到C(12+4-1,4-1)=C(15,3)=455种选法。
(本题用到第
2
种定义)
(5)——(a)方程
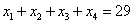 有多少非负整数解?
有多少非负整数解?
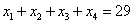 有多少非负整数解?
有多少非负整数解?
(b)方程
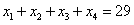 有多少满足x
1>0、x
2>1、x
3>2、x
4≥0的整数解?
有多少满足x
1>0、x
2>1、x
3>2、x
4≥0的整数解?
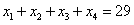 有多少满足x
1>0、x
2>1、x
3>2、x
4≥0的整数解?
有多少满足x
1>0、x
2>1、x
3>2、x
4≥0的整数解?
解:(a)由于需要非负整数解,那就需要将29可重复且无序的分派到4个x中,运用定义可知即是把29个“X”和4-1个“|”填图29+4-1个空处,所以得到C(29+4-1,4-1)=C(32,3)=4960种选法。
(b)如题要求,即可先从29中分别取1给x
1、取2给x
2、取3给x
3及取0给x
4;此时只剩
29-1-2-3=23个数可以分配给4个x,运用定义可知即是把23个“X”和4-1个“|”填图23+4-1个空处,所以得到C(23+4-1,4-1)=C(26,3)=2600种选法。
4.作业涉及的内容:
第三次作业第一题
:排列字母ILLINOIS可以得到多少个不同的字符串?
答:考虑到含有重复的字母,依次为同一种字母选定位置,有3个I字母,所以得到C(8,3);有2个L字母,所以得到C(8-3,2);分别有1个N字母、1个O字母和1个S字母,得到C(8-3-2,1)、C(8-3-2-1,1)和C(8-3-2-1-1,1);
所以最后为:C(8,3)C(5,2)C(3,1)C(2,1)C(1,1)= 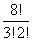 =3360
=3360
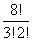 =3360
=3360
所以可以得到3360个不同的字符串。
第三次作业第二题
:排列字母ILLINOIS,要求某个I排在某个L之前,可以得到多少个不同的字符串?
答:首先求所有L都在I之前的情况,即先选定N、O、S的位置(因为3个字母各不同,此处为有序排列,即用P(n,r)公式),再插入L和I,插入N、O、S后只剩5个位置,而需要L都在I前只有一种可能,所以L都在I前的字符串个数为P(8,3)=8*7*6=336;再用总的字符串数减去L都在I前的字符串数即可得某个I排在某个L之前的字符串数;
所以应为: 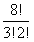 -336=3360-336=3024
-336=3360-336=3024
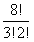 -336=3360-336=3024
-336=3360-336=3024
所以可以得到3024个不同的字符串。
第三次作业第三题
:将12本不同的书分给4个学生,每人分得3本,共有多少种不同分法?
答:既然每人要得3本,就依次分别选3本,共选4次
即:C(12,3)C(12-3,3)C(12-3-3,3)C(12-3-3-3,3)
= 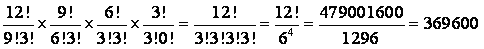
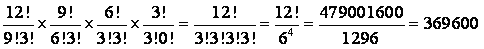
所以共有369600种不同分法。
第三次作业第四题
:方程
x1+x2+x3+x4=17
,有多少满足
x1
≥0、
x2
≥1、
x3
≥2、
x4
≥3的整数解?
答:由于需要
满足
x1
≥0、
x2
≥1、
x3
≥2、
x4
≥3,所以先赋给
x21
的值,
赋给
x32
的值,
赋给
x43
的值,那么只有
17-1-2
-3=11
个元素可以任意选择,所以根据定理可以得到
C
(
11+4-1
,
4-1
)
=C
(
14
,
3
)
= 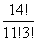 =364
=364
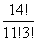 =364
=364
所以有364个满足x1≥0、x2≥1、x3≥2、x4≥3的整数解。
四.二项式系数和组合恒等式
1.需理解的定义:
二项式定理——设a和b为实数,n为正整数
则:
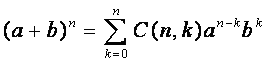
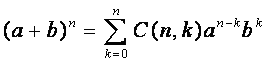
2.题型:给出(a+b+c)的n次式,要求写出某一项的系数。
3.例题:
(1)——求
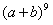 展开式中
展开式中
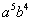 项的系数
项的系数
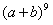 展开式中
展开式中
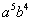 项的系数
项的系数
解:在二项式中令n=9,k=4;得C(9,4)
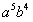 =126
=126
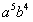 ;故
;故
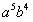 的系数为126。
的系数为126。
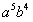 =126
=126
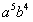 ;故
;故
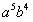 的系数为126。
的系数为126。
(2)——求
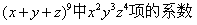
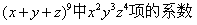
解:在9项中2次选x,3次选y,4次选z;选2次x共有C(9,2)种方法,选定x后,选3项y共有C(7,3)种选法,选定y后剩余的4项为z,即:
C(9,2)C(7,3)=1260
故
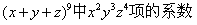 为1260。
为1260。
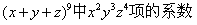 为1260。
为1260。
五.鸽巢原理
1. 需理解的定义:
原理一:n只鸽子飞入k个鸽巢,k<n,则必存在某个鸽巢包含至少两只鸽子。
原理二:设f为有限集合X到有限集合Y的函数,且|X|>|Y|,则必存在
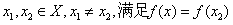 。
。
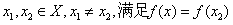 。
。
原理三:设f为有限集合X到有限集合Y上的函数,|X|=n,|Y|=m。令k=[n/m],则至少存在k个元素
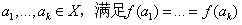 。
。
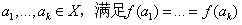 。
。
2. 题型:给出数据要求证明
(要自己判别是哪种原理且分辨什么代表鸽什么代表巢)
3. 例题:
(1)——10个人,姓为L、M、N,名为A、B、C,证明至少有两个人同名同姓。
解:先利用乘法原理得知这10个人的姓名共有3*3=9种可能性,然后将10个人看成鸽子,姓名看成鸽巢,将为人指定姓名看成鸽子飞入鸽巢。根据原理一可知,至少有两个人是同名同姓。
(2)——证明从编号1-300的计算机科学课程中选取151门不同的编号的,至少有两门编号相连。
解:设选出的课程编号为:c
1,c
2,…,c
151及c
1+1,c
2+1,…,c
151+1共有302个数字,而取值在1-301内。根据原理二,1-301为鸽子,1-300为鸽巢,|X|>|Y|,故必有2个数字是相同的,但是此处c
1,c
2,…,c
151互不相同,推断出c
1,c
2,…,c
151中的数字必有一个和c
1+1,c
2+1,…,c
151+1中的一个数字相同。
即c
i=c
j+1,表明有2个课程是相邻的。
(3)——平均灰度是黑白图象的重要属性。若两幅黑白图象的平均灰度差不超过给定的值,则称这两幅黑白图象相似。可证明在6张黑白图象中,至少有3幅图象两两相似,或至少有3幅图象两两不相似。
解:6幅图象分别为P
1,P
2,。。。,P
6。有以下5个二元组——
(P
1,P
2),(P
1,P
3),(P
1,P
4)(P
1,P
5)(P
1,P
6)
取值为“相似”或“不相似”。根据定理三,至少有[5/2]=3个二元组取值相同。设三个二元组(P
1,P
i),(P
1,P
j),(P
1,P
k)取值相同。不妨设这三个二元组取值为“相似”,若二元组(P
i,P
j),(P
i,P
k),(P
j,P
k)中有一个取值为“相似”,则对应的两幅图像与P
1为三幅两两相似的图象;否则,(P
i,P
j),(P
i,P
k),(P
j,P
k)中有一个取值为“不相似”,则P
i,P
j,P
k为两两不相似的图象。
第七章
涉及内容:
7.2 求解递归关系
一.求解递归关系
1.需理解的定义:利用迭代法求解序列
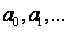 的递归关系时,先根据递归关系用
的递归关系时,先根据递归关系用
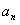 前面的
前面的
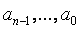 若干项表示
若干项表示
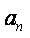 。然后反复利用递归关系将
。然后反复利用递归关系将
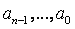 替换,直至得到
替换,直至得到
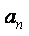 的显式公司。
的显式公司。
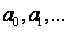 的递归关系时,先根据递归关系用
的递归关系时,先根据递归关系用
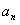 前面的
前面的
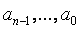 若干项表示
若干项表示
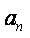 。然后反复利用递归关系将
。然后反复利用递归关系将
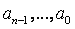 替换,直至得到
替换,直至得到
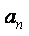 的显式公司。
的显式公司。
令
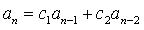 为常系数二阶齐次线性关系。若S和T为
为常系数二阶齐次线性关系。若S和T为
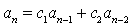 解,则U=bS+dT也为
解,则U=bS+dT也为
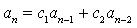 的解。若r为方程
的解。若r为方程
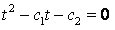 的一个根,则序列
的一个根,则序列
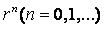 为
为
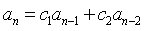 的一个解。若a为
的一个解。若a为
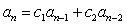 定义的序列,
定义的序列,
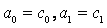 且
且
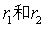 为方程
为方程
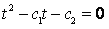 的根,
的根,
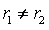 。则存在常数b和d,使得
。则存在常数b和d,使得
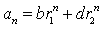 ,n=0,1,。。。成立。
,n=0,1,。。。成立。
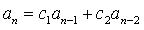 为常系数二阶齐次线性关系。若S和T为
为常系数二阶齐次线性关系。若S和T为
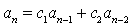 解,则U=bS+dT也为
解,则U=bS+dT也为
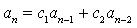 的解。若r为方程
的解。若r为方程
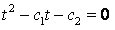 的一个根,则序列
的一个根,则序列
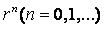 为
为
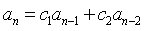 的一个解。若a为
的一个解。若a为
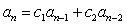 定义的序列,
定义的序列,
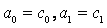 且
且
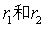 为方程
为方程
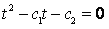 的根,
的根,
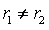 。则存在常数b和d,使得
。则存在常数b和d,使得
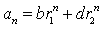 ,n=0,1,。。。成立。
,n=0,1,。。。成立。
2.题型:解一方程
3.例题:
(1)——种群数目增长
设在n=0时刻某地有200头鹿,n=1时刻有220头鹿。n-1时刻到n时刻鹿增长的数目是n-2时刻到n-1时刻鹿增长数目的两倍。给出定义n时刻鹿数目的递归关系和初始条件,然后求解递归关系。
解:令
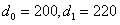
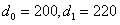
n-1时刻到n时刻鹿增长的数目为
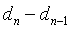 ,n-2时刻到n-1时刻鹿增长的数目为
,n-2时刻到n-1时刻鹿增长的数目为
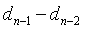 ;得递归关系为
;得递归关系为
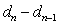 =2(
=2(
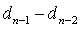 )=
)=
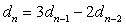
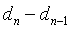 ,n-2时刻到n-1时刻鹿增长的数目为
,n-2时刻到n-1时刻鹿增长的数目为
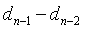 ;得递归关系为
;得递归关系为
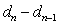 =2(
=2(
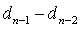 )=
)=
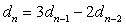
运用定义得
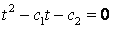 此处为:
此处为:
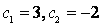 ;即
;即
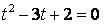 。解出得到2个根分别为1和2;再根据
。解出得到2个根分别为1和2;再根据
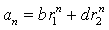 可得
可得
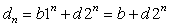 ;
;
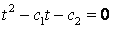 此处为:
此处为:
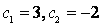 ;即
;即
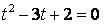 。解出得到2个根分别为1和2;再根据
。解出得到2个根分别为1和2;再根据
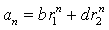 可得
可得
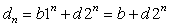 ;
;
由于本题初始条件为
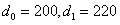 ;故得到
;故得到
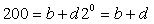 、
、
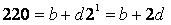 ;解此方程可得b=180,d=20;则再根据先前的
;解此方程可得b=180,d=20;则再根据先前的
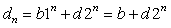 可得出
可得出
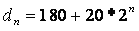 ;此即为本题递归关系。
(本题是老师拿出举例说明的,务必搞请里面的关系)
;此即为本题递归关系。
(本题是老师拿出举例说明的,务必搞请里面的关系)
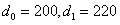 ;故得到
;故得到
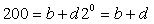 、
、
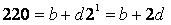 ;解此方程可得b=180,d=20;则再根据先前的
;解此方程可得b=180,d=20;则再根据先前的
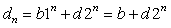 可得出
可得出
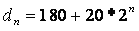 ;此即为本题递归关系。
(本题是老师拿出举例说明的,务必搞请里面的关系)
;此即为本题递归关系。
(本题是老师拿出举例说明的,务必搞请里面的关系)
(2)——求解递归关系
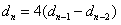 ,初始条件为
,初始条件为
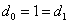 。
(需结合书
P307
)
。
(需结合书
P307
)
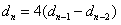 ,初始条件为
,初始条件为
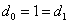 。
(需结合书
P307
)
。
(需结合书
P307
)
解:因为
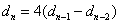 ,可得到
,可得到
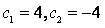 ;即
;即
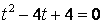 ;可得到
;可得到
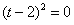 ;——
;——
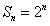 ,由于2是方程的重根,
,由于2是方程的重根,
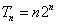 也是其解;化为一般解形为U=aS+bT;由初始条件
也是其解;化为一般解形为U=aS+bT;由初始条件
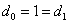 得到
得到
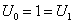 ;
;
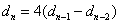 ,可得到
,可得到
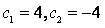 ;即
;即
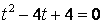 ;可得到
;可得到
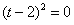 ;——
;——
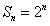 ,由于2是方程的重根,
,由于2是方程的重根,
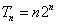 也是其解;化为一般解形为U=aS+bT;由初始条件
也是其解;化为一般解形为U=aS+bT;由初始条件
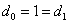 得到
得到
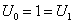 ;
;
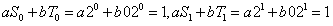 ;解得:
;解得:
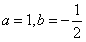 。
。
所以得到U=aS+bT——
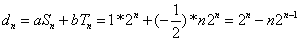
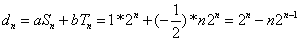
第八章
涉及内容:
8.2 路径和回路
8.3 Hamilton回路和旅行商问题
8.4 最短路径算法
8.5 图的表示
8.7 平面图
一.路径和回路(没空可不看,概念稍微过一下即可)
1.需理解的定义:
度是偶数的肯定是欧拉回路。(要考)
连通图是指从任意一个顶点开始有可以到达任意另外一个顶点的路径的图。
简单路径是从一个顶点到另一个顶点的、不存在重复出现顶点的路径。
回路是一条从一个顶点回到这个顶点的、长度非0的、不存在重复出现边的路径。
简单回路是一条从一个顶点回到这个顶点,其中除了开始和结束的顶点之外,不存在重复出现的顶点。
如果一个图中存在Euler回路,那么图是连通的,并且每个顶点的度为偶数。反之,如果一个图是连通图,并且每个顶点的度为偶数,那么图中就存在一个Euler回路。
如果G是一个m条边和n个顶点{v
1,v
2,..,v
n}的图,那么
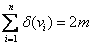 ,(度之和为2m);特别是,一个图中所有顶点的度之和为偶数。
,(度之和为2m);特别是,一个图中所有顶点的度之和为偶数。
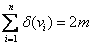 ,(度之和为2m);特别是,一个图中所有顶点的度之和为偶数。
,(度之和为2m);特别是,一个图中所有顶点的度之和为偶数。
任意图里,奇数度的顶点个数为偶数。
如果图G中存在一条从v到v的 回路,那么G中含有一条从v到v的简单回路。
2.题型:给一图,问是否存在欧拉回路,如存在把它画出来(即按边和节点的遍历次序将其写出来)。
可能会给出路径,然后要求判断是否是简单路径、环路或简单回路。
3.是简单路径就一定不是环路和简单回路,不是环路必定不是简单回路;是环路未必是简单回路。
4.例题:问此图有无欧拉回路,有则画出。(从任何一点皆可)

二.Hamilton回路和旅行商问题
1.需理解的定义:称图G中一条包含除出发和结束的顶点出现两次外其他所有顶点恰出现一次的回路为Hamilton回路;
2.题型:给出一图,要求画出Hamilton回路;或问什么叫Hamilton回路。
3.Hamilton回路不存在简单的判别条件。
三.最短路径算法
1.需理解的定义:在一个连通的带权图中找从顶点a到顶点z的最短路径的长度。
2.题型:给出一个图,要求找出最短路径,并描述找的过程(即先找哪个节点再找哪个节点)
3.例题:要求写出此的最短路径的长度,并描述过程
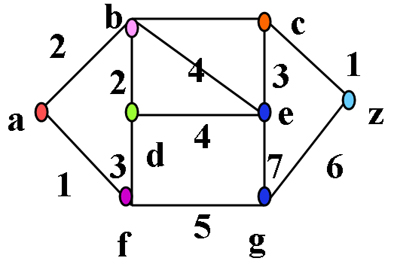
解答:最短路径的长度为5,且最短路径是(a,b,c,z)。
四.图的表示
1.用来表示图的首选方法是邻接矩阵。
2.题型:给出一个图或矩阵,问是不是存在欧拉回路。(把矩阵中的数相加,偶数就是欧拉回路,奇数就不是欧拉回路。
五.平面图
1.需记住的公式:
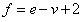 (此公式针对连通图才成立)
(此公式针对连通图才成立)
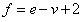 (此公式针对连通图才成立)
(此公式针对连通图才成立)
2.f表示面的数目,e表示边的数目,v表示顶点的数目。
3.题型:不确定,可能给出一个图球面的数目等。
第九章
涉及内容:
9.1 简介
9.4 最小生成树
9.5 二叉树
9.6 树的遍历
一.简介
1.需理解的定义:Huffman树P395(可以看一下,没有明确定义)
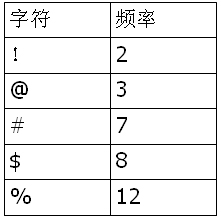
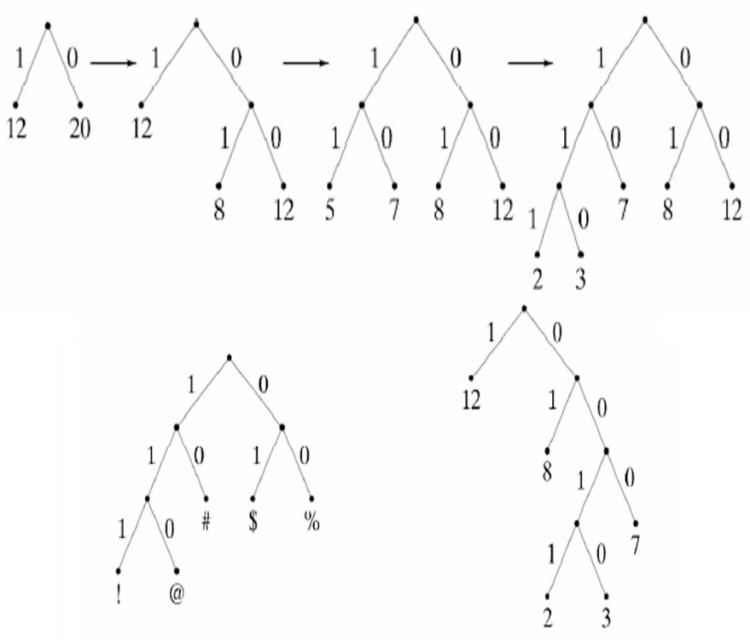
2.题型:给出字符和频率,要求把树构造出来(每一步写出来)
3.从最小的开始对应过程进行构造。
4.例题:参照给出的字符和频率构造一个油画的Huffman编码。
二.最小生成树
1.需理解的定义:图必须是生成树(包含所有顶点),必须是连通的,并且两两顶点之间必须是单一简单路径,因此而使生成树的权值最小,这样的树叫做最小生成树。
2.题型:给定一个图,要求画出最小生成树(写出过程更容易给分)
三.二叉树
1.需理解的定义:二叉树的每个顶点最多有两个子节点,而且每个子节点不是左子节点就是右子节点,每个顶点的子节点的可能个数为0、1、2。Huffman编码树是一棵二叉树。从一个顶点移动到它的左子节点代表比特1,如果移动到右子节点则代表比特0。
如果T是有i个内部顶点的满二叉树,则T有i+1个叶顶点,即共有2i+1个顶点。
四.树的遍历
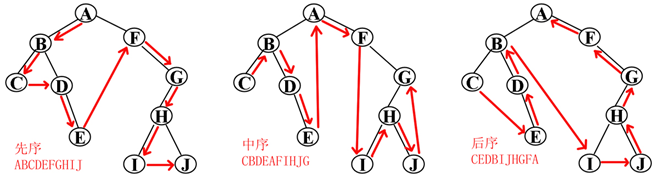
1.需理解的定义:先序——首先是根节点,然后左节点,最后右节点;
中序——先左节点,然后根节点,最后右节点;
后序——先左节点,然后右节点,最后根。
先序表达式—— —
*+ABC
/DE;(先红色部分运算成一个数字,然后再把A和B的相加数同C相乘,最后把A和B的相加数同C相乘的积同DE的商相减;即用两数前的符号进行计算)
中序表达式——(((A+B)*C)— (D/E));(先计算括号里的,展开)
后序表达式——AB+C*DE/—。(即用两数后面的符号进行计算)
2.题型:给出一个已画好的二叉树,要求用先序、中序或后序的遍历把节点处理顺序写出。
3.在中序中,要求每个节点都先左后中再右,如无右,中则为最后一个;
在后续中,要求在每个子节点处也遵循先左后右再中的遍历顺序。
4. 例题:依照所给出的图,用先序、中序或后序的遍历把节点处理顺序写出。
第十章
涉及内容:
10.2 最大流算法
一.最大流算法
1.题型:给出一个图,要求找出最大流。(写出各条路径及最后的流量数)
(给出的图应该只有黑线部分,红蓝绿三色作为解题的参考)
解:第一条线路为:a——b——c——z
{(3,2)(2,2)(4,2)}
第二条线路为:a——d——e——z
{(5,2)(2,2)(4,2)}
第三条线路为:a——d——c——z
{(5,2)(2,2)(4,2)}
三条线路的流量都为2,且各条没有超过最大限制,所以相加后最大流为6。
(以上回答方法只是参照个人理解)






















 3125
3125











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








