03-1. 二分法求多项式单根
二分法求函数根的原理为:如果连续函数f(x)在区间[a, b]的两个端点取值异号,即f(a)f(b)<0,则它在这个区间内至少存在1个根r,即f(r)=0。
二分法的步骤为:
- 检查区间长度,如果小于给定阈值,则停止,输出区间中点(a+b)/2;否则
- 如果f(a)f(b)<0,则计算中点的值f((a+b)/2);
- 如果f((a+b)/2)正好为0,则(a+b)/2就是要求的根;否则
- 如果f((a+b)/2)与f(a)同号,则说明根在区间[(a+b)/2, b],令a=(a+b)/2,重复循环;
- 如果f((a+b)/2)与f(b)同号,则说明根在区间[a, (a+b)/2],令b=(a+b)/2,重复循环;
本题目要求编写程序,计算给定3阶多项式f(x)=a3x3+a2x2+a1x+a0在给定区间[a, b]内的根。
输入格式:
输入在第1行中顺序给出多项式的4个系数a3、a2、a1、a0,在第2行中顺序给出区间端点a和b。题目保证多项式在给定区间内存在唯一单根。
输出格式:
在一行中输出该多项式在该区间内的根,精确到小数点后2位。
输入样例:3 -1 -3 1 -0.5 0.5
输出样例:0.33
这一题在当初学计算方法这门课就已经做过。(话说这一题和树有什么关系 =_=) 题目已经保证了一定有唯一一个解,所以只需要按题中所述的步骤来就可以了。可能有些人对精度的确定不是很清楚,这里简单说明一下。此题中要求结果保留到小数点后两位,而第三位数会对第二位数造成舍入误差。因此只要保证近似解的小数点后第三位数和精确解的一样就可以了。假设方程的精确解为x0,我们求出来的近似解为x,那么应该有 |x-x0|<0.001。所以当最后求解的区间满足 b-a<0.001 时,就可以满足精度要求。另外如果在二分的某一过程中刚好得到 x=x0 ,那么就直接求出了精确解。在C++中,同时使用 cout.setf(ios::fixed) 和 cout.precision(2) 可以使用输出的浮点数保留到小数点后两位。下面是完整的代码:
#include <iostream>
using namespace std;
float a3, a2, a1, a0;
const float delta = 0.001;
float f( float x )
{
float f = ((a3*x + a2)*x + a1)*x + a0;
return f;
}
int main()
{
float a, b;
cin >> a3 >> a2 >> a1 >> a0 >> a >> b;
float x0, x;
while( b-a >= delta )
{
x = (a+b)/2;
if( f( x ) == 0 )
break;
else if( f(a) * f(x) < 0 )
b = x;
else
a = x;
}
cout.setf(ios::fixed);
cout.precision(2);
x = (a+b)/2;
cout << x;
return 0;
}
03-2. List Leaves
Given a tree, you are supposed to list all the leaves in the order of top down, and left to right.
Input Specification:
Each input file contains one test case. For each case, the first line gives a positive integer N (<=10) which is the total number of nodes in the tree -- and hence the nodes are numbered from 0 to N-1. Then N lines follow, each corresponds to a node, and gives the indices of the left and right children of the node. If the child does not exist, a "-" will be put at the position. Any pair of children are separated by a space.
Output Specification:
For each test case, print in one line all the leaves' indices in the order of top down, and left to right. There must be exactly one space between any adjacent numbers, and no extra space at the end of the line.
Sample Input:8 1 - - - 0 - 2 7 - - - - 5 - 4 6Sample Output:
4 1 5
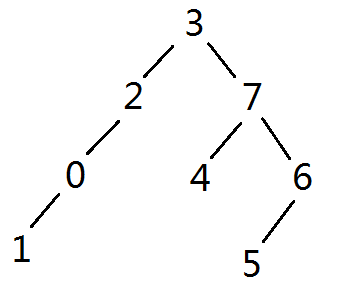
这是综合性比较强的一题,把二叉树和队列的操作都结合起来了。当然这个问题并不复杂,不过关键在于理解题意如何构建二叉树。在输入样例中,有8组数据,它们分别依次这8个节点的左孩子和右孩子。例如,对于第0组数据 1 - ,它表示节点0有左孩子1而没有右孩子。再例如,对于最后一行数据,它表示节点7有左孩子4和右孩子6。所以很明显的是,根节点肯定不会出现在上面的数据中,因为根节点不是其它任何节点的孩子。对于这个例子来说,根节点就是3。所以我们可以还原此二叉树,结果如下:
用代码实现时,需要先找到根节点(没出现过的那个数字就是根节点),再依次递归地构建其左子树和右子树。二叉树建好后,再按层序的方式输出叶节点(没有孩子的节点)。至如何层序输出,何老师说了,可以队列来实现。这里要求只输出叶节点,所以需要加一个判断条件,当其左孩子和右孩子都为空时才输出。
由于建树的过程是不能按照输入数据的顺序来的,所以我先把它存在一个数组 rec 中记录下来。在读入数据的同时也同时设置一个检查数组 check 来记录输入中有哪些数字,以方便后面寻找根节点。建完树后,再借助队列按层序的方式输出叶节点就完成了。最后的最后,要记得把 new 出来的数组给 detele 掉,不要像我这样经常忘记 +_+ ... 下面是完整的代码:
#include <iostream>
#include <string>
using namespace std;
struct record
{
int left;
int right;
};
struct node //二叉树结点
{
int num;
node* left;
node* right;
};
struct alline //队列结点
{
node* tr;
alline* next;
};
void intoAlline(node* tr, alline* &front, alline* &rear) //入队
{
if( rear )
{
rear->next = new alline;
rear = rear->next;
rear->tr = tr;
rear->next = nullptr;
}
else
{
front = new alline;
rear = front;
rear->tr = tr;
rear->next = nullptr;
}
}
void outAlline(alline* &front, alline* &rear ) //出队
{
if( front )
{
if( front->next )
{
alline* temp = front->next;
delete front;
front = temp;
}
else
{
delete front;
front = nullptr;
rear = nullptr;
}
}
}
void buildTree(record* rec, int root, node* &nodep)
{
nodep = new node;
nodep->num = root;
nodep->left = nullptr;
nodep->right = nullptr;
//--建左边的子树--
if( rec[root].left != -1 )
{
nodep->left = new node;
buildTree( rec, rec[root].left, nodep->left );
}
else
nodep->left = nullptr;
//--建右边的子树--
if( rec[root].right != -1 )
{
nodep->right = new node;
buildTree( rec, rec[root].right, nodep->right );
}
else
nodep->right = nullptr;
}
void printLeaves(node* nodep)
{
if( !nodep ) return;
alline* front; alline* rear;
front = nullptr;
rear = nullptr;
intoAlline( nodep, front, rear );
bool isFirst = true;
while( front )
{
if( !front->tr->left && !front->tr->right )
{
if( isFirst )
{
cout << front->tr->num;
isFirst = false;
}
else
cout << ' ' << front->tr->num;
}
if( front->tr->left )
{
intoAlline( front->tr->left, front, rear );
}
if( front->tr->right )
{
intoAlline( front->tr->right, front, rear );
}
outAlline( front, rear );
}
}
int main()
{
int n;
char ch;
cin >> n;
record* rec = new record [n];
int* check = new int [n];
//--将数据读入数组中记录下来---
for( int i=0; i<n; ++i )
{
ch = cin.peek();
while( ch==' ' || ch=='\n' )
{
cin.get( ch );
ch = cin.peek();
}
if( ch!='-' )
{
cin >> rec[i].left;
check[rec[i].left] = 1;
}
else
{
cin >> ch;
rec[i].left = -1;
}
ch = cin.peek();
while( ch==' ' || ch=='\n' )
{
cin.get( ch );
ch = cin.peek();
}
if( ch!='-' )
{
cin >> rec[i].right;
check[rec[i].right] = 1;
}
else
{
cin >> ch;
rec[i].right = -1;
}
}
//=======================================
//---先找到根结点---
int root=-1;
for( int i=0; i<n; ++i )
{
if( check[i] != 1 )
{
root = i;
break;
}
}
if( root==-1 ) return 0;
//---建树----
node* nodep = nullptr;
buildTree( rec, root, nodep );
//---输出叶子---
printLeaves( nodep );
delete [] rec;
delete [] check;
return 0;
}
03-3. Tree Traversals Again
An inorder binary tree traversal can be implemented in a non-recursive way with a stack. For example, suppose that when a 6-node binary tree (with the keys numbered from 1 to 6) is traversed, the stack operations are: push(1); push(2); push(3); pop(); pop(); push(4); pop(); pop(); push(5); push(6); pop(); pop(). Then a unique binary tree (shown in Figure 1) can be generated from this sequence of operations. Your task is to give the postorder traversal sequence of this tree.

Input Specification:
Each input file contains one test case. For each case, the first line contains a positive integer N (<=30) which is the total number of nodes in a tree (and hence the nodes are numbered from 1 to N). Then 2N lines follow, each describes a stack operation in the format: "Push X" where X is the index of the node being pushed onto the stack; or "Pop" meaning to pop one node from the stack.
Output Specification:
For each test case, print the postorder traversal sequence of the corresponding tree in one line. A solution is guaranteed to exist. All the numbers must be separated by exactly one space, and there must be no extra space at the end of the line.
Sample Input:6 Push 1 Push 2 Push 3 Pop Pop Push 4 Pop Pop Push 5 Push 6 Pop PopSample Output:
3 4 2 6 5 1
这一题姥姥说不用建树,那样很麻烦,可以根据输入数据得到中序遍历和先序遍历的数组,进而可以得到后序遍历的数组。但是我觉得这样做反而麻烦……我就是用建树的方法来做的。以题中的例子来说明,节点数一共有6个,那么Push和Pop操作一定分别有6次。对于每一次Push,都要新建一个节点,建完之后再去左孩子那里,然后去右孩子那里;对于每一次Pop,如果当前在左孩子这,就到右孩子那里,否则就返回到父结点。这是用递归方法来实现的。由于所有的Push和Pop操作完成时并不能退出递归,所以我添加一个计数,当操作次数达到2N次时(在这个例子中是12次),就直接退出递归。
下面是完整的代码:
#include <iostream>
#include <string>
using namespace std;
int nodes, k=0;
bool firstPrint = true;
struct binTree
{
int num;
binTree* left;
binTree* right;
};
void buildTree( binTree* &root )
{
//--把数字存入当前结点中--
root = new binTree;
cin >> root->num;
root->left = nullptr;
root->right = nullptr;
//---检查下一个操作---
string str;
cin >> str; ++k;
if( k>=2*nodes ) return;
if( str=="Push" )
{
buildTree( root->left );
if( k>=2*nodes ) return;
}
cin >> str; ++k;
if( str=="Push" )
{
buildTree( root->right );
if( k>=2*nodes ) return;
}
}
void printTree( binTree* &root )
{
if( root->left )
printTree( root->left );
if( root->right )
printTree( root->right );
if( firstPrint )
{
cout << root->num;
firstPrint = false;
}
else
cout << ' ' << root->num;
}
int main()
{
cin >> nodes;
if( nodes==0 ) return 0;
binTree* tree;
string str;
cin >> str;
++k;
if( str=="Push" )
buildTree( tree );
printTree( tree );
return 0;
}





















 764
764

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








