本文详细介绍了Jiles-Atherton磁滞模型，包括模型的简介、推导过程、MATLAB程序编写以及参数辨识。通过模型参数的智能优化算法辨识，实现了与实验数据的良好拟合。
一、J-A模型简介
Jiles-Atherton磁滞模型（J-A模型）是一种被广泛使用的磁滞模型，D.Jiles 和D.L.Atherton两位学者于1984年共同提出。该模型是一种基于软磁材料在磁化过程中的能量守恒而推导出的具有一阶常微分方程形式的磁滞模型。
J-A模型的特点：
优点：
1.模型用一阶微分方程形式表示，模拟磁性材料磁滞特性速度快，可以较好的与其他软件兼容。
2. 模型的参数较少，从而可以通过这些参数建立磁滞与温度、应力、磁化方向等因素的关系。
3. 经典J-A模型为正模型（输入变量为磁场强度H），但是它的逆模型（输入变量为磁感应强度B）容易生成，逆模型也是一个一阶微分方程。
缺点
1.J-A模型是存在很多假设，因此其在实际磁性材料的磁滞特性的模拟中会出现很多非物理的现象，如在磁化反转点后出现负斜率的磁导率、小磁滞回环模拟精度较低且不闭合的现象等等。
2.J-A模型属于历史独立型（history-independent）的磁滞模型,只具有局部记忆性，不能保留磁化历史，没有任何缓和曲线的选择而只能立刻指向主回路的正负方向的尖端。这就会导致在第一次遍历后有不闭合的小回路，如果这个磁化过程是以小磁滞回环为特点的，那么将最终导致对损耗的低估。
3。由于其属于history-independent model，当外加磁场在固定值之间震荡时，小磁滞回环将会发生严重的漂移。
二、J-A模型的推导
值得说明的是关于能量平衡方程的版本是不近统一的，争议的交点在于是否有（1-c）这个因子，本文采用的是比较普遍的带有（1-c）因子的能量平衡方程形式。
M
a
n
=
M
s
⋅
(
c
o
t
h
(
H
e
a
)
−
a
H
e
)
(
1
)
H
e
=
H
+
α
M
(
2
)
M
=
M
r
e
v
+
M
i
r
r
(
3
)
M
r
e
v
=
c
(
M
a
n
−
M
i
r
r
)
(
4
)
由
(
3
)
(
4
)
得：
d
M
i
r
r
=
(
d
M
−
c
d
M
a
n
)
(
1
−
c
)
(
5
)
能量平衡公式：
μ
0
∫
M
d
H
e
=
μ
0
∫
M
a
n
d
H
e
−
μ
0
k
δ
（
1
−
c
）
∫
(
d
M
i
r
r
d
H
e
)
d
H
e
(
6
)
将
(
5
）代入（
6
）式，再用（
2
）式换掉
H
e
得到（
7
）
:
M
=
M
a
n
−
δ
k
[
d
M
−
c
d
M
a
n
1
−
c
d
H
+
α
d
M
]
（
7
）
由（
7
）式解出
M
对
H
的积分：
d
M
d
H
=
(
1
−
c
)
(
M
a
n
−
M
)
+
c
δ
k
d
M
a
n
d
H
δ
k
−
α
(
1
−
c
)
(
M
a
n
−
M
)
(
8
)
式（
8
）即为
J
−
A
的正模型表达式。对于逆
J
−
A
模型的推导有些许不同：在能量平衡公式（
6
）的基础上
,
用
H
e
=
B
μ
0
−
(
α
−
1
)
M
换掉（
7
）式中的
H
e
：
M
=
M
a
n
−
δ
k
[
d
M
−
c
d
M
a
n
1
−
c
d
H
e
]
(
9
)
导出：
δ
k
1
−
c
(
d
M
d
H
e
−
c
d
M
a
n
d
H
e
)
=
M
a
n
−
M
换出
d
B
:
δ
k
1
−
c
(
d
M
d
B
d
H
e
d
B
−
c
d
M
a
n
d
H
e
)
=
M
a
n
−
M
(
9
−
1
)
d
H
e
d
B
=
1
μ
0
+
(
α
−
1
)
d
M
d
B
(
10
)
由（
9
−
1
）和（
10
）联立求得：
d
M
s
a
t
d
B
=
δ
M
(
M
a
n
−
M
s
a
t
)
+
c
k
δ
d
M
a
n
d
H
e
μ
0
[
(
1
−
α
)
(
δ
M
(
M
a
n
−
M
s
a
t
)
+
c
k
δ
d
M
a
n
d
H
e
)
+
k
δ
]
式中，
δ
M
=
{
1
,
sign
(
M
a
n
−
M
)
⋅
sign
(
d
H
/
d
t
)
≥
0
0
,
sign
(
M
a
n
−
M
)
⋅
sign
(
d
H
/
d
t
)
<
0
δ
取值
d
H
/
d
t
>
0
δ
=
1
δ
=
−
1
M_{an}=M_{s}\cdot (coth(\frac{H_e}{a})-{\frac{a}{H_e}}) \quad\qquad(1) \\ \quad\quad\quad\quad H_e=H+\alpha M \quad \quad \quad\quad \quad\quad (2)\\ \quad\quad M=M_{rev}+M_{irr} \quad\quad \quad\quad \quad\quad (3)\\ \quad\quad M_{rev}=c(M_{an}-M_{irr}) \quad\quad\quad \quad\quad(4)\\ 由(3)(4)得：dM_{irr}=\frac{(dM-cdM_{an})}{(1-c)} (5) \\ 能量平衡公式：\mu_0\int MdH_e=\mu_0\int M_{an}dH_e-\mu_0k\delta（1-c）\int(\frac{dM_{irr}}{dH_e})dH_e (6) \\ 将(5）代入（6）式，再用（2）式换掉He得到（7）:\\ M = M_{an}-\delta k[\frac{\frac{dM-cdM_{an}}{1-c}}{dH+\alpha dM}] （7）\\ \\ 由（7）式解出M对H的积分：\\ \\ \frac{dM}{dH}=\frac{(1-c)(M_{an}-M)+c\delta k\frac{dM_{an}}{dH}}{\delta k-\alpha(1-c)(M_{an}-M)} (8)\\ 式（8）即为J-A的正模型表达式。 对于逆J-A模型的推导有些许不同： 在能量平衡公式（6）的基础上,用H_e=\frac{B}{\mu_0}-(\alpha-1)M换掉（7）式中的H_e：\\ M = M_{an}-\delta k[\frac{\frac{dM-cdM_{an}}{1-c}}{dH_e}] (9)\\ 导出：\frac{\delta k}{1-c}(\frac{dM}{dH_e}-c\frac{dM_{an}}{dH_e})=M_{an}-M\\ 换出dB :\\ \frac{\delta k}{1-c}(\frac{\frac{dM}{dB}}{\frac{dH_e}{dB}}-c\frac{dM_{an}}{dH_e})=M_{an}-M (9-1)\\ \frac{dH_e}{dB}=\frac{1}{\mu_0}+(\alpha-1)\frac{dM}{dB} (10)\\ 由（9-1）和（10）联立求得：\\ \frac{\mathrm{d} M_{\mathrm{sat}}}{\mathrm{d} B}=\frac{\delta_{\mathrm{M}}\left(M_{\mathrm{an}}-M_{\mathrm{sat}}\right)+c k \delta \frac{\mathrm{d} M_{\mathrm{an}}}{\mathrm{d} H_{\mathrm{e}}}}{\mu_0\left[(1-\alpha)\left(\delta_{\mathrm{M}}\left(M_{\mathrm{an}}-M_{\mathrm{sat}}\right)+c k \delta \frac{\mathrm{d} M_{\mathrm{an}}}{\mathrm{d} H_{\mathrm{e}}}\right)+k \delta\right]} \\式中， \delta_{\mathrm{M}}=\left\{\begin{array}{l} 1, \operatorname{sign}\left(M_{\mathrm{an}}-M\right) \cdot \operatorname{sign}(\mathrm{d} H / \mathrm{d} t) \geq 0 \\ 0, \operatorname{sign}\left(M_{\mathrm{an}}-M\right) \cdot \operatorname{sign}(\mathrm{d} H / \mathrm{d} t)<0 \end{array}\right. δ 取值dH/dt>0 δ=1 δ=-1
Man=Ms⋅(coth(aHe)−Hea)(1)He=H+αM(2)M=Mrev+Mirr(3)Mrev=c(Man−Mirr)(4)由(3)(4)得：dMirr=(1−c)(dM−cdMan)(5)能量平衡公式：μ0∫MdHe=μ0∫MandHe−μ0kδ（1−c）∫(dHedMirr)dHe(6)将(5）代入（6）式，再用（2）式换掉He得到（7）:M=Man−δk[dH+αdM1−cdM−cdMan]（7）由（7）式解出M对H的积分：dHdM=δk−α(1−c)(Man−M)(1−c)(Man−M)+cδkdHdMan(8)式（8）即为J−A的正模型表达式。对于逆J−A模型的推导有些许不同：在能量平衡公式（6）的基础上,用He=μ0B−(α−1)M换掉（7）式中的He：M=Man−δk[dHe1−cdM−cdMan](9)导出：1−cδk(dHedM−cdHedMan)=Man−M换出dB:1−cδk(dBdHedBdM−cdHedMan)=Man−M(9−1)dBdHe=μ01+(α−1)dBdM(10)由（9−1）和（10）联立求得：dBdMsat=μ0[(1−α)(δM(Man−Msat)+ckδdHedMan)+kδ]δM(Man−Msat)+ckδdHedMan式中，δM={1,sign(Man−M)⋅sign(dH/dt)≥00,sign(Man−M)⋅sign(dH/dt)<0δ取值dH/dt>0δ=1δ=−1
三、静态 J-A模型程序编写
静态J-A模型本质是一阶常微分方程，可以用matlab自带的ode45()、ode23()、或者自己编写龙格-库塔、前向欧拉方法对其进行求解。但是J-A模型微分方程中有5个J-A模型参数（a,k,c,alpha,Ms）将其确定才能对其求解，对于参数的确定方法普遍采用智能优化算法，以实验测得的（B-H）数据为基准，让模型求解的（B-H）与实验测得（B-H）的偏差最小，该偏差一般以平均相对误差来估计，并且以平均相对误差为智能优化算法的目标函数。
在示例程序中，J- A模型参数（a,k,c,alpha,Ms）先假设已知，我们设定J-A模型参数如下：
a=1.152609e+00; k=2.005133e+00; c=4.683743e-01; alpha=2.113600e-06; Ms=7.193042e+05;
其中B 则为试验数据的B序列，这很重要，因为模型要想和数据拟合得好，就要求在相同的B （或者H 点） 通过通过模型来求解得到H（或者B）。辨识的时候也一样！
定义逆静态J- A模型求解函数dMdB：
function [H,B] = dMdB(a,k,c,alpha,Ms,B,M0)
H=zeros(size(B));
M=zeros(size(B));
miu0=4*pi*1e-7;
M(1)=M0;
H(1)=B(1)/miu0-M(1);
for i=2:length(B)
dB=B(i)-B(i-1);
He=B(i-1)/miu0+(alpha-1)*M(i-1);
Malpha=Mah_iso(a,Ms,He);
dM1 = (Malpha-M(i-1));
delta=sign(dB);
if sign(dB)>0
dM1(dM1<0)=0;
end
if sign(dB)<0
dM1(dM1>0)=0;
end
dM2=c*delta*k.*dMah_iso(a,Ms,He);
dM3=miu0.*((1-alpha).*(dM1+dM2)+k*delta);
dMdB=(dM1+dM2)./dM3;
M(i)=dB*dMdB+M(i-1);
H(i)=B(i-1)/miu0-M(i-1)
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function result = Mah_iso(a,Ms,He)
result=Ms.*(coth(He./a)-(a./He)); %无磁滞磁化强度Man
end
function result = dMah_iso(a,Ms,He) %无磁滞磁化强度Man对He求导
result=(Mah_iso(a,Ms,He+1e-6)-Mah_iso(a,Ms,He-1e-6))./2e-6; % 用导数的增量式来求导，而不是导数公式！！！！
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
调用逆静态J-A模型函数dMdB：
clc;clear all;close all;
[data]=xlsread("D:\BaiduSyncdisk\paper\1\程序\ZT动态JA模型\100.xlsx"); %这里修改成对应的测试数据路径
H_test=data(:,1);B_test=data(:,2);
miu0=4*pi*1e-7;
a=1.152609e+00; k=2.005133e+00; c=4.683743e-01; alpha=2.113600e-06; Ms=7.193042e+05; M0=B_test(1)/miu0-H_test(1);
[Hmodel,Bmodel]=dMdB(a,k,c,alpha,Ms,B_test,M0);
figure(1)
hold on
plot(H_test,B_test,"g-","LineWidth",2);
plot(Hmodel,Bmodel,"b-","LineWidth",2);
hold off
%绘图设置
xlabel('\itH/\rm(A/m)','fontsize',10);ylabel('\itB/\rmT','fontsize',10);
set(gca,'FontName','Times');
set(gca,'FontSize',10);
set(gca,'FontWeight','bold');
set(gca,'FontName','Times');
% 网格
grid on;
set(gca, 'GridLineStyle', '--'); % 设置为虚线
set(gca, 'GridAlpha', 1); % 设置透明度，注意参数的范围是[0,1]
%图例
legend('boxoff');
lg1=legend('Measured loops','Simulated loops');
set(lg1,'FontSize',10,'FontName','Times','FontWeight','bold');
set(lg1,'Location','northwest');
%设置输出的图的大小
set(gcf,'PaperUnits','centimeters')
set(gcf,'PaperSize',[28,11.4])
set(gcf,'PaperPositionMode','manual')
set(gcf,'PaperPosition',[0,0,28,11.4]);
set(gcf,'Renderer','painters');
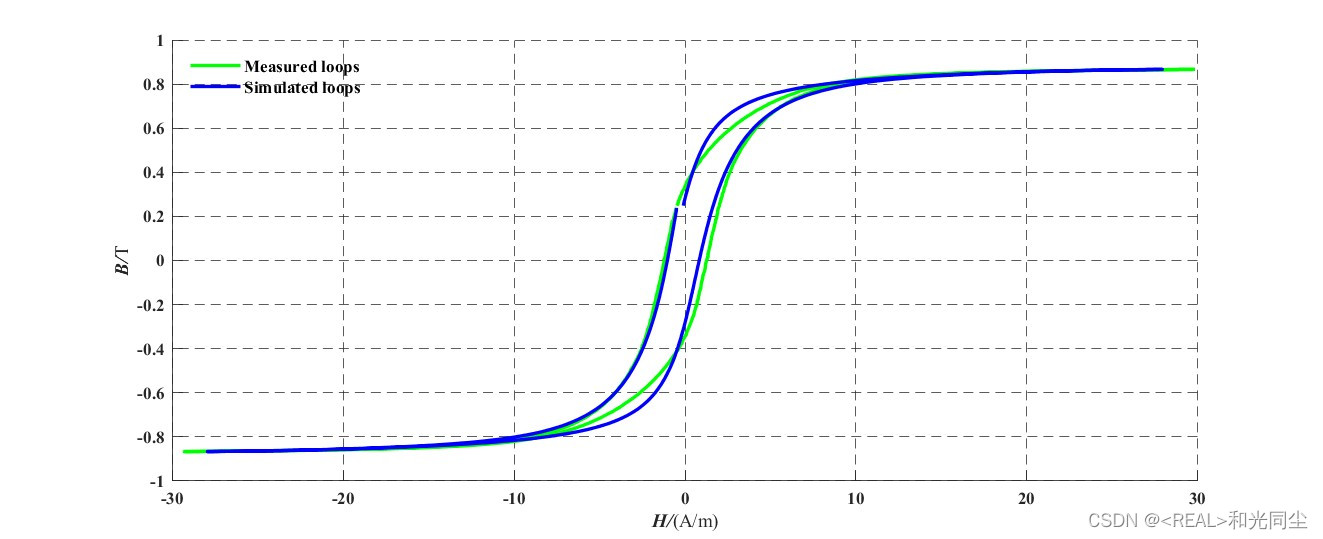
J-A模型求解结果及试验数据结果展示：
四、模型参数的辨识
磁滞模型的参数获取方式除了公式法之外，一般都是基于智能优化算法获取的。该方法是基于拟合的思想，以实测和计算的磁滞回线误差最小为目标，通过智能优化算法辨识得到参数。传统的粒子群（PSO）遗传算法（GA）等都可以应用。本文以PSO算法为例编写辨识程序。程序中的matlab文件同上文。
clear;clc
close all
%% 加载数据
%-------------------------%%%%%%%%%%%%%%%-%%%%%%%%%%%%%%%%----------0.5T------%%%%%%%%%%%%%%%%%%----------------%%%%%%%%%
data=xlsread("D:\BaiduSyncdisk\paper\1\程序\data\100.xlsx");
%--------------------%%%%%%%%%%%%----------------%%%%%%%%%%%%%%%%%-----------------%%%%%%%%%%%%%%%%%------------%
u0=4*pi*10^-7;
Breal=data(:,2);
Hreal=data(:,1);
N=5;
for i=1:N
Breal=smooth(Breal);
Hreal=smooth(Hreal);
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
a=1.061675e+00; k=1.993707e+00; c=4.278606e-01; alpha=2.099955e-06; Ms=7.163959e+05;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
gbest=[a k c alpha Ms];
%% 多次循环
CycleNumber = 5; % 按需增加
for z=1:CycleNumber
%% 预设参数
n = 100; %粒子数量
d = 5; %变量个数
c1 = 2;
c2 = 2;
w = 0.9;
K = 200; %迭代次数
%% 分布粒子
v = zeros(n,d);
x = zeros(n,d);
x(1:n-1,1) = a*1.5*rand(n-1,1);
x(1:n-1,2) = k*2*rand(n-1,1);
x(1:n-1,3) = abs(c)*2*rand(n-1,1);
x(1:n-1,4) = alpha*2*rand(n-1,1);
x(1:n-1,5) = Ms*2*rand(n-1,1);
x(n,:)=gbest;
%% 计算适应度
fit = zeros(n,1);
for j = 1:n
M0=Breal(1)/(4*pi*1e-7)-Hreal(1);
fit(j) = JAFitnessFun(x(j,:),Breal,M0,Hreal);
end
pbest = x;
ind = find(min(fit) == fit);
gbest = x(ind,:);
%% 更新速度与位置
for i = 1:K
% 更新速度与位置
for m = 1:n
v(m,:) = w*v(m,:) + c1*rand*(pbest(m,:) - x(m,:)) + c2*rand*(gbest - x(m,:));
x(m,:) = x(m,:) + v(m,:);
% 重新计算适应度
fit(m) = JAFitnessFun(x(m,:),Breal,M0,Hreal);
if fit(m) < JAFitnessFun(pbest(m,:),Breal,M0,Hreal)
pbest(m,:) = x(m,:);
end
if JAFitnessFun(pbest(m,:),Breal,M0,Hreal) < JAFitnessFun(gbest,Breal,M0,Hreal)
gbest = pbest(m,:);
end
end
fitnessbest((z-1)*K+i) = JAFitnessFun(gbest,Breal,M0,Hreal);
end
[Hmodel,Bmodel] =dMdB(gbest(1),gbest(2),gbest(3),gbest(4),gbest(5),Breal,M0);
a=gbest(1); k=gbest(2); c=gbest(3); alpha=gbest(4); Ms=gbest(5);
clc;fprintf("当前已完成%f个周期",z);
end
fprintf('参数辨识值: \na=%e; k=%e; c=%e; alpha=%e; Ms=%e; \n\n',gbest);
figure(1)
hold on
plot(Hreal,Breal,'LineWidth',2,'Color',[255/255,128/255,0/255],"LineStyle","-");
plot(Hmodel,Bmodel,"lineWidth",2,"Color",[64/255,105/255,224/255],"LineStyle","-.");
hold off;
%坐标轴
box on;
%修改边框
xlabel('\itH/\rm(A/m)','fontsize',10);ylabel('\itB/\rmT','fontsize',10);
% set(gca,'FontWeight','bold');
set(gca,'FontName','Times');
% xlim([-15,15]);ylim([-0.6,0.6]);
% xticks(-15:5:15);yticks(-0.5:0.2:0.5);
set(gca,'FontSize',10);
set(gca,'FontWeight','bold');
set(gca,'FontName','Times');
% 网格
grid on;
set(gca, 'GridLineStyle', '--'); % 设置为虚线
set(gca, 'GridAlpha', 1); % 设置透明度，注意参数的范围是[0,1]
%图例
legend('boxoff');
lg1=legend('Simulated loops','Measured loops');
set(lg1,'FontSize',10,'FontName','Times','FontWeight','bold');
set(lg1,'Location','northwest');
%设置输出的图的大小
set(gcf,'PaperUnits','centimeters')
set(gcf,'PaperSize',[28,11.4])
set(gcf,'PaperPositionMode','manual')
set(gcf,'PaperPosition',[0,0,28,11.4]);
set(gcf,'Renderer','painters');
%计算适应度函数
function y = JAFitnessFun(x,B,M0,Hreal)
[Hmodel,~] = dMdB(x(1),x(2),x(3),x(4),x(5),B,M0); %根据辨识出的五个参数值计算磁感应强度B
y = sqrt(sum((Hreal-Hmodel).^2)./size(B,1)); %适应度函数
end
结果如下：
a=1.153081e+00; k=1.931425e+00; c=4.259512e-01; alpha=2.131973e-06; Ms=7.193425e+05;
试验结果和辨识结果如下：
微信：“TavianZhu”，欢迎交流！
扫一扫
3175
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
