AVL树的基本操作是几种旋转方法。
觉得这篇文章讲解的很好很全面,就拿来分享了。
一、引言
由于普通二叉查找树可能出现有极不平衡的情况,使时间复杂度最坏,于是有学者提出限制二叉查找树各子树的分布,使树形状平衡,保证较好的查找复杂度。其中最著名平衡树之一即为AVL树。二、AVL树的定义
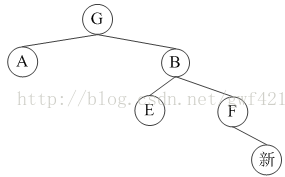
官方的定义可以参见其它网上资料。在这里我用大白话解释,话粗理不粗。有一对有兄弟A和B,他们的共同父亲是G。AVL树绝对不允许这种情况出现:
这对兄弟其中一人没有孩子,另外一人却当上了爷爷。
三、AVL树的八种违例情况
网上有很多总结,说四种情况。但是经常把同类型的几种情况列举出来,另外的几种却忽略不说。导致初学AVL树的朋友都糊里糊涂的。就列侯捷老师的《STL源码剖析》都是讲得不明不白。
本文干脆把八种情况都列举出来,一次性讲解。
还记得上文的定义吗?所谓AVL树违例,本来一个家庭好好的(合理AVL树),却因为这个家庭新添了一丁(插入一节点),使得兄弟A和B,一人没有孩子,另一个却当上了爷爷。
如果当上爷爷的是A,没孩子的是B,有如下四种情况,
(1)
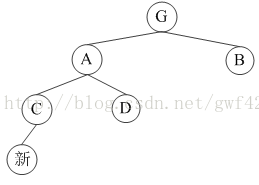
(2)
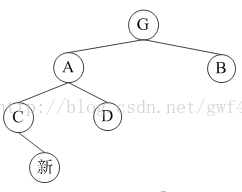
(3)
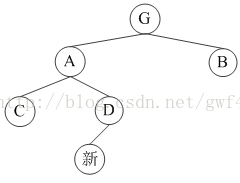
(4)
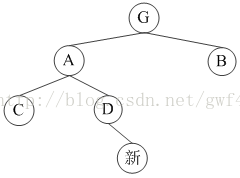
反之,如果当上爷爷是B,无孩子是A,有如下四种情况,
(5)

(6)
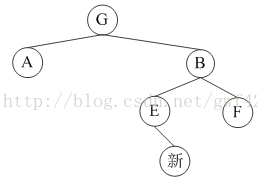
(7)
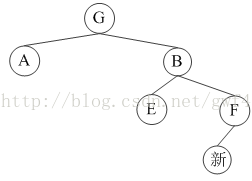
(8)
加起来共八种情况。
侯捷老师把情况(1、2)合称左左。他的视点是从根节点出发的,情况(1、2)统称为“插入操作发生在根节点的左节点的左子树”。同理,情况(3、4)合称左右。情况(5、6)合称右左。情况(7、8)合称右右。
另一位博主(http://www.cnblogs.com/huangxincheng/archive/2012/07/22/2603956.html)却把情况1称左左、情况2称左右、情况7称右左、情况8称右右。中间的情况3、4、5、6全都丢失了,完全不合理。
其实wiki的画法也十分清晰明了(http://zh.wikipedia.org/wiki/AVL%E6%A0%91)
另一位博主(http://blog.163.com/di_yang@yeah/blog/static/86118492201231724250191/)的说法比较特别,虽然语言有所偏颇,但是有其道理。
四、AVL树的旋转
因为出现了违例,那么必须对这个家庭采取一些措施,使其变回合法的AVL树。
我们在这里结合侯捷老师、wiki和博主(http://blog.163.com/di_yang@yeah/blog/static/86118492201231724250191/)的说法来解释怎么进行AVL树旋转。
1、什么是合理的旋转策略
首先要明确一条原则,旋转是改变树的局部排列。由于局部的排列改变,牵一发而动全身,整棵AVL树也有可能被调整。我们要注意避免不收敛情况,即:这边调整好,却引发那边违例,待那边处理好,又出现新的违例。有一条原则,从G开始这个小家庭的对上接口可以改变(实际上必面改变),但是对下接口不变。什么意思?以情况(3)为例,
对上的接口就是该子树的根,即G节点。对下接口是叶节点,包括C、B和新加入的节点。合理的旋转策略是,旋转后子树的三个叶节点仍然是C、新、B。
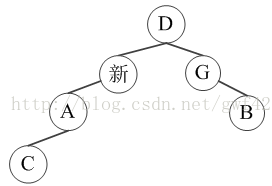
例如,如果情况(3)旋转成下图这个样子,
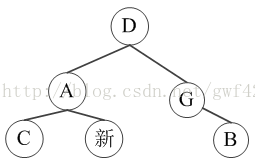
按AVL树要求来说是合法的(没有出现两个子树高度差超过1的情况)。但是要想到,这个子树有可能在一棵很大的AVL树的中部。它对下面的接口变了,变成只有C和B。那么就会引起下面的子树调整。下面的子树调整又引起旁边和更下面的子树调整,没完没了了。合理的旋转后,应该对下接口仍为C、新、B,即
所以,我们要保证,下接口不变,变动的只有上接口(根节点)。然后本子树的根节点看作是上层子树的新插入节点。如此递归,最终只要改变至总根节点(大部分情况下不必去到总根节点,具体终止条件在源码中讲解)
2、单旋转
2.1、单次右旋转
违例情况(1、2),使用单次左旋转。因为两种情况新节点分别插在位置1和2处,我们统一画出来,但请记住1、2同时有新节点是不可能的,下同。
左旋转的算法很简单,只有三步。对于一个输入节点X,只有该节点X,和该节点的左儿子Y参与到变换,
INPUT: knot X
1. Y = X.left
2. X.left = Y.right
3. Y.right = X
在图中,把整棵违规子树的根节点G输入到左旋算法中,即有
INPUT: knot G
1. A = G.left
2. G.left = A.right (即是D)
3. A.right = G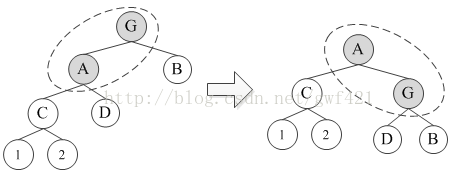
2.2、单次左旋转
违例情况(7、8),使用单次右旋转。同理为了减少示意思,我们统一画出7、8,实际上不可能同时有新节点。
右旋转同样只有三步。只有输入节点X和该节点的右儿子Y参与变换。
INPUT: knot X
1. Y = X.right
2. X.right = Y.left
3. Y.left = XINPUT: knot G
1. B = G.right
2. G.right = B.left (即是E)
3. B.left = G
3、双旋转
3.1、先左旋再右旋
违例情况(3、4),使用先右旋、再左旋转,两次旋转。3、4位新节点同时画出只为方便示意。
先右旋,输入A
INPUT: knot A
1. D = A.right
2. A.right = D.left (即是3)
3. D.left = A
图:
再左旋,输入G
INPUT: knot G
1. D = G.left
2. G.left = D.right (即是4)
3. D.right = G
3.2、先右旋再左旋
违例情况(5、6),使用先左旋、再右旋转,两次旋转。5、6位新节点同时画出只为方便示意。
先左旋,输入B
INPUT: B
1. E = B.left
2. B.left = E.right (即是6)
3. E.right = B
再右旋,输入G
INPUT: G
1. E = G.right
2. G.right = E.left (即是5)
3. E.left = G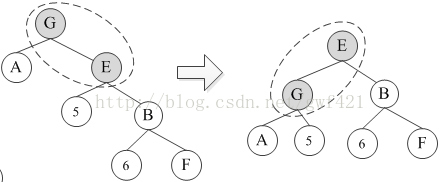























 580
580

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








