动态规划基础

w1711246

已于 2023-08-31 20:22:32 修改

阅读量332

点赞数

分类专栏： leetcode一刷文章标签：动态规划算法 leetcode

于 2023-02-03 23:16:09 首次发布

本文链接：https://blog.csdn.net/w1711246/article/details/128867481

版权

leetcode一刷专栏收录该内容

16 篇文章 0 订阅

订阅专栏

文章介绍了动态规划的基础，包括五步曲模型，如确定dp数组、递推公式、初始化、遍历顺序和调试方法。通过具体题目如509斐波那契数、70爬楼梯、746使用最小花费爬楼梯等，展示了动态规划的应用，强调了边界条件和优化空间复杂度的重要性。

摘要由CSDN通过智能技术生成

理论

1、动态规划五步曲

确定dp数组（dp table）以及下标的含义
确定递推公式
dp数组如何初始化
确定遍历顺序
举例推导dp数组

2、动态规划应该如何debug
最好方式就是把dp数组打印出来，看看究竟是不是按照自己思路推导的

动态规划

题目

509 斐波那契数

class Solution:
    def fib(self, n: int) -> int:
        
        #  - 确定dp数组（dp table）以及下标的含义 
        #dp = []  # 下标即n  数值为F(n)
        # - 确定递推公式 
        # dp(n) = dp(n-1) + dp(n-2)
        # - dp数组如何初始化 
        # dp[0]=0
        # dp[1]=1
        # - 确定遍历顺序  由小到大
        # - 举例推导dp数组
        # dp = [0 1 1 2 3 5 8]

        '''
        if n <=1:
            return n
        dp = [None]*(n+1)
        dp[0]=0
        dp[1]=1
        for i in range(2,n+1):
            dp[i] = dp[i-1]+dp[i-2]
        return dp[-1]
        '''
        # 简化 只要存前两个数即可
        if n <=1:
            return n
        a = 0
        b = 1
        for i in range(2,n+1):
            c = a+b
            a = b
            b = c
        return b

70 爬楼梯

爬n层楼梯等于
第一次爬一层的方法数爬（n-1）的方法数+第一次爬两层的方法数爬（n-2）的方法数

class Solution:
    def climbStairs(self, n: int) -> int:
        if n<=2:
            return n
        a = 1
        b = 2
        for _ in range(n-2):
            c = a+b
            a,b = b, c
        return b

注：使用递归会超时

746 使用最小花费爬楼梯

确定dp数组（dp table）以及下标的含义
dp[i]：到达第i个位置的花费
确定递推公式
到达第i个位置的花费等于到达第i-2个位置的花费+cost2与到达第i-1个位置的花费+cost1的较小值
dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
dp数组如何初始化
初始化dp[0],dp[1] 由题意的到这两个位置不用花费均为0
确定遍历顺序
从小到大
举例推导dp数组

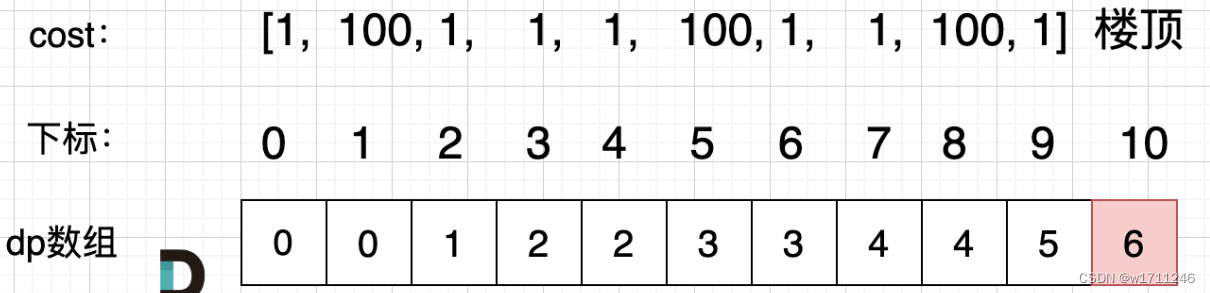
注意：楼顶是第n+1个位置

class Solution:
    def minCostClimbingStairs(self, cost: List[int]) -> int:
        n = len(cost)
        dp = [None]*(n+1)
        dp[0] = 0  # 到达第0/1个位置不需要支付
        dp[1] = 0
        for i in range(2, n+1):
            dp[i] = min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])
        return dp[-1]
        # 减小内存开销：只保存前两个dp

62 不同路径

确定dp数组（dp table）以及下标的含义
dp[i][j]：到达第[i][j]个位置的路径数
确定递推公式
到达第[i][j]个位置的路径数等于其上位置的路径数+左位置的路径数
dp[i][j]= dp[i-1][j]+dp[i][j-1]
dp数组如何初始化
初始化dp[0][j],dp[i][0] 最左侧和最上层的位置的路径数都为1，也避免了i-1，j-1超过索引范围
确定遍历顺序
等于左节点加上节点路径，所以从左至右，从上至下遍历
举例推导dp数组

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        dp = [[1]*n for _ in range(m)]
        for i in range(1,m):
            for j in range(1,n):
                dp[i][j] = dp[i][j-1]+dp[i-1][j]
        return dp[m-1][n-1]

63 不同路径 II

在上题的基础上随机放入一个障碍物
重点：边界条件；障碍物出的路径数为0
len返回的是数组最外围的大小

class Solution:
    def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
        # 障碍物所在的位置的路径数为0
        m = len(obstacleGrid)  # len返回的是数组最外围的大小
        n = len(obstacleGrid[0])
        dp = [[0]*n for _ in range(m)]  # 不要预设  可能障碍物就处于边界
        for i in range(m):
            for j in range(n):
                if obstacleGrid[i][j]==0:  # 非障碍物                   
                    if i == 0 and j==0:
                        dp[i][j]= 1
                    elif i == 0:  # 第1行非首元素
                        dp[i][j] = dp[i][j-1]
                    elif j==0:
                        dp[i][j]=dp[i-1][j]
                    else:
                        dp[i][j]=dp[i-1][j]+dp[i][j-1]
        return dp[m-1][n-1]

64. 最小路径和

class Solution:
    def minPathSum(self, grid: List[List[int]]) -> int:
        # dp[i][j]：i.j处得到的最小路径

        m = len(grid)
        n = len(grid[0])
        dp = [[100]*n for _ in range(m)]
        dp[0][0] = grid[0][0]
        for j in range(1,n):
            dp[0][j] = dp[0][j-1] + grid[0][j]
        for i in range(1,m):
            dp[i][0] = dp[i-1][0] + grid[i][0]

        for i in range(1, m):
            for j in range(1, n):
                dp[i][j] = min(dp[i-1][j], dp[i][j-1]) +grid[i][j]
        return dp[-1][-1]

遍历顺序可交换

343 整数拆分

假设对正整数 i 拆分出的第一个正整数是 j（1 <= j < i），则有以下两种方案：

将 i 拆分成 j 和 i−j 的和，且 i−j 不再拆分成多个正整数，此时的乘积是 j * (i-j)
将 i 拆分成 j 和 i−j 的和，且 i−j 继续拆分成多个正整数，此时的乘积是 j * dp[i-j]

class Solution:
    def integerBreak(self, n: int) -> int:
        dp = [0]*(n+1)
        dp[2]=1
        for i in range(3,n+1):
            for j in range(1,i//2+1):  # 遍历一半即可 越接近越大
                dp[i] = max(j*(i-j),j*dp[i-j],dp[i])  # 不断更新dp[i] 始终存放最大值
        return dp[-1]

时间复杂度：O(n^2)
空间复杂度：O(n)

for j in range(1,i//2+1)：
因为拆分一个数n 使之乘积最大，那么一定是拆分成m个近似相同的子数相乘才是最大的。

例如 6 拆成 3 * 3， 10 拆成 3 * 3 * 4。 100的话也是拆成m个近似数组的子数相乘才是最大的。

只不过我们不知道m究竟是多少而已，但可以明确的是m一定大于等于2，既然m大于等于2，也就是最差也应该是拆成两个相同的可能是最大值。

96 不同的二叉搜索树

添加链接描述
dp[3] = dp[2]×dp[0] + dp[1]×dp[1] + dp[0]×dp[2]
分析：以三个节点为例，三节点的二叉搜索树等于：
以1为根节点，左子树0，右子树2（数字指节点数）
以2为根节点，左子树1，右子树1
以3为根节点，左子树2，右子树0
规律：若计算i个节点能构成的二叉搜索树数量，其等于以不同的j(1<=j<=i)作为根节点的二叉搜索树的和，左子树结点数为j-1，右子树结点数为i-j
注：上述定义中会出现j-1等于0的情况，由以上分析知，将其设置为1

class Solution:
    def numTrees(self, n: int) -> int:
        dp = [0]*(n+1)
        dp[0] = 1
        dp[1] = 1
        for i in range(2,n+1):
            for j in range(1,i+1):
                dp[i] = dp[i]+dp[j-1]*dp[i-j]
        return dp[-1]