论文复现《Deep Landscape Forecasting for Real-time Bidding Advertising》

最新推荐文章于 2024-09-25 15:58:18 发布

w55100

最新推荐文章于 2024-09-25 15:58:18 发布

阅读量3k

点赞数 7

分类专栏： pytorch

本文链接：https://blog.csdn.net/w55100/article/details/90401199

版权

pytorch 专栏收录该内容

27 篇文章

订阅专栏

本文为笔记。

原论文：《Deep Landscape Forecasting for Real-time Bidding Advertising》
Authors: Kan Ren, Jiarui Qin, Lei Zheng, Zhengyu Yang, Weinan Zhang, Yong Yu
https://arxiv.org/abs/1905.03028
KDD2019

背景介绍

这篇文章讲的是广告竞价里，怎么预测整个价格空间。
现在的二次竞价制度，第一名的出价 = 第二名的出价+一个很小的bonus
也就是说，第二名的价格就是胜者面对的“市场价格”，超过这个市场价格，就能获胜。

举个不严谨的例子，假设第二名出价10元，第三第四第五名就更小了，不需要考虑。
你要考虑的只有竞争对手里面出价最高的那一个。
那么，只要你出价高于10元，哪怕你出价是999999999999999999元，系统也会判定你胜出，然后你只需要支付10.01元。
这就是二次竞价制度。
以上为个人听完2019腾讯广告算法live的理解。

看完论文有一大堆疑问。
怀疑原文是不是笔误了，有多处符号跟我想的不太一样。
所以我按自己的理解再推一次。

一、理论部分

1.1 市场价格z

先定义market price (市场价格) 为变量z，显然z>0
于是z的概率密度函数可以定义为
$p (z), z > 0$
为了简便起见，概率密度函数 Probability Density Function下文简称 P.D.F. （笑出声）。

于是可以推导出以出价b获胜与竞价失败的概率。

$\doteq Pr(z<b) = \int_{0}^{b} p(z)dz \qquad$
$\doteq Pr(z \ge b) = 1-\int_{0}^{b} p(z)dz \qquad$
(公式4)

1.2 离散价格模型

整个市场价格空间中，分布着一系列的价格 $b 1, b 2, b 3, . . ., b l$ ，为了使模型更合理，我们显然可以在某一个角度，把这些价格全部看做整数，即 $b_{l}-b_{l-1} =1$ 。

个人补充

为什么可以看做整数？因为人类社会存在精度precision概念。
哪怕你的cpc广告出价是1块3毛每千次点击，这个1块3毛也可以转成1.03（元），转成103（分）。那么下一个出价就是104(分)。
在max精度的视角下，总可以得到一系列离散的整数。

我们人为地约定 $b_{0} = 0$

然后，定义离散价格区间（internal）
$V_{l} = \lbrack b_{l},b_{l+1})$

这里原文是左开右闭，我认为应该是左闭右开才符合逻辑。
因为z = b的时候，当前b就成了第二名的出价，显然b无法获胜。
你们也可以自己推一遍

在这里插入图片描述
那么现在我们就有了新的win和lose概率公式

给定出价bl：
$w(b_{l}) = Pr(z<b_{l}) = \sum_{j=0}^{l-1} (z \in V_{j}) \qquad$
$s(b_{l}) = Pr(z>=b_{l}) = \sum_{j=l}^{\infty} (z \in V_{j}) \qquad$

我们再定义，z恰好落在 $V_{l}$ 区间内的概率为
$p_{l} \doteq Pr(Z \in V_{l}) = W(b_{l+1}) - W(b_{l}) \\ = [1-S(b_{l+1}) ] - [1-S(b_{l})] \\ =S(b_{l}) - S(b_{l+1})$
(公式5)

于是我们的模型转化为了
给定一组数据 ${(x,b,z)}$ ，求概率密度函数 $p (z)$ 。
细一点说就是，对 $\ th \ samle$ ，求 $P.D.F. of z^i，p(z^i | x^i)$ 。

其中作为label的z对win case是可见的，对lose case是不可知的，被设为null。
因为广告竞价失败的广告主，只知道自己这个价格不行，不知道哪个价格可以。

可是我们知道，p(z)不好直接求，需要对其进行进一步的转化。

我们构造辅助变量 $h_{l}$ ，约定其现实意义为，已知出价 $b_{l-1}$ 失败，那么出价 $b_{l}$ 恰好获胜的概率。

$h_{l} = Pr(z \in V_{l-1} | z \ge b_{l-1}) \\ = \frac {Pr(z \in V_{l-1})}{Pr(z \ge b_{l-1})} = \frac {p_{l-1}}{S_{b_{l-1}}}$
(公式6)

在这里插入图片描述
备注

原文定义的 $h_{l} = \frac {p_{l}}{ s_{b_{l-1}}}$
可是若按照 $V_{l}$ 的空间划分和 $h_{l}$ 的现实意义来看，分子的下标应该是 $l - 1$ 而非 $l$
是我理解错了还是怎么回事？
而且从后面的代码来看，这个 $h_{l}$ 不像是winning probability，倒像是lose probability?

在这里插入图片描述

1.3 价格空间预测

完成了上面的准备公式，下面可以正式将问题的数学建模，转换成神经网络可以操作的形式。

作者引入RNN模型，因为一堆参考文献123456789都表现的挺好，而且我们的公式中可以看出来，离散价格区间有明显的序列特征。用n-1去推n正是RNN擅长的事情。

将RNN网络看成一个大的函数 $f_{\theta}$ ，则可以将公式（6）进一步写成。

$h_{l}^i = Pr( z \in V_{l-1} | z \ge b_{l-1},x^i;\theta) \\ =f_{\theta} (x^i,b_{l} | r_{l-1})$
公式（7）

第二步的下标为什么加一了？

解释：我们的 $h_{l}$ 的现实意义是，已知出价 $b_{l-1}$ 失败，那么出价 $b_{l}$ 恰好获胜的概率。
对应到 $f_{\theta}$ 中， $r_{l-1}$ 就是上一个RNN Cell传过来的 " $b_{l-1}$ 失败了"的信息， $f_{\theta}$ 要去计算出价 $b_{l}$ 恰好获胜的概率。
所以写成了 $f_{\theta} (x^i,b_{l} | r_{l-1})$ 。

本文选用的RNN Cell是标准的LSTM Unit。

重点
由公式(4),(6),(7)可以推出以出价 $b_{l}$ 失败的概率
$S(b_{l} | x^i;\theta) = Pr( z \ge b_{l} | x^i;\theta) \\ = Pr( z \notin V_{1}, z \notin V_{2},...,z \notin V_{l-1} | x^i ;\theta) \\ = Pr(z \notin V_{1} |x^i ;\theta)*Pr(z \notin V_{2},...,z \notin V_{l-1} | z \notin V_{1},x^i ;\theta ) \\ =Pr(z \notin V_{1} | x^i ;\theta)*Pr(z \notin V_{2} | z \notin V_{1},x^i;\theta)*Pr(z \notin V_{3},...,z \notin V_{l-1} | z \notin V_{1},z \notin V_{2},x^i ;\theta ) \\ = Pr(z \notin V_{1} | x^i ;\theta)*Pr(z \notin V_{2} | z \notin V_{1},x^i;\theta)*Pr(z \notin V_{3} | z \notin V_{1},z \notin V_{2}, x^i ;\theta)*...\\ *Pr(z \notin V_{l-1} | z \notin V_{1},z \notin V_{2}, ...,z \notin V_{l-2},x^i ;\theta) \\ =Pr(z \notin V_{1} | x^i ;\theta) *Pr(z \notin V_{2} | z \ge b_{2},x^i ;\theta)*Pr(z \notin V_{3} | z \ge b_{3},x^i;\theta)*...*Pr(z \notin V_{l-1} | z \ge b_{l-1},x^i;\theta)\\ =\prod_{k=1}^{l-1} Pr(z \notin V_{k} | z \ge b_{k},x^i;\theta) \\ =\prod_{k=1}^{l-1} [ 1 - Pr (z \in V_{k} | z \ge b_{k},x^i;\theta) ]\\ \xlongequal{公式(6),(7)} \prod_{k=1}^{l-1} [1-h_{k+1}^i] \\ \xlongequal{} \prod_{0<k<l}^{} [1-h_{k+1}^i]$
$W(b_{l} | x^i;\theta) = 1 - S(b_{l} | x^i;\theta) \\ = 1- \prod_{0<k<l}^{} [1-h_{k+1}^i]$ 公式(8)

对公式(8)的备注

在现实生活中，市场价格不可能为0，所以我们知道 $z\ge b_{1}$ 是必然事件，
$Pr(z\ge b_{1})=1$
所以公式中的推导中的第一项可以写成
$\notin V_{1} | x^i ;\theta) = Pr(z \notin V_{1} | z\ge b_{1}, x^i ;\theta)$
所以可以合并为k=1时，连乘号里的项。

再放一次图防止忘记。
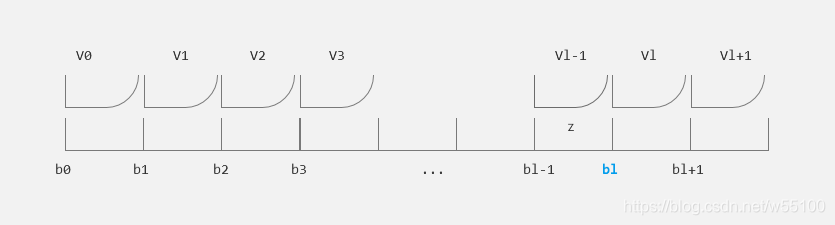
在这里插入图片描述

现在有了公式(8)，它的价值在于，现在我们可以用RNN 网络的输出值 $h_{l}$ 来计算测试集的某条记录的win和lose概率了。相当于是一个连接器bridge。

我们再由公式(5),(6)可知，对第i个样本而言， $z^i$ 刚好落在区间 $V_{l-1}$ 的概率:
$p_{l-1}^i = Pr(z^i \in V_{l-1} | x^i;\theta) = h_{l}^i \cdot S_{b_{l-1}}^i \\ =h_{l}^i \prod_{0<k<l-1}^{} [1-h_{k+1}^i] \\ =h_{l}^i \prod_{1<k<l}^{} [1-h_{k}^i]$
公式(9)

备注

然而看完代码你会发现这条公式并没有被用到。
能用公式(5)算 $p_{l}$ ，为什么要用公式(9)。
可是既然如此，你为什么要推一次公式(9)呢…
凑字数？

1.4 损失函数与目标方程

完成了RNN网络的准备部分，现在我们可以引入loss function了。

原文分为2个视角进行定义。

吐槽，C.D.F.的概念第一次出现在第5页，却在第9页才写备注，还得猜半天这什么意思

1.4.1 先从P.D.F. 概率密度函数的角度看。

我们使用negative log-likehood (负对数似然)作为loss。
显然给定一个win样本，我们就知道了市场价格为 $\in V_{l}$ 。
我们就希望网络预测的 $\in V_{l} | x^i;\theta) \to 1$

把m个样本的 $\in V_{l} | x^i;\theta)$ 全部乘起来，得到
$\prod_{ x^i,z^i \in \Bbb{D}_{win}} Pr(z^i \in V_{l} | x^i;\theta) \\ = -log \prod_{ x^i,z^i \in \Bbb{D}_{win}} p_{l}^i \\ \xlongequal{公式(9)} -log \prod_{ x^i,z^i \in \Bbb{D}_{win}} \{ h_{l+1}^i \prod_{1<k<l+1}^{} (1-h_{k}^i) \} \\ = - \sum_{x^i,z^i \in \Bbb{D}_{win}} \{ log h_{l+1}^i + log \prod_{1<k<l+1} (1-h_{k}^i) \} \\ = - \sum_{x^i,z^i \in \Bbb{D}_{win}} \{ log h_{l+1}^i + \sum_{0<k<l} log(1-h_{k}^i) \}$
公式(10)

于是我们可以用RNN的输出 $h_{k}^i$ 来计算L1损失，其中k表示第k个价格区间。

备注

醉了，我在看代码的时候还纳闷，怎么没出现L1啊？
原来这个作者在后面还介绍了一种metric方法，叫average negative log probability (ANLP) 。
再定睛一看，这个ANLP不就是测试集上的L1损失吗！！！
代码里也清清楚楚的写了总损失 $c o m c o s t = a l p h a * L 2 + b e t a * a n l p$
在代码里面L1也直接被作者命名为anlp了，更加证明是两者同一个东西。
那你为什么要给同一个东西标志2个名字，还煞有介事的专门开一节介绍ANLP，凑字数吗？直接说 this equals to L1 introduced above不可以吗？
不搞多重命名，就是对我们最大的善意了！

1.4.2 视角2 从C.D.F的角度看

先解释C.D.F. (corresponding winning probability)，简而言之就是获胜概率。
整篇文章的公式只有2类。
第1类就是P.D.F.的，以z为主体，问 $\in V_{l}$ 的概率。
第2类就是C.D.F的，以bid为主体，问以出价 $b_{l}$ 获胜、失败的概率。
举例就去看1.3部分，里面的公式(8)属于C.D.F获胜概率，公式(9)属于P.D.F.落在某个价格区间的概率。

显然，对win case而言，我们希望
$Pr(z^i <b^i_{l} | x^i;\theta) \to 1$
对lose case而言，我们希望
$Pr(z^i \ge b_{l}^i | x^i;\theta) \to 1$

于是可以定义:
$L_{win} = -log \prod_{x^i,b^i \in \Bbb{D}_{win}} Pr(z^i < b_{l}^i | x^i;\theta) \\ = - log \prod_{x^i,b^i \in \Bbb{D}_{win}} W(b_{l} | x^i;\theta) \\ = - \sum _{x^i,b^i \in \Bbb{D}_{win}} log[ 1- \prod_{0<k<l}^{} (1-h_{k+1}^i)]$

再定义：
$L_{los} = -log \prod_{x^i,b^i \in \Bbb{D}_{lose}} Pr(z^i \ge b_{l}^i | x^i;\theta) \\ = - log \prod_{x^i,b^i \in \Bbb{D}_{win}} S(b_{l} | x^i;\theta) \\ = - \sum _{x^i,b^i \in \Bbb{D}_{win}} log[ \prod_{0<k<l}^{} (1-h_{k+1}^i)] \\ = - \sum_{x^i,b^i \in \Bbb{D}_{win}} \sum_{0<k<l} log(1-h_{k+1}^i)$
公式(11)

备注

原文这里不知道是不是写错了，我觉得不应该有等号。

为了把 $L_{win}$ 与 $L_{lose}$ 结合起来，我们引入一个记号数 $w$ ，它的作用相当于二分类的指示器（indicator ）。

对第i个样本：
$w^i = \begin{cases} 1, &\text{if } b^i>z^i \\ 0, &\text{otherwise } b^i \le z^i \end{cases}$
于是可以推出
$L_{2} = L_{win}+L_{lose} \\ = -log\prod _{x^i,b^i \in \Bbb{D}_{win}} Pr(z^i < b_{l}^i | x^i;\theta) -log \prod_{x^i,b^i \in \Bbb{D}_{lose}} Pr(z^i \ge b_{l}^i | x^i;\theta) \\ =-log\prod _{x^i,b^i \in \Bbb{D}} Pr(z^i < b_{l}^i | x^i;\theta)^{w^i} \cdot Pr(z^i \ge b_{l}^i | x^i;\theta)^{1-w^i} \\ =- \sum_{x^i,b^i \in \Bbb{D}} \{ w^i \cdot log W(b^i|x^i;\theta) + (1-w^i)\cdot log[1-W(b^i|x^i;\theta)] \}$
公式(14)

于是总的目标方程：
$\arg \min_{\theta} \alpha L_{1} + (1- \alpha ) L_{2}$

备注

然而在作者的github代码里，代价函数是这样写的
总损失 $\\ = 1.2 *(L2loss+ 0.001*L2norm) + 0.2*anlp$
跟论文里的有一定差别。
在前面L1损失那节说过了，这个anlp在作者眼里相当于前面的L1损失项（实际上并不完全一致）。
而这个L2损失项我也标明了，不仅仅是L2损失，还加了一个L2正则项。

理论部分，完毕。
事实证明，理论可以漂亮，实践还得tricky。

补充
L2就是某种意义上的交叉熵。

L1其实是一个商业领域的要求了。
回到广告业务上，我们不仅仅希望知道当前的bid，能否赢得这次auction。
我们还希望以最小的价格获胜。
那么我们希望预测出的关于z的概率密度，能在 $\in V_{l-1}$ 这个价格区间内，无限接近于1，这样才能使损失项L1接近于0。
而 $\in V_{l-1}) \to1$ 可以让我恰好用价格 $b_{l}$ 来获胜，这是最完美的答卷。

若在 $\in V_{l-1})$ 概率离1越远，我们就越有可能多付钱才能获胜，这便是L1损失的实际含义。

二.代码部分

原作者开源地址:
https://github.com/rk2900/DLF

原文这里为什么要加个点？

从/python/BASE_MODEL.py开始

batchsize=64
n_features =16	
MAX_SEQ_LEN = 330
embd_dim = 32	#embedding
state_size = 128 #rnn cell
mid_feature_size = 30 #中间dense层

#先把所有特征全部embd一下，然后hstack在一起，组成(64,16*32)
#input = (batchsize,n_features*embd_dim)

#dense层，把(16*32)降维到(30)，relu作为激活
middle_layer = tf.layers.dense(input, self.MIDDLE_FEATURE_SIZE, tf.nn.relu)  # hidden layer

#现在我们得到一个dense_x =(batchsize,mid_feature_size)
#对其中第i个sample，x=(mid_feature_size)
#对应我们公式里的xi
#由于是RNN，对l个区间，需要重复l次输入，于是需要复制l次xi。
#为了平衡不同的样本的b，对应的l值不同，统一复制max_seq_len次。
x = tf.reshape(tf.tile(x, [self.MAX_SEQ_LEN]), [self.MAX_SEQ_LEN, self.MIDDLE_FEATURE_SIZE])
#再合并成input_x = (batchsize,max_seq_len,mid_feature_size)


#定义LSTM网络
rnn_cell = tf.contrib.rnn.BasicLSTMCell(num_units=self.STATE_SIZE)

outputs, (h_c, h_n) = tf.nn.dynamic_rnn(
                rnn_cell,                   # cell you have chosen
                input_x,                    # input
                initial_state=None,         # the initial hidden state
                dtype=tf.float32,           # must given if set initial_state = None
                time_major=False,           # False: (batch, time step, input); True: (time step, batch, input)
                sequence_length=self.tf_rnn_len
            )
            
#lstm的输出output = (batchsize,max_seq_len,state_size)
#需要变形处理，用一个全连接层降到1维，然后转成概率hl
#
new_output = tf.reshape(outputs, [self.MAX_SEQ_LEN * BATCH_SIZE, self.STATE_SIZE])
logits = tf.matmul(new_output, W) + b
#logits = (batchsize*max_seq_len,1)
preds = tf.transpose(tf.nn.sigmoid(logits, name="preds"), name="preds")[0]
#preds = (1,batchsize*max_seq_len)[0] = (batchsize*max_seq_len)


#survival_rate 同 (batchsize*max_seq_len)
survival_rate = preds

#batch_rnn_survival_rate = (batchsize,max_seq_len)
#对应max_seq_len个hl,l in range(max_seq_len)
batch_rnn_survival_rate = tf.reshape(survival_rate, [BATCH_SIZE, self.MAX_SEQ_LEN])


#再经过2次tf.concat()
map_parameter = tf.concat()
#map_parameter 
# =batchsize*cat[(batchsize,MAX_SEQ_LEN ,bid_len,market_price] 
# =(batchsize,MAX_SEQ_LEN+1+1) ，这就是论文里的(x,b,z)

#对前面输处进行连乘 h0*h1*......*hl, l = bid_len
#h0*h1*......*hl, l = market_len
def reduce_mul(x):
    bid_len = tf.cast(x[self.MAX_SEQ_LEN], dtype=tf.int32)
    market_len = tf.cast(x[self.MAX_SEQ_LEN + 1], dtype=tf.int32)
    survival_rate_last_one = tf.reduce_prod(x[0:bid_len])
    anlp_rate_last_one = tf.reduce_prod(x[0:market_len + 1])
    anlp_rate_last_two = tf.reduce_prod(x[0:market_len])
    ret = tf.stack([survival_rate_last_one, anlp_rate_last_one, anlp_rate_last_two])
    return ret

#经过这步rate_result = (batchsize,3)
rate_result = tf.map_fn(reduce_mul, elems=map_parameter ,name="rate_result")

#log(anlp_rate_last_two - anlp_rate_last_one+1e-20)
#猜测加上1e-20是防止两个的生存概率都降到0，log报错。
#这步要结合公式(5)来看
#得到(1,batchsize)，表示每个sample的pz(z|x)
log_minus = tf.log(tf.add(tf.transpose(rate_result)[2] - tf.transpose(rate_result)[1], 1e-20))#todo debug

#取平均值，再乘(-1)，计算anlp (average negative log probability)
#结合公式(10)来看
anlp_node = -tf.reduce_sum(log_minus) / self.BATCH_SIZE #todo load name
anlp_node = tf.add(sanlp_node, 0, name="anlp_node")

#在bid所属价格区间的生存概率,(1,batchsize)
final_survival_rate = tf.transpose(rate_result)[0]

#1-s=w，就是死亡概率,(1,batchsize)
final_dead_rate = tf.subtract(tf.constant(1.0, dtype=tf.float32), self.final_survival_rate)

#predict = (batchsize,2)
predict = tf.transpose(tf.stack([final_survival_rate, final_dead_rate]), name="predict")

#tf_y = (batchsize,2) 标识0,1，计算交叉熵
cross_entropy = -tf.reduce_sum(self.tf_y*tf.log(tf.clip_by_value(self.predict,1e-10,1.0)))

#计算所有训练变量的L2损失
tvars = tf.trainable_variables()
lossL2 = tf.add_n([ tf.nn.l2_loss(v) for v in tvars ]) * 0.001

#加在一起
cost = tf.add(cross_entropy, lossL2, name = "cost")  / self.BATCH_SIZE

optimizer = tf.train.AdamOptimizer(learning_rate=self.LR, beta2=0.99)#.minimize(cost)
optimizer_anlp = tf.train.AdamOptimizer(learning_rate=self.ANLP_LR, beta2=0.99)#.minimize(cost)

#梯度修剪
grads, _ = tf.clip_by_global_norm(tf.gradients(self.cost, tvars),
                                          self.GRAD_CLIP, #self.GRAD_CLIP=5.0
                                          )
self.train_op = optimizer.apply_gradients(zip(grads, tvars), name="train_op")

#anlp梯度修剪
anlp_grads, _ = tf.clip_by_global_norm(tf.gradients(self.anlp_node, tvars),
                                          self.GRAD_CLIP,
                                          )
self.anlp_train_op = optimizer_anlp.apply_gradients(zip(anlp_grads, tvars), name="anlp_train_op")

#这才是我们的总Loss = 0.25*cost(L2) + 0.75*anlp_cost(L1)
self.com_cost = tf.add(alpha * self.cost, beta * self.anlp_node)


#同样做修剪
com_grads, _ = tf.clip_by_global_norm(tf.gradients(self.com_cost, tvars),
                                          self.GRAD_CLIP,
                                          )
self.com_train_op = optimizer.apply_gradients(zip(com_grads, tvars), name="train_op")

tf.add_to_collection('train_op', self.train_op)
tf.add_to_collection('anlp_train_op', self.anlp_train_op)
tf.add_to_collection('com_train_op', self.com_train_op)

#这里的逻辑是tf_y提供win和lose case的，显然我们人为在对应索引位置上的生存/死亡概率应该大于另一方。
#举例第i行，是lose case，那么tf_y[i,0]=1,tf_y[i,1]=0
#predict[i,0]应该趋向于1，大于predict[i,1]
correct_pred = tf.equal(tf.argmax(predict, 1), tf.argmax(tf_y, 1))
self.accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32), name="accuracy")


#后面train部分
#要记住，对win case 可以同时计算L1+L2，所以用self.com_cost对应的self.com_train_op
#对lose case，只能算L2，没有L1，所以用sel.cost对应的self.train_op

简单自学了一下生存分析。
原论文里面说，他们也是采用了不预先估计参数分布的KM分析法。

可是不同之处在于，KM是传入一组样本，估计同一个时间序列。
而价格空间预测，是把【时间序列】替换成了【价格序列】。
把【结束事件】即【死亡】替换成了【竞价成功】。
把【生存概率函数S(t)】替换成了【失败概率函数S(b)】。
而且，对 $i_{th} sample$ 而言，组内样本数为1，而不是KM或者传统医学分析里面的传入m个样本。

但是这样，就又要求RNN的输出是conditional suvival_rate,即出价 $b_{l}$ 的【条件失败概率】。
可原文的前面又把 $h_{l}$ 定义为 ‘just’ winning probability。
为什么是winning…？应该是losing啊!

我认为，前面的定义都可以改一下。
实际上RNN输出的不是前面定义的 $h_{l}$ ，而是 $1-h_{l}$ 。（划重点啊！！！）

本模型中，在 $b_{l}$ 的 失败概率S(b) 就是所谓的 生存概率。
根据 $S(b_{l})$ 的计算式，公式(8)，我们知道在 $b_{l}$ 的生存概率，或者说失败概率S(b)，可以用RNN网络的前 $l$ 个输出值 $1-h_{1})*(1-h_{2})*...*(1-h_{l})$ 计算得到。
在这里插入图片描述

有了 $S(b_{l})$ ，1减一下，就得到在 $b_{l}$ 的获胜概率，或者说死亡概率 $W(b_{l})$ 。、
然后就能算交叉熵L2了。

至于L1，或者说作者眼中的anlp。
先说anlp，
简单而言就是，对某个win case来说，模型预测的 $z^i$ 落在区间 $V_{l}$ 上的概率的负对数值， $-logPr(z^i \in V_{l} | x ^i)$ 。
其中 $V_{l}$ 是这个win case标注好的市场价格z的所属区间。
然后对群体样本求个均值即可。
在这里插入图片描述

乍一看anlp的定义，和我们推导的L1很像。
但L1公式里面，根本没有均值这个概念！

$\prod_{ x^i,z^i \in \Bbb{D}_{win}} Pr(z^i \in V_{l} | x^i;\theta) \\ = - \sum_{ x^i,z^i \in \Bbb{D}_{win}} log Pr(z^i \in V_{l} | x^i;\theta)$

这很可能又是一个笔误。

更新0524

完成了在pytorch上的复现。
果然我理解的没错，RNN的输出并非论文里的 $h_{l}$ ，而是生存分析里的条件生存概率，在本论文中即指 $1-h_{l}$ ，条件竞价失败概率。

数据集采用的是作者附赠在开源代码里的的toy dataset ‘2259’。

toy dataset 是原话！

真的很toy啊，总共才8k多数据。

超参数全部抄作者的。
Adagrad, lr=0.002。
大概30个epoch开始，lose case的corss_entropy损失就0.01~0.0之间徘徊了。
对应的概率值为
$e x p (- 0.03) = 0.9704$
$e x p (- 0.01) = 0.9900$
结果上来说挺不错了。