感想
问题的形式化
神经网络的学习过程可以形式化为最小化损失函数问题,该损失函数一般是由训练误差和正则项组成。误差项会衡量神经网络拟合数据集的好坏,也就是拟合数据产生的误差。正则项主要是通过给特征权重增加惩罚项而控制神经网络的有效复杂度,这样可以有效地控制过拟合问题。
训练损失函数取决于神经网络中的自适应参数(偏置项和权重),我们很容易地将神经网络的权重重组合成一个n维权重向量w,而训练损失就是以这些权重为变量的函数。下图描述了损失函数f(W)。
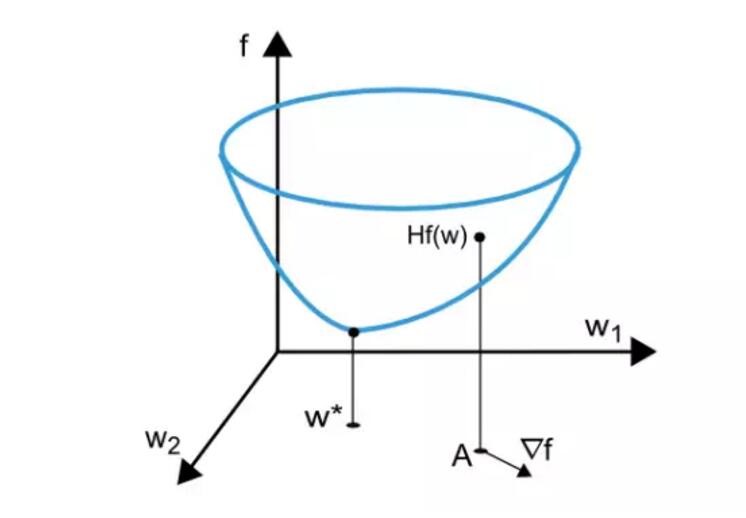
如上图所示,w*是训练损失函数的极小值点,在任意点A,损失函数能分别对权重求一阶偏导数和二阶偏导数。损失函数的一阶偏导可以使用梯度算符来表示,其中一个权重的损失函数梯度表示如下:


单变量函数优化(One-dimensional optimization)
虽然损失函数是由多变量决定的(权重的数量通常十分巨大),但首先理解单变量函数的优化方法是十分重要的。并且实际上单变量优化方法经常应用到神经网络的训练过程中,超参数的调整就可以使用单变量优化法。
在实际模型中,许多训练算法都是首先计算出训练方向d,然后确定在此训练方向上最小化训练损失f(η)的学习速率η。下图就展示了单变量函数f(η)的优化过程,该优化可求得最优学习率η*。
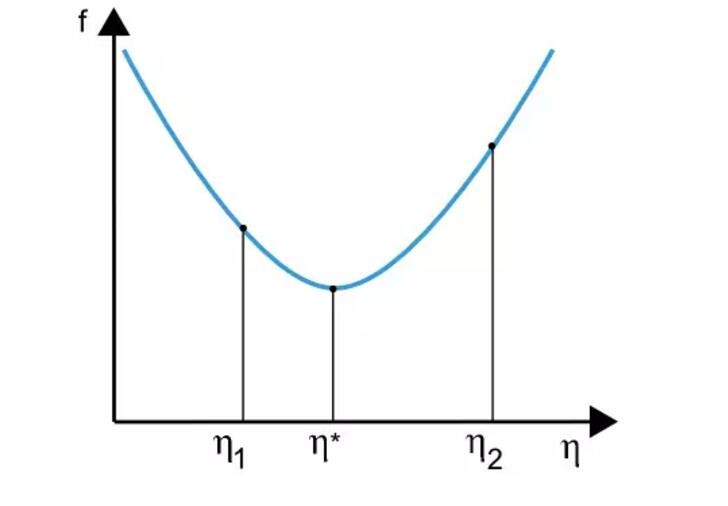
点η1和点η2定义了包含单变量函数f(η)最优点η*的子区间。
在该案例中,单变量优化法在给定单变量函数的情况下搜寻函数极小值。其中广泛应用的搜寻算法有黄金分割点(golden selection)和Brent法。两者都是在减少极小值所在的子区间,直到子区间中两个端点间的距离小于定义的可容忍误差。
多变量函数优化(Multidimensional optimization)
神经网络的学习过程可以形式化为求将损失函数f最小化的参数向量w*,数学或实际都证明如果如果神经网络的损失函数达到了极小值,那么梯度也必定为0向量。通常情况下,损失函数为参数的非线性函数,所以找到一个封闭的训练算法(closed training algorithms)求最优解是不可能的。相反,我们考虑通过一系列迭代步在参数空间内搜寻最优解。在每一步迭代中,我们可以通过调整神经网络的参数降低损失函数的值。通过这种方式,一般我们我们会由初始参数向量开始(通常为随机初始化)训练神经网络。然后,算法会更新生成一组新参数,训练损失函数也会在每一次算法迭代中使用更新的参数进行函数值的降低。两步迭代之间的训练损失减少又称之为训练损失衰减率(loss decrement)。最后,当训练过程满足特定条件或停止标准时,训练算法就会停止迭代,而这个时候的参数也就是最优的参数。
梯度下降法
梯度下降,又称为最速下降法,是一种非常简单和直观的训练算法。该算法从梯度向量中获取优化信息,因此其为一阶算法(通过一阶偏导求最优权重)。梯度下降法是用平面去拟合当前的局部曲面。
如果我们指定 f(wi)= fi、ᐁf(wi)= gi,梯度下降法为:
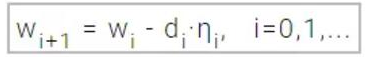
其中η是学习率。该学习率的值可以设定为一个常量也可以沿着方向使用单变量优化法求得。通常学习速率的最优值可以在连续迭代步(successive step)上通过线最小化(line minimization)获得。然而,现在还是有很多机器学习模型仅仅只使用固定的学习速率。
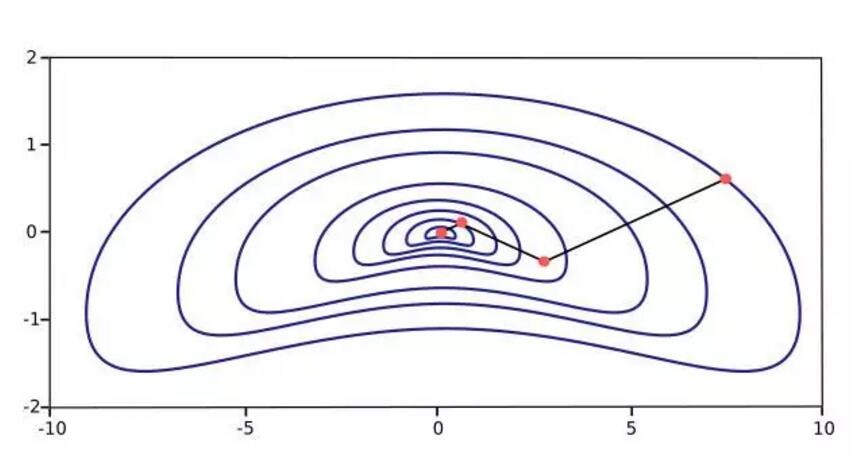
梯度下降算法也有一些缺点,首先就是其迭代方向会呈现一种锯齿现象,其并不能朝着极小值点径直优化,所以迭代的次数也就多,收敛的速度也就慢。当它的函数梯度图又窄又长时(变量没有归一化,值处于不同的量级),迭代所需要的步数就会更多了。最速下降法确实沿着最陡的梯度下降,损失函数减少得最迅速,但这并不代表梯度下降法或最速下降法会最快收敛(因为锯齿现象)。如下图
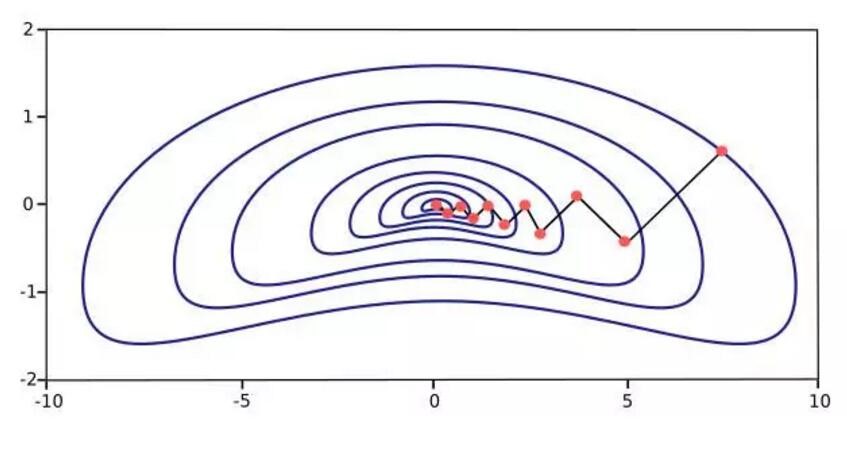
在训练大规模神经网络时,因为有上万的参数,所以梯度下降法是比较有效的。因为梯度下降算法储存的梯度算符向量规模为n,而海森矩阵储存的规模为n^2,同时梯度和海森矩阵的计算量也是天差地别。
牛顿法
牛顿法是二阶算法,因为该算法使用了海森矩阵(Hessian matrix)求权重的二阶偏导数。牛顿法的目标就是采用损失函数的二阶偏导数寻找更好的训练方向。
因此牛顿下降法是用二次曲面去拟合当前的局部曲面,现在采用如下表示:f(wi) = fi、ᐁf(wi) = gi 和 Hf(wi) = Hi。在w0点使用泰勒级数展开式二次逼近函数f.
H0为函数f在点w0的海森矩阵,对w求导,得到g,通过将g设定为0,我们就可以找到f(w)的最小值,也就得到了以下方程式。
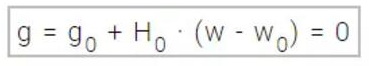
因此,从参数向量w0开始,牛顿法服从以下方式进行迭代:
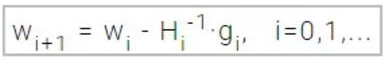
向量 Hi-1·gi也就是所说的牛顿下降步(Newton's step)。注意,参数的这些变化将朝着极大值而不是极小值逼近,出现这样的情况是因为海森矩阵非正定。
因此在不能保证矩阵正定的情况下,损失函数并不能保证在每一次迭代中都是减少的。为了防止上述问题,牛顿法的方程式通常可以修改为:
学习速率η同样可是设定为固定常数或通过单变量优化取值。向量d=Hi-1·gi现在就称为牛顿训练方向(Newton's training direction)。
使用牛顿法的训练过程状态图如下,系统首先通过获得牛顿训练方向,然后获得合适的学习速率来进行参数的更新优化。
下图的梯度图展示了牛顿法的性能,因为牛顿法是采用其损失函数的二阶偏导数寻找更好的训练下降方向,所以它相比梯度下降只要更少的迭代次数就能下降到损失函数
的最小值,因此收敛的速度也会大幅度地加快。
然而,牛顿法的困难之处在于其计算量,因为对于海森矩阵及其逆的精确求值在计算量方面是十分巨大的。
这里解释一下Hessian矩阵:形式如下
当f(x)为二次函数时,梯度以及Hessian矩阵很容易求得。二次函数可以写成下列形式:
其中 x为列向量,A 是 n 阶对称矩阵,b 是 n 维列向量, c 是常数。f(x) 梯度是 Ax+b, Hesse 矩阵等于 A。如果想要了解更多,读者就只能自行查阅资料了。
共轭梯度法(Conjugate gradient)
在共轭梯度训练算法中,因为是沿着共轭方向(conjugate directions)执行搜索的,所以通常该算法要比沿着梯度下降方向优化收敛得更迅速。共轭梯度法的训练方向
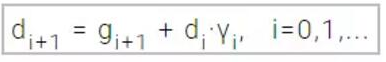
上式中,Y称之为共轭参数,并且有一些方法计算这个参数。两种常用的方法源自Fletcher、Reeves 和 Polak 、Ribiere。对于所有的共轭梯度算法,训练方向
周期性地重置为负梯度方向。参数通过下面的表达式得以更新和优化,通常学习速率η可使用单变量函数优化方法求得。
共轭梯度法的训练过程流程图如下表示,从图中我们可以看出来模型是通过第一次计算共轭梯度训练方向而优化参数的,然后再寻找适当的学习速率。
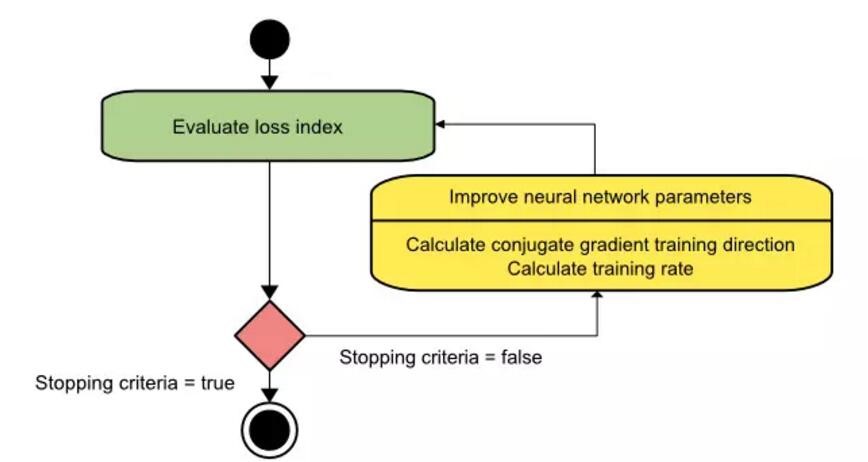
共轭梯度法已经证实其在神经网络中要比梯度下降法有效得多。并且由于共轭梯度法并没有要求使用海森矩阵,所以在大规模神经网络中其还可以做到很好的性能。
拟牛顿法(Quasi-Newton method)
因为需要很多的操作求解海森矩阵的值还有计算矩阵的逆,应用牛顿法的计算量是十分巨大的。因此有一种称之为拟牛顿法(quasi-Newton)或
变量矩阵法来解决这样的缺点。这些方法并不是直接计算海森矩阵然后求其矩阵的逆,拟牛顿法是在每次迭代的时候计算一个矩阵,其逼近海森矩阵的逆。
最重要的是,该逼近值只是使用损失函数的一阶偏导来计算。
海森矩阵由损失函数的二阶偏导组成,拟牛顿法背后的思想主要是仅使用损失函数的一阶偏导数,通过另一矩阵G逼近海森矩阵的逆。拟牛顿法的公式可以表示为:
学习速率η可以设定为固定常数,也可以通过单变量函数优化得到。其中矩阵G逼近海森矩阵的逆,且有不同的方式进行逼近。通常,最常用的两种方式是
Davidon–Fletcher–Powell formula (DFP) 和 the Broyden–Fletcher–Goldfarb–Shanno formula (BFGS)。
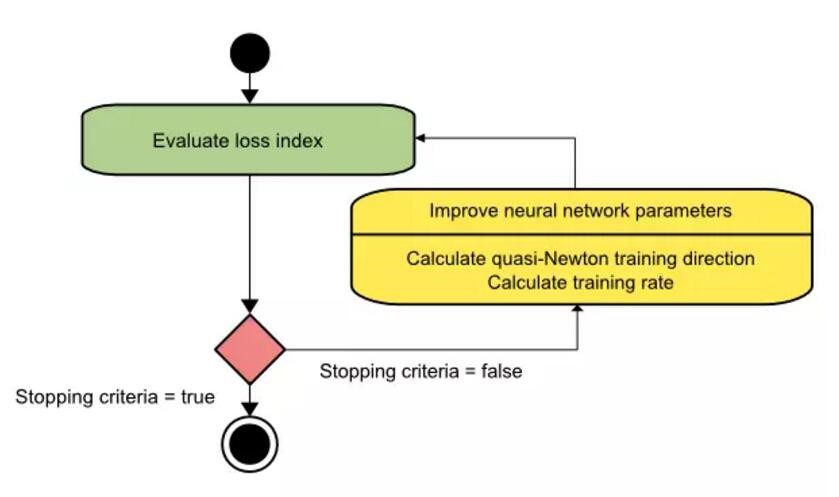
拟牛顿法的训练过程流程图如下所示,从图中我们可以看出来模型是通过第一次计算拟牛顿训练方向而优化参数的,然后再寻找适当的学习速率。
拟牛顿法适用于绝大多数案例中:它比梯度下降和共轭梯度法收敛更快,并且也不需要确切地计算海森矩阵及其逆矩阵。
Levenberg-Marquardt 算法,也称为衰减最小二乘法(damped least-squares method),该算法的损失函数采用平方误差和的形式。该算法的执行也不需要
计算具体的海森矩阵,它仅仅只是使用梯度向量和雅克比矩阵(Jacobian matrix)。
这里解释一下雅克比矩阵(Jacobian matrix):Jacobi 矩阵实际上是向量值函数的梯度矩阵,假设F:Rn→Rm 是一个从n维欧氏空间转换到m维欧氏空间的函数。
这个函数由m个实函数组成:
这些函数的偏导数(如果存在)可以组成一个m行n列的矩阵(m by n),这就是所谓的雅可比矩阵:
该算法的损失函数如下方程式所示为平方误差和的形式:
在上式中,m是数据集样本的数量。
我们可以定义损失函数的雅可比矩阵以误差对参数的偏导数为元素,公式如下:
其中m是数据集样本的数量,n是神经网络的参数向量。那么雅可比矩阵是m*n阶矩阵,损失函数的梯度向量就可以按如下计算出来:
E在这里是所有误差项的向量。
最终,我们可以利用一下表达式逼近海森矩阵:
其中λ为衰减因子,它确保了海森矩阵的证定性(positiveness),I是单位矩阵。下面的表达式定义了Levenberg-Marquardt 算法中参数的更新和优化过程:
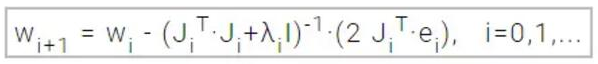
当衰减参数λ为0时,Levenberg-Marquardt 算法就是使用海塞矩阵逼近值的牛顿法。而当λ很大时,该算法就近似于采用很小学习速率的梯度下降法。如果进行迭代导致了
损失函数上升,衰减因子λ就会下降,从而Levenberg-Marquardt 算法更接近于牛顿法。该过程经常用于加速收敛到极小值点。
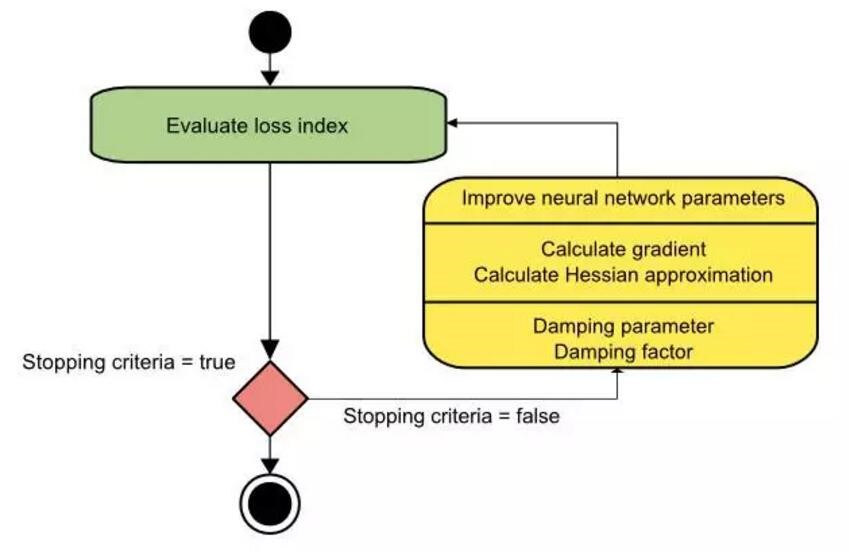
如图,第一步就是计算损失函数、梯度和海森矩阵逼近值,随后再在每次迭代降低损失中调整衰减参数。
Levenberg-Marquardt 算法是为平方误差和函数所定制的。这就让使用这种误差度量的神经网络训练地十分迅速。但是其缺点是:
1. 它不能用于平方根误差或交叉熵误差(cross entropy error)等函数。
2. 该算法与正则项不兼容。
3. 对于大型数据集或神经网络,雅可比矩阵变得十分巨大,因此也需要大量的内存。
在大型数据集或神经网络中并不推荐采用Levenberg-Marquardt 算法。
内存与收敛速度的比较
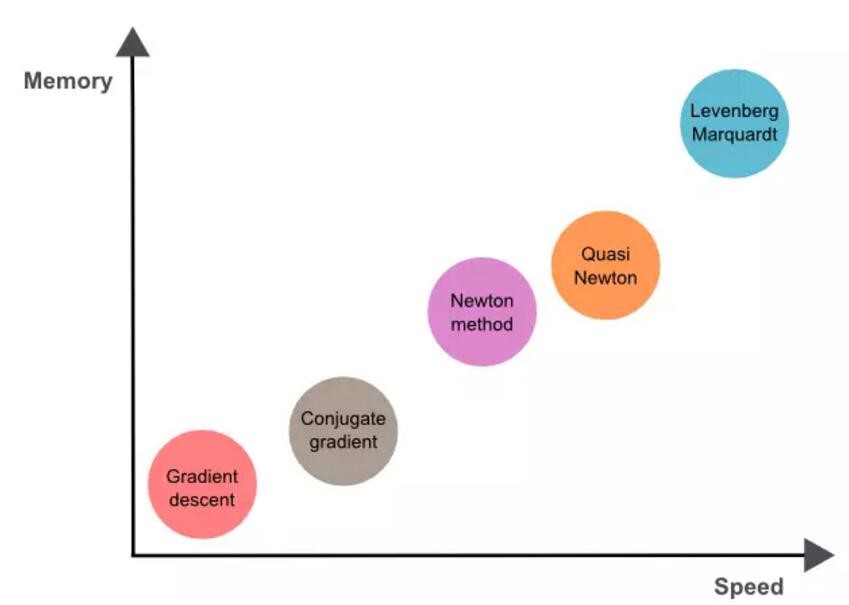
如图,收敛速度最慢的是梯度下降算法,但该算法同时也只要求最少内存。相反,Levenberg-Marquardt 算法可能是收敛速度最快的,但其同时也要求最多的内存。
比较折中的方法是拟牛顿法。
总而言之,如果我们的神经网络有数万参数,为了节约内存,我们可以使用梯度下降或共轭梯度法。如果我们需要训练多个神经网络,并且每个神经网络都只有数百参数
、数千样本,那么我们可以考虑 Levenberg-Marquardt 算法。而其余的情况,拟牛顿法都能很好地应对。
参考文献
[1]. 从梯度下降到拟牛顿法:详解训练神经网络的五大学习算法.
https://www.jiqizhixin.com/articles/2017-03-11-2





 本文深入浅出地介绍了梯度下降法、牛顿法、共轭梯度法等五种优化算法,探讨了它们在神经网络训练中的应用及优劣对比。
本文深入浅出地介绍了梯度下降法、牛顿法、共轭梯度法等五种优化算法,探讨了它们在神经网络训练中的应用及优劣对比。
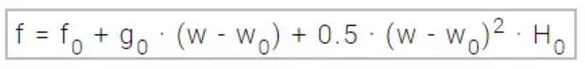



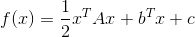
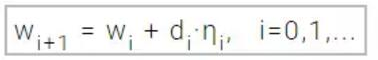
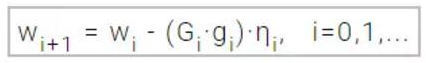

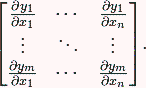
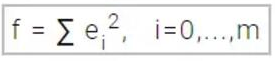
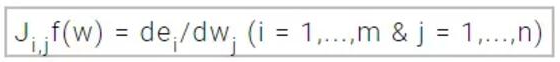
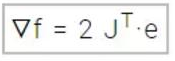


















 1168
1168

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










