题目链接:点击打开链接
题目大意:求矩阵A+A^2+A^3....+A^k
题目思路:一开始也没什么思路,但是看到一篇博客。。。
今天我们学习如何有效地求表达式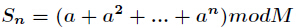
(1)当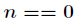
(2)当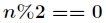
(3)当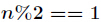
然后就照着撸就行了...
这里的关键就是提取的公因子,如果我们直接去计算的话那么显然是会超时的,那我们从式子入手会发现上述的提取方法,接下来会发现每一次的变化规则相同,其实就可以递归优化一下,也可以叫倍增,复杂度为log^2k*1600
ac代码:
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream>
#include<sstream>
#include<cmath>
#define LL long long
#define INF 0x3f3f3f3f
#define INFLL 0X3f3f3f3f3f3f3f
#define lson rt<<1
#define rson rt<<1|1
using namespace std;
int n,k;
struct mat
{
int a[45][45];
mat()
{
memset(a,0,sizeof(mat));
}
};
mat mutil(mat a,mat b)
{
mat ret;
for(int i = 0;i<n;i++){
for(int j = 0;j<n;j++){
for(int k = 0;k<n;k++){
ret.a[i][k] = (ret.a[i][k]%10+a.a[i][j]%10*b.a[j][k]%10)%10;
}
}
}
return ret;
}
mat add(mat a,mat b)
{
for(int i = 0;i<n;i++){
for(int j = 0;j<n;j++){
a.a[i][j] = (a.a[i][j]%10+b.a[i][j]%10)%10;
}
}
return a;
}
mat pow(mat a,int nn){
mat ret;
for(int i = 0;i<n;i++){
for(int j = 0;j<n;j++){
ret.a[i][j] = (i==j);
}
}
while(nn){
if(nn&1) ret = mutil(a,ret);
a = mutil(a,a);
nn >>=1;
}
return ret;
}
mat solve(mat A,int nn)
{
if(nn==1)
return A;
mat ret = solve(A,nn/2);
if(nn%2==1){
mat tmp = pow(A,nn/2+1);
ret = add(ret,mutil(ret,tmp));
ret = add(ret,tmp);
}
else{
mat tmp = pow(A,nn/2);
ret = add(ret,mutil(ret,tmp));
}
return ret;
}
int main()
{
while(~scanf("%d%d",&n,&k))
{
if(!n)
break;
mat ans;
for(int i = 0;i<n;i++){
for(int j = 0;j<n;j++){
scanf("%d",&ans.a[i][j]);
ans.a[i][j] %= 10;
}
}
ans = solve(ans,k);
for(int i = 0;i<n;i++){
for(int j = 0;j<n;j++){
printf("%d%c",ans.a[i][j]%10,j==n-1?'\n':' ');
}
}
puts("");
}
}







 该博客介绍了如何使用矩阵快速幂和二分优化方法解决UVA 11149问题,即求解矩阵A的幂次和。通过提取公因子并利用递归优化(倍增),将复杂度降低到log^2k*1600,从而避免超时。文章提供了关键思路和AC代码。
该博客介绍了如何使用矩阵快速幂和二分优化方法解决UVA 11149问题,即求解矩阵A的幂次和。通过提取公因子并利用递归优化(倍增),将复杂度降低到log^2k*1600,从而避免超时。文章提供了关键思路和AC代码。
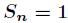
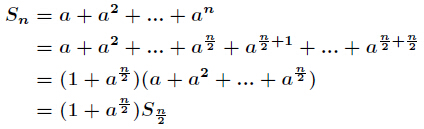
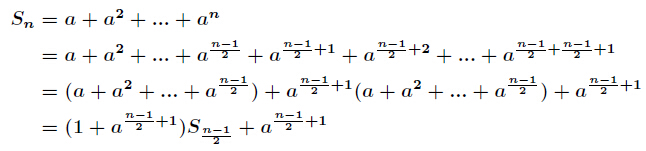














 530
530

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








