分布式之拜占庭问题

写在前面

拜占庭问题是对分布式系统中共识问题(所有节点对某一问题达成相同的看法)的一种情景化描述，其描述中有3位将军，3位将军围困一座城池，如下图：

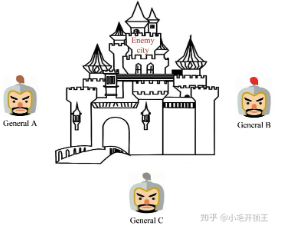
在决定是否进攻城池之前，3位将军需要协商进攻还是撤退，这个协商的过程通过信使传达消息来完成，每位将军在观察敌情之后做出进攻和撤退的决定，通过信使来将自己的决定传达给另外两位将军，如果进攻的话，必须至少2位将军同时进攻才能攻下城池，否则将会攻占城池失败。即3位将军需要对进攻城池还是撤退达成共识，如果3位将军都是忠诚的，则会一切正常，如下图：

此时三位将军得到指令如下(千万不要忘了自己的一票)：

将军A，进攻：撤退=2：1，最终进攻
将军B，进攻：撤退=2：1，最终进攻
将军C，进攻：撤退=2：1，最终进攻

最终三位将军同时进攻，攻入城池，大破敌军，但，3位将军可能有叛徒，其会发送错误消息给另外两位将军，最终造成可能只有一位将军进攻城池，导致失败的结果，如下图将军C是叛徒的场景：

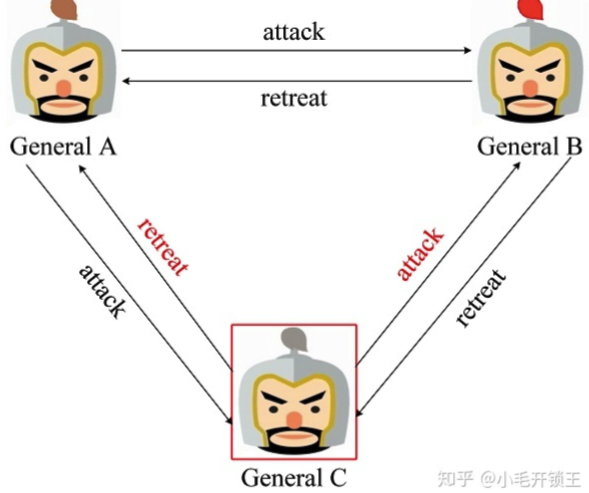
此时三位将军得到的指令如下(1：千万不要忘了自己的一票 2：将军C是叛徒，所有其肯定不会进攻的)：

将军A，进攻：撤退=1：2，最终撤退
将军B，进攻：撤退=2：1，最终进攻

最终将军B自己进攻成为炮灰。为了避免将军B成为炮灰，就需要我们的分布式算法了，针对该场景有如下两种：

口信消息型拜占庭问题之解
签名消息型拜占庭问题之解

这也正是我们本文要分析的主题，下面我们就开始吧！

2：口信消息型拜占庭问题之解

我们先来看下口信消息型拜占庭问题的要求，如果不满足要求该算法无法正常工作：

1：所有的消息都能够正常传递，不会丢失
2：叛徒数是已知的，假定为m，则此时总的将军数（包括叛徒）必须>=3m+1(推导出的结果，不用管是怎么推到的，公式嘛，记住就行了)

好，接下来正式开始，假定现在叛徒数一个，一共执行2轮消息传递，如下：

1：第一轮先发送消息的将军为指挥官，其他的为副官，指挥官将自己的指令发送给每一个副官
2：第二轮每位副官将自己从指挥官那里收到的消息，分别发送给其他的副官

主要有两种情况，分别是指挥官是忠臣，指挥官是叛徒。分别来看下。

2.1：指挥官是忠臣

A是苏秦 B是楚 C是燕 D是齐，自己对应下。

假定第一轮指挥官发送的消息是进攻，如下图：

因为指挥官发送的是进攻，所以此时进攻和撤退的情况如下：

1：苏秦，进攻
2：齐，进攻1，未知2，所以齐此时状态不确定
3：燕，进攻1，未知2，所以燕此时状态不确定
4：楚，叛徒，不管他

接下来执行第二轮投票，假设叛徒楚为了打乱计划，分别向齐和燕发送了和指挥官指令相反的指令撤退,如下图：

此时进攻和撤退的情况如下：

1：苏秦，进攻
2：齐，进攻2，撤退1，所以齐进攻
3：燕，进攻2，撤退1，所以燕进攻
4：楚，叛徒，不管他

所以最终苏秦，齐，燕都进攻，没有问题。这个过程程序实现参考这里 ,运行程序最终进攻还是撤退结果如下：

A: attack
C:[retreat, attack, attack]
D:[retreat, attack, attack]

另，以上程序实现比较粗糙，欢迎你在此基础上进行优化，也欢迎你将自己的代码以留言的方式分享给我，共同学习，共同进步。

2.1：指挥官是叛徒

A是苏秦 B是楚 C是燕 D是齐，自己对应下。

假定第一轮叛徒楚发送的消息是给CD的撤退，给A的进攻，如下图：

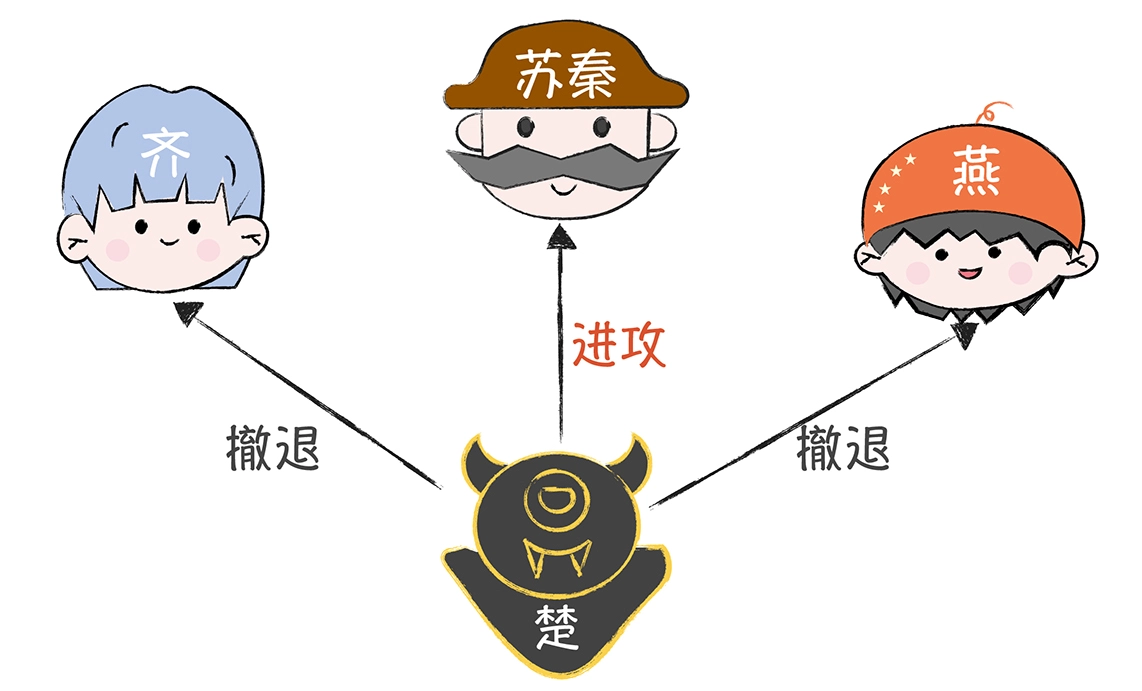
此时进攻和撤退的情况如下：

1：苏秦，进攻1 其他未知，因此行动不确定
2：齐，撤退1 其他未知，因此行动不确定
3：燕，撤退1 其他未知，因此行动不确定
4：楚，叛徒，不管他

第二轮，所有的忠臣，即苏秦，齐，燕分别发送自己收到的叛徒B的命令给其他将军,如下图：

此时进攻和撤退的情况如下：

1：苏秦，进攻1 撤退2，最终撤退
2：齐，进攻1 撤退2，最终撤退
3：燕，进攻1 撤退2，最终撤退
4：楚，叛徒，不管他

所以最终苏秦，齐，燕都撤退，没有问题。这个过程程序实现参考这里 ,运行程序最终进攻还是撤退结果如下：

C:[attack, retreat, retreat]
A:[retreat, retreat, attack]
D:[attack, retreat, retreat]

另，以上程序实现比较粗糙，欢迎你在此基础上进行优化，也欢迎你将自己的代码以留言的方式分享给我，共同学习，共同进步。

// TODO 补充2个叛徒7个将军的场景是怎样的一个过程？？？

3：签名消息型拜占庭问题之解

因为签名消息型需要用到签名消息的内容，因此我们需要先来看下签名消息的内容，接着再来看什么是签名消息型拜占庭问题之解。

3.1：签名消息

签名消息是带有数字签名的消息，而数字签名可以理解为合同上的公章，可以起到辨别真伪的作用，因此计算机的公章就是数字签名，通过签名消息，可以实现消息的完整性（接收方对比解密摘要）和不可抵赖（发送方不可抵赖，因为只有自己能生成数字签名），比如Bob要给Alice发送一句话我已经到北京了,则数字签名的过程就是这样的，首先通过hash函数生成摘要（后续用来保证完整性）,然后通过加密算法生成数字签名，如下图：

Alice收到消息后按照如下操作验证消息是否篡改，首先通过自己公钥解密消息，生成摘要（如果不能正常解密，也说明消息可能被篡改），然后使用原始消息生成摘要，对比二者，如果正常，则消息正常，否则不正常，如下图：

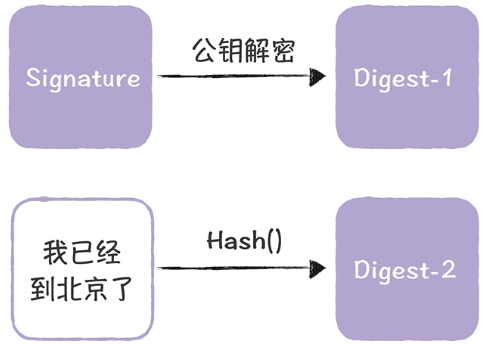
源码 实现。

3.2：具体实例

签名消息型拜占庭问题需要注意如下内容：

1：n个将军，能够容忍n-2个判将
2：如果判将数是m，则需要m+1轮消息
3：所有忠诚的将军将收到的信息去重排序后，假设有n个元素，则n/2，即取整，按下标0开始，从排序结果中获取要执行的指令，所以这种算法，只保证所有的将军执行相同的指令，但不一定是正确的指令，但是这也是一种共识
4：因为使用了数字签名，所以任何被篡改的消息都能被识别，并丢弃

简单起见，本文以2忠1叛为例进行说明，首先看忠诚将军先发消息的场景，如下将军A先发消息给将军B和将军C，然后将军B和将军C分别将从将军A收到的指令发给对方，但将军B是叛徒其会篡改将军A的指令，此时将军B将会发现将军A的指令被篡改，丢弃该消息，如下图：

该场景源码实现参考这里 ,运行结果说明如下：

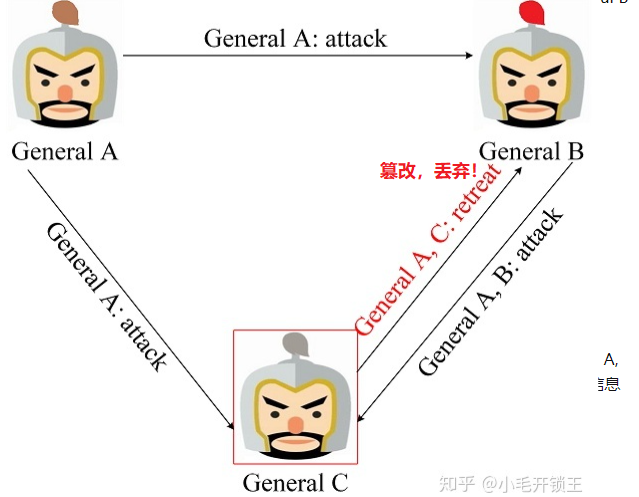
然后我们看下叛徒先发消息的场景，叛徒C想要达到扰乱的目的就只能发送不同的消息给将军A和将军B，比如发送攻击消息给将军A,发送撤退消息给将军B，但是在第二轮将军A和将军B互发消息后，发现第一轮将军A发送给了彼此不同的消息，则会判断出将军C是叛徒，然后丢弃消息，执行某约定指令，如撤退，该过程如下图：

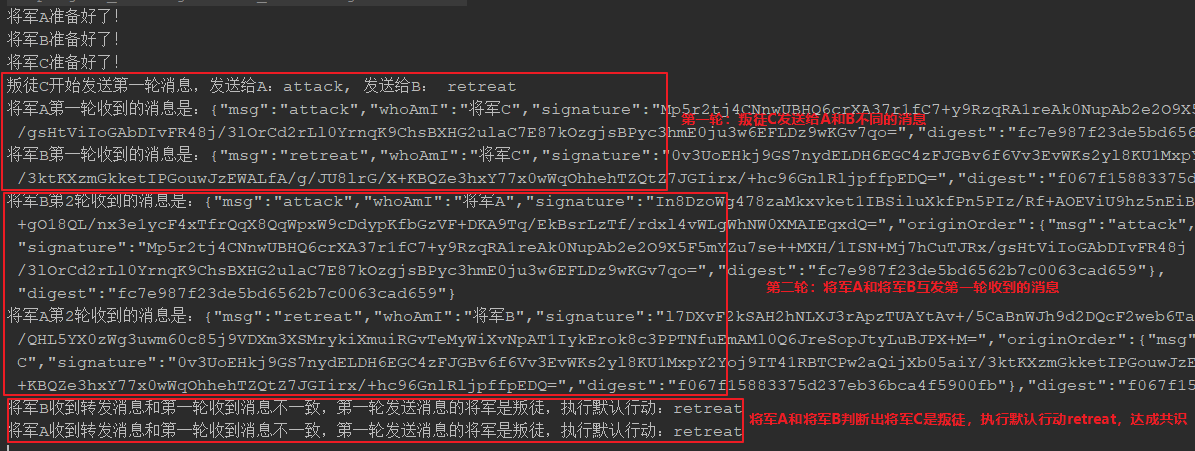
该场景源码实现参考这里 ,运行结果说明如下：

写在后面

参考文章列表

拜占庭将军问题 (The Byzantine Generals Problem) 。

https之数字证书分析 。