C++_012_数据结构_栈_顺序表储存版

栈

    这里只写顺序表存储版本的栈，链式存储参考上一篇博客《C++_011_数据结构_循环双链表_混合链表》的写法，这里不做赘述。

    除此之外，本篇给出一些关于栈的常用算法。

    栈其实就是线性表的变种，只不过，只能在线性表的尾部插入和删除。

包含的主要知识点

1.栈的线性存储写法。

2.用栈写多种类型括号匹配的算法。

3.十进制转任意进制的算法。

运行截图

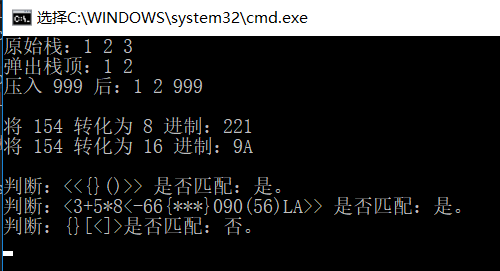
主函数

// 栈_普通版.cpp : 定义控制台应用程序的入口点。
//

#include "stdafx.h"
#include"Stack.cpp"
void Conversion(Stack<int> &a , int num, int r);//十进制转化为 r 进制后存储在栈中。
bool brackets(char s[]);//检测括号匹配。

int main()
{
	int arr[3] = { 1,2,3 };
	Stack<int> a(arr,3);
	cout <<"原始栈："<< a;
	a.Pop();
	cout << "弹出栈顶：" << a;
	a.Push(999);
	cout << "压入 999 后：" << a << endl;

	Stack<int> b;
	cout << "将 154 转化为 8 进制：";
	Conversion(b, 145, 8);
	cout << endl;
	Stack<int> c;
	cout << "将 154 转化为 16 进制：";
	Conversion(b, 154, 16);
	cout << endl<<endl;

	cout << "判断：<<{}()>> 是否匹配：";
	char s1[] = "<<{}()>>";
	if (brackets(s1))
	{
		cout << "是。" << endl;
	}
	else
	{
		cout << "否。" << endl;
	}

	cout << "判断：<3+5*8<-66{***}090(56)LA>> 是否匹配：";
	char s2[] = "<3+5*8<-66{***}090(56)LA>>";
	if (brackets(s2))
	{
		cout << "是。" << endl;
	}
	else
	{
		cout << "否。" << endl;
	}

	cout << "判断：{}[<]>是否匹配：";
	char s3[] = "{}[<]>";
	if (brackets(s3))
	{
		cout << "是。" << endl;
	}
	else
	{
		cout << "否。" << endl;
	}
	getchar();
    return 0;
}

void Conversion(Stack<int> &a, int num, int r)
{
	char base[17] = { '0','1','2','3','4','5','6','7','8','9','A','B','C','D','E','F' };
	while (num)
	{
		a.Push(num%r);
		num /= r;
	}
	while (!a.IsEmpty())
	{
		cout << base[a.Pop()];
	}
}

bool brackets(char s[])
{
	/*四种括号： ()  {}  [] <>  */
	/*遇到括号就入栈，最后看是否对称。*/

	Stack<char>  a;
	for (int i = 0; s[i] != '\0'; i++)
	{
		
		switch (s[i])
		{
			case '(':
			{
				a.Push('(');
				break;
			}
			case ')':
			{
				if (a.Pop() != '(')
				{
					return false;
				}
				break;
			}
			case '{':
			{
				a.Push('{');
				break;
			}
			case '}':
			{
				if (a.Pop() != '{')
				{
					return false;
				}
				break;
			}
			case '[':
			{
				a.Push('[');
				break;
			}
			case ']':
			{
				if (a.Pop() != '[')
				{
					return false;
				}
				break;
			}
			case '<':
			{
				a.Push('<');
				break;
			}
			case '>':
			{
				if (a.Pop() != '<')
				{
					return false;
				}
				break;
			}
			default:
			{
				continue ;
			}
		}

	}
	if (a.IsEmpty())
	{
		return true;
	}
	else
	{
		return false;
	}
}

栈的头文件

#pragma once
#include<iostream>
#include<ostream>
using namespace std;
#define MaxSize 100

template<typename T>
class Stack;

template<typename T>
ostream& operator<< (ostream& out, Stack<T> & a);

template<typename T>
class Stack
{
public:
	Stack();//默认构造函数
	Stack(T a[],int Length);//含参构造函数。
	~Stack();//析构函数
private:
	int Top;//栈顶
	T Data[MaxSize];//数据
public:
	void InitStack();//初始化操作函数。
	void DestroyStack();//销毁栈。
	void Push(T Obj);//压栈。
	T Pop();//弹出栈顶。
	T GetTop();//获取栈顶数据。
	bool IsEmpty();//判断是否为空栈。
	bool IsFull();//判断栈是否满。
	int GetSize();//获取栈存储数据的总个数。

	friend ostream& operator<< <>(ostream& out, Stack<T> & a);//输出函数。
};

template<typename T>
ostream & operator<< (ostream & out, Stack<T>& a)
{
	for (int i = 0; i <= a.Top; i++)
	{
		out << a.Data[i] << " ";
	}
	out << endl;
	return out;
}

源文件

#include "stdafx.h"
#include "Stack.h"

template<typename T>
Stack<T>::Stack()
{
	Top = -1;
}

template<typename T>
Stack<T>::Stack(T a[], int Length)
{
	if (Length<0 || Length>MaxSize)
	{
		throw "Stack(T a[],int Length) wrong.\n";
	}
	for (Top = 0; Top < Length; Top++)
	{
		Data[Top] = a[Top];
	}
	Top--;
}

template<typename T>
Stack<T>::~Stack()
{
	Top = -1;
}

template<typename T>
void Stack<T>::InitStack()
{
	cout << "初始化栈，这里不需要初始化。" << endl;
}

template<typename T>
void Stack<T>::DestroyStack()
{
	Top = -1;
}

template<typename T>
void Stack<T>::Push(T Obj)
{
	Data[Top+1] = Obj;
	Top++;
}

template<typename T>
T Stack<T>::Pop()
{
	Top--;
	return Data[Top+1];
}

template<typename T>
T Stack<T>::GetTop()
{
	return Data[Top];
}

template<typename T>
bool Stack<T>::IsEmpty()
{
	return Top<0?true:false;
}

template<typename T>
bool Stack<T>::IsFull()
{
	return Top > MaxSize - 1 ? true: false ;
}

template<typename T>
int Stack<T>::GetSize()
{
	return Top+1;
}