数据结构树(Tree)详解

树型结构是一类重要的非线性数据结构。其中以树和二叉树最为常用，直观看来，树是以分支关系定义的层次结构。树结构在客观世界中广泛存在，如人类社会的族谱和各种社会组织机构可用树来形象表示。

树的定义和基本术语

定义：

树（Tree** 是由一个集合以及在该集合上定义的一种关系构成的。集合中的元素称为树的结点，所定义的关系称为父子关系。父子关系在树的结点之间建立了一个层次结构。在这种层次结构中有一个结点具有特殊地位，这个结点称为该树的根结点，或简称树根。

术语：

• 节点的度：一个节点含有的子树的个数称为该节点的度；
• 树的度：一棵树中，最大的节点度称为树的度；
• 叶节点或终端节点：度为零的节点；
• 非终端节点或分支节点：度不为零的节点；
• 父亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点；
• 孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点；
• 兄弟节点：具有相同父节点的节点互称为兄弟节点；
• 节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推；
• 深度：对于任意节点n,n的深度为从根到n的唯一路径长，根的深度为0；
• 高度：对于任意节点n,n的高度为从n到一片树叶的最长路径长，所有树叶的高度为0；
• 堂兄弟节点：父节点在同一层的节点互为堂兄弟；
• 节点的祖先：从根到该节点所经分支上的所有节点；
• 子孙：以某节点为根的子树中任一节点都称为该节点的子孙。
• 森林：由m（m>=0）棵互不相交的树的集合称为森林；

树的种类

• 无序树：树中任意节点的子节点之间没有顺序关系，这种树称为无序树，也称为自由树；
• 有序树：树中任意节点的子节点之间有顺序关系，这种树称为有序树；
  • 二叉树：每个节点最多含有两个子树的树称为二叉树；
    • 完全二叉树：对于一棵二叉树，假设其深度为d（d>1）。除了第d层外，其它各层的节点数目均已达最大值，且第d层所有节点从左向右连续地紧密排列，这样的二叉树被称为完全二叉树；
      • 满二叉树：所有叶节点都在最底层的完全二叉树；
    • 平衡二叉树（AVL树）：当且仅当任何节点的两棵子树的高度差不大于1的二叉树；
    • 排序二叉树(二叉查找树（英语：Binary Search Tree))：也称二叉搜索树、有序二叉树；
  • 霍夫曼树：带权路径最短的二叉树称为哈夫曼树或最优二叉树；
  • B树：一种对读写操作进行优化的自平衡的二叉查找树，能够保持数据有序，拥有多于两个子树。

有序树和无序树

如果树中结点的子树从左到右看，谁在左边，谁在右边，是有规定的，这棵树称为有序树；反之称为无序树。

在有序树中，一个结点最左边的子树称为"第一个孩子"，最右边的称为"最后一个孩子"。

二叉树

定义：

二叉树（英语：Binary tree）是每个节点最多只有两个分支（即不存在分支度大于2的节点）的树结构。通常分支被称作“左子树”或“右子树”。二叉树的分支具有左右次序，不能随意颠倒。

与普通树不同，普通树的节点个数至少为1，而二叉树的节点个数可以为0；普通树节点的最大分支度没有限制，而二叉树节点的最大分支度为2；普通树的节点无左、右次序之分，而二叉树的节点有左、右次序之分。

二叉树通常作为数据结构应用，典型用法是对节点定义一个标记函数，将一些值与每个节点相关系。这样标记的二叉树就可以实现二叉搜索树和二叉堆，并应用于高效率的搜索和排序。

简单地理解，满足以下两个条件的树就是二叉树：

• 本身是有序树；
• 树中包含的各个节点的度不能超过 2，即只能是 0、1 或者 2；

二叉树的性质：

经过前人的总结，二叉树具有以下几个性质：

• 二叉树中，第 i 层最多有 2i-1 个结点。
• 如果二叉树的深度为 K，那么此二叉树最多有 2K-1 个结点。
• 二叉树中，终端结点数（叶子结点数）为 n0，度为 2 的结点数为 n2，则 n0=n2+1。

完全二叉树

如果二叉树中除去最后一层节点为满二叉树，且最后一层的结点依次从左到右分布，则此二叉树被称为完全二叉树。

满二叉树

二叉树还可以继续分类，衍生出满二叉树和完全二叉树,如果二叉树中除了叶子结点，每个结点的度都为 2，则此二叉树称为满二叉树。

满二叉树除了满足普通二叉树的性质，还具有以下性质：

• 满二叉树中第 i 层的节点数为 2n-1 个。
• 深度为 k 的满二叉树必有 2k-1 个节点 ，叶子数为 2k-1。
• 满二叉树中不存在度为 1 的节点，每一个分支点中都两棵深度相同的子树，且叶子节点都在最底层。
• 具有 n 个节点的满二叉树的深度为 log2(n+1)。

平衡二叉树（AVL树）

对于这棵树里的每个节点，它的左子树和右子树的高度差不大于 1。这里要注意，是对于每个节点，而不只是对于根结点。比如左边这棵树就不是平衡二叉树，右边的才是。

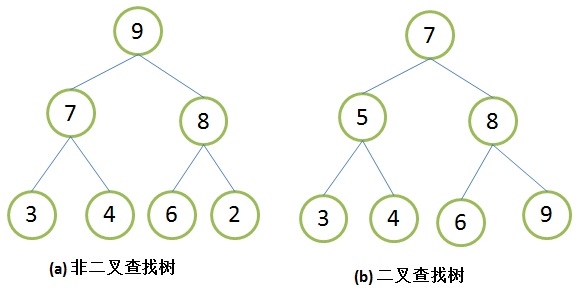
排序二叉树(二叉查找树）

二叉查找树（英语：Binary Search Tree），也称为二叉查找树、有序二叉树（ordered binary tree）或排序二叉树（sorted binary tree），是指一棵空树或者具有下列性质的二叉树：

• 若任意节点的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
• 若任意节点的右子树不空，则右子树上所有节点的值均大于或等于它的根节点的值；
• 任意节点的左、右子树也分别为二叉查找树；

简单的理解，对于这棵树里的每个节点，它左子树里的每个节点的值都小于它的值；它右子树里的每个节点的值都大于它的值。

---

欢迎关注公众号： 编码是个技术活