想象:
- 有一滩牌,现在还是一滩,因为还没堆起来。
- 老师对小明说:“来,给咱们把这一滩牌整理好,最大的放最上面,按大小顺序堆起来”。
- 小明很聪明立刻找出最大的,然后……
- stop!!老师说:这样眼睛太累了,你把牌全看一遍才找出一个大的……我要求你每次最多只能看3张牌,给我把顺序排好。
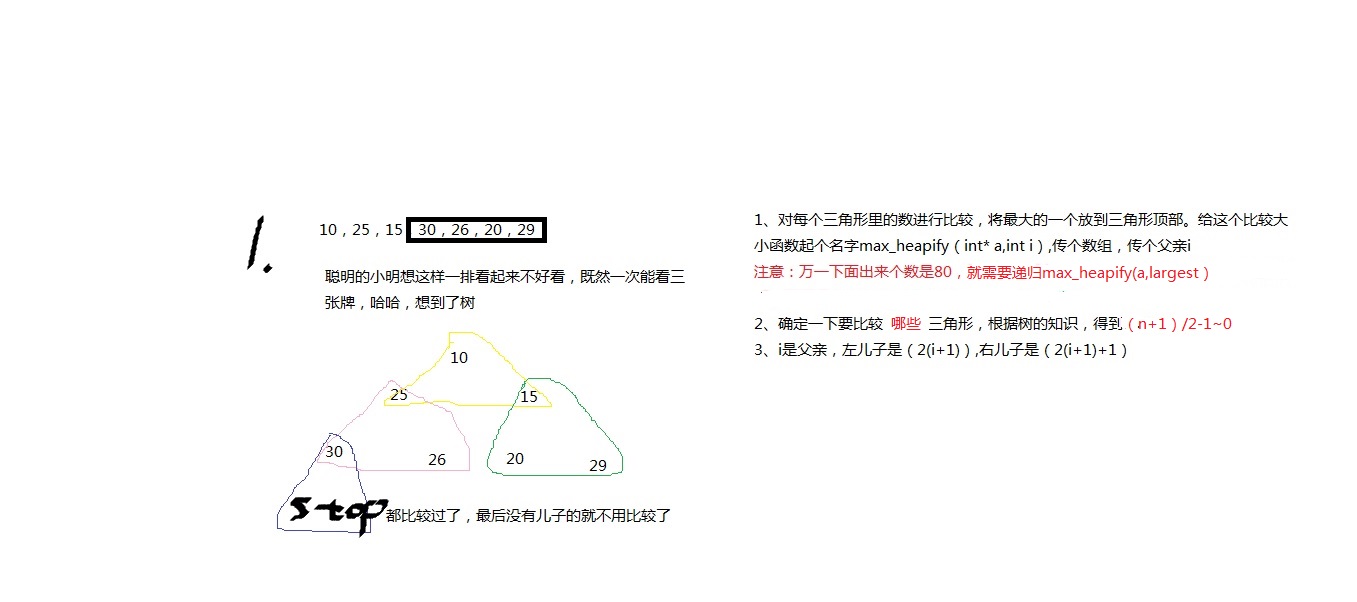
- 小明想起了堆排序,不一会儿就做好了。
程序流程如下:
1.建堆
2.堆排序
#include < iostream>
using namespace std;
//a是传过来的数组,i是待调整的节点,m是堆的范围
void max_heapify(int* a,int i,int m)
{
int largest=i;
int temp;
int l=2*i+1;//左儿子
int r=l+1;//右儿子
//找出最大值的索引
if(l<=m&&a[i]<a[l])
largest=l;
if(r<=m&&a[largest]<a[r])
largest=r;
//交换,将最大值放在顶部
if(largest!=i)
{
temp=a[i];
a[i]=a[largest];
a[largest]=temp;
max_heapify(a,largest,m);//a[largest]可能不符合要求,所以进行递归调整
}
}
//堆排序,每次将第一个数(最大),与最后一个数交换,也就是将最大值放到了正确位置
//并对堆得大小也就是m值减1,因为最后一个数不再参加调整
//每次需对第一个也就是a[0]进行调整,让树保持堆的特性
void heapsort(int* a,int n,int m)
{
for(int i=n;i>0;i--)
{
//第一个数与最后一个数交换
int temp;
temp=a[i];
a[i]=a[0];
a[0]=temp;
max_heapify(a,0,--m);//最后一个不参加调整,故m-1
}
}
int main(void)
{
//利用大根堆进行排序
int a[7]={10,25,15,30,26,20,29};
int m=6;//m用来保存数组的大小,在后面也表示堆得调整范围
//建堆,从下往上建,从非叶子结点开始i=7/2-1=2
for(int i=2;i>=0;i--)
{
max_heapify(a,i,m);//调整树,使其保持堆的特性(父大于子)
}
heapsort(a,6,m);//对调整好的树进行堆排序
//输出排好的数
for(i=0;i<7;i++)
cout<<" "<<a[i];
return 0;
}






















 25万+
25万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








