Python实现可自定义更新策略的LRU Cache

LRU Cache

　　LRU(Least Recently Used)，直译为“最近最少使用”，其实称“最久未被使用”更为恰当。这是一个非常重要的算法，在学操作系统的时候第一次遇见，在做leetcode的时候再次遇见，知道是用于做缓存的页面置换。但是LRU不仅仅用于这一个用途，凡是有数据更新策略的应用，LRU都可以是候选算法。比如redis、memcached、oracle等缓存和数据库、或在其它应用场景方面也有类似的需求。总之要达到的目的是：保持新鲜，剔除陈旧，减少交换。
　　
- 算法原理
　　需求描述：
　　实现LRU算法，主要工作是实现LRU Cache的数据结构，或者说实现这种类。lru缓存的主要操作有两个，一个是get，获取数据是否在cache中，如果在，则把该数据放到缓存最前面；另一个的主要操作是set，在缓存中存放某个值，并且存放到最前面，如果缓存中有这个值，则更新，如果缓存满了，则删除缓存中最后面的值。总之，缓存中最前面的值是最近被使用过的，缓存有大小限制，超出要删除最久未被使用的值。要求所有操作时间复杂度均为o(1)。
　　分析：
　　直觉看上去，数据从近到远以此排列，这是一个线性结构，列表（顺序线性表/数组），链表，队列，栈？
　　先考虑目的要求，要求最近使用的在最前，最久未使用的在最后，队列是FIFO的结构，栈是FILO的结构，都不符合要求。
　　再考虑数据更新，要求o(1)复杂度下，把数据更新到最前面。列表被排除，无法满足要求。只有链式结构才可以在o(1)下完成更新。
　　最后考虑数据查找，链式结构下，数据查找复杂度为o(n)，又不能满足o(1)的复杂度。看来必须依赖其它数据结构的辅助。
　　用列表完成o(1)的更新，不可能啊，想想看，将数组中一个位置的数挪到最前面，那这个位置之前的数据都要后移一位，怎样都不能实现o(1)的开销。那就考虑链式结构下如果实现o(1)的查找吧。通常情况下，查找链表中一个位置上的值，需要从头结点开始，依次后移查找。如果有尾结点也一样依次向前移动，时间复杂度为o(n)。那么我们能不能将每个结点的位置记下来，直接去存放结点的那个位置查找呢？哈希表派上了用场。哈希表存放结点位置的对应关系，能够满足o(1)下的数据查找，同时链表能够实现o(1)的数据更新，符合预想的要求。
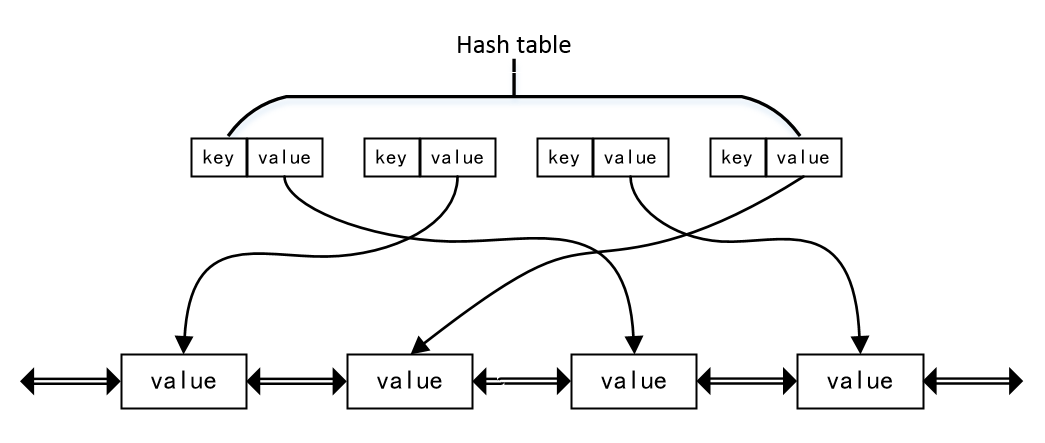
　　总结：在Cache结构中，需要一个hash table，用于存放位置关系，需要一个链表，用于更新数据，链表我们使用双向链表。大体结构为：
　　

class LRU:
    var table = {}