李宏毅机器学习笔记（5）： Classification：Probabilistic Generative Model

Classification：Probabilistic Generative Model

分类问题属于比较常见的问题之一了，这次李老师讲的是一个比较基础的分类问题的模型，为了让我们对这个问题进一步了解，可以更好地继续学习。

1 分类

分类问题是通过对大量输入进行分析，寻找模型，将样本进行分类，从而之后输入的样本，可以分类到合适的类。这个问题还是很容易理解的，看例子：

接下来对宝可梦的属性进行分类。

当然，首先要做的还是统计每一个宝可梦的不同属性参数。每一个宝可梦就是样本，这部分其实是在统计样本的特征。

有一种错误观点，把分类问题看作回归问题，将分类问题的多个类看成不同的数值区间，对各种参数拟合，看样本拟合的最终参数与哪个类的距离最小，确定所属类。然而，这样的处理方法有很大问题，如下图：当存在右下角的点时，回归问题会把这些点当作误差进行处理，而实际上这些点可以进行分类，如果强行进行回归，将出现减小误差，图1-1中红色箭头区域。

图1-1 把分类问题看成回归问题是错误的

同时，这样使用的话，会默认不同的类之间会有一些数值上的距离关系，比如类1为1，类2为2，类3为3，这样会默认类1和类2的相似度是比类1和类2相似度小的，而实际可能并没有这种关系。

2 理想方式

接下来讨论理想的分类问题的解决方式：

我们希望寻找一个函数，如果把数据带入发现输出值大于0就判断是类1，否则是类2，0就能理解为区分类1与类2的一种分界线。

模型如下：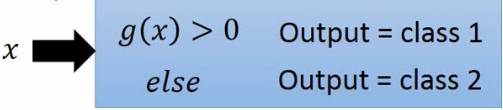

那么我们的损失函数需要指示我们分类错误的值，如下，如果输出的分类判决和实际的分类不同，那么δ函数就取值为1。

损失函数如下：

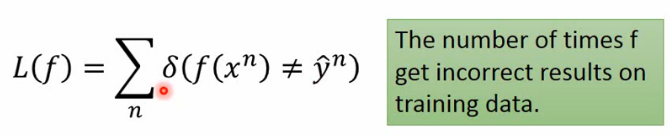
其实如何选择函数最直观的理解就是，在训练集上错误次数越小，说明越符合。这就是分类问题的初步的大致框架，目前分类问题的模型有很多，比如：perceptron、SVM。

为了介绍我们今天要聊的模型，我们使用概率的观点去看待分类问题，如下图2-1，有两个盒子，盒子中有不同的球，很容易得到不同的摸球概率。

图2-1 摸球问题

很容易就知道，如有一个蓝球，那么这个球是来自盒子1的概率是多少。使用贝叶斯公式可以轻松知道答案。跟着上文的分析，我们可以类比出分类问题。

图2-2 类比分类问题

如图2-2，实际分类问题中，可以从样本集中求得图中画红框的概率，那么我们就可以使用贝叶斯公式求出每一个样本的条件概率（就是抽出样本x属于类1的概率），也可以使用全概率公式求出样本x的概率，这里我们称之为生成模型。接下来回到我们的例子如下图2-3。（这里的样本x是不知道属于哪一类的）

图2-3 宝可梦的分类问题

对于我们这个分类问题，我们姑且先考虑二分类模型，只分类水系和一般系的，分类好测试和训练集，训练集中的数目为79只水系的，61只一般系的。那么就可以先计算出每种出现的概率（图2-3）。

继续可以按照上文中的方式进行下一步：

图2-4 宝可梦的分类问题

此时我们需要做的就是，提供一只新的宝可梦（这只宝可梦并不在我们已知的79种水系，即上图的海龟，原谅我不知道它叫什么名字），现在我们需要知道这只宝可梦属于水系的概率是多少。对每个水系的宝可梦的特征我们可以用一个向量表示。如图2-4，这里只选择了防御力和特殊防御力做代表，可以看出把79个宝可梦的特征画在了图上，这边标注出了可达鸭、杰尼龟和这只小海龟。我们需要求这只小海龟属于水系的概率，这个概率当然不可能是0。

图2-4 宝可梦的特征向量

接下来我们需要假设我们的点服从高斯分布，这些概率论很基础的就不提啦。要注意的是这里的高斯分布的方差部分要使用协方差矩阵：

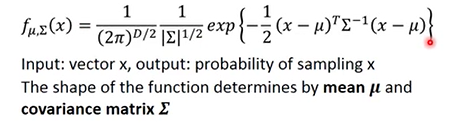
之后使用高斯分布，我们就可以使用高斯分布的概率密度函数，对未知的宝可梦属于水系的概率进行求解，可以看下图2-5进行理解，如果新的x离红色圈中心越近，说明概率越大。那么为了进行估计，我们需要找到这个概率密度函数的均值与协方差矩阵。

图2-5 概率

我们知道，要把这79个点使用高斯分布进行包含，理论上这个高斯分布有无穷多个，不同的均值和协方差矩阵组成的分布都不一样，如图2-6，以右上角红圈为中心的高斯分布和左下角的高斯分布都是可以进行表示。但是这左下角肯定是优于右上角的，那么我们怎么选取最优的呢？

图2-6 最大似然估计

这里我们就可以使用最大似然估计（学过信号检测与估值或者信息论，数理统计等这类科目应该对这个很了解了）。最大似然估计就是一种比较普遍的估计参量的方法，本文结合这个问题来做阐述，系统的学移步概率论与数理统计。我们可以这样理解，每一个均值与协方差矩阵对应的高斯分布都是不同的，每一个已知样本在这些高斯分布中都能求出他们的概率，那么他们一起出现（当前实际情况）的概率就是他们每一个概率的乘积。我们找的高斯分布其实就是使当前情况概率达到最大，也就是最适合当前这79个点的概率分布。

我们把这79个点的概率密度函数的乘积叫做似然函数（图2-6最下面的公式），最大似然估计也就是寻找参数让似然函数达到最大的估计。最大似然估计在很多情况下用处很多。

最大似然估计的解法也很简单，由于我们的分布为高斯分布，基本上大多求法就是对似然函数先求对数，后求导求极值。

图2-7 最大似然估计结果

最后求出的结果，图2-7最下面的两个式子分别是均值和协方差矩阵的最优。

接着求normal类的，如图2-8。

图2-8 两类结果

有了两类模型接下来就可以进行分类啦。

3 进行分类

终于，我们得到了模型，可以进行分类了，如图3-1。我们需要求出如果出现x，那么这个x处于C1的概率，即为P(C1|x)。这个概率可以用贝叶斯公式求得，贝叶斯公式每个值上文都已知了。求出这个概率我们就可以对其进行判决，如果这个概率高于某一个阈值，就评定属于C1类，图中这个阈值是0.5。（这个阈值的选取方法其实也有挺多的，这里老师没有提，暂且先不说了，之后应该会有提到）

图3-1 如何分类

查看结果吧，图3-2，红色点是一般系，蓝色点是水系，纵坐标是特殊防御力，横坐标是一般防御力。左上图是处于不同位置的点的P(C1|x)。右上图是训练集上的划分，由下图是测试集上的划分，其中蓝色区域判定为水系，红色区域判定为一般系。结果发现，测试集只有47%的准确率，分类的效果好差啊。我们应该把维度提升到7个维度进行分类，也只有54%。

图3-2 结果

4 模型修正

为了让效果更好，对模型进行修正，如图4-1。对于两个不用的高斯分布，此时我们取相同的协方差矩阵，均值和上文相同。

进行新的最大似然估计，得到结果均值与之前相同，协方差矩阵这里对原先的进行了加权平均。

下图4-1中右上角的参考书是pattern recontignition and mechine learning。

图4-1 模型修正

进行对比发现，使用相同的协方差矩阵使得了分界线成为了线性的了，而在7个维度的准确率上升到了73%。这里老师并没有解释为什么变好了，他说7维空间我们也很难去理解，这可能就是机器学习的优势吧。

图4-2 模型修正后结果

5 总结

这章使用了三步去完成分类问题：

1. 模型建立，使用贝叶斯公式与判决。
2. 优劣性判决，最大似然估计。在第二次修正时把两个协方差矩阵统一了。
3. 最后寻找最好的模型。

还有一些问题：

其实在本模型中使用了高斯分布，这个分布也不一定是高斯分布，很多情况下这个分布我们会根据不同情况下进行不同的设计。比如：如果样本很明显是二分类，那我们就可以使用贝努力分布去做了。

最后我们对后验概率进行一些分析：后验概率就是上文中提到的P(C1|x)。之后进行数学推导，不想看的直接跳到结论。（数学推导在视频的61：08）

结论：经过李老师数学推导，可以看到后验概率等于关于z的sigmoid函数（数学推导第一页ppt上有这个函数图像），如果协方差相等，z可以约掉一些项，得到一个有关x的一次函数式，为了更方便求解，那么我们可不可以直接去求这个一次函数呢？求解一次函数实际上就是求函数的斜率与截距，下一节这个问题会被解答。