Python3-Scikit-image

参考：

1、http://www.scipy-lectures.org/packages/scikit-image/index.html

2、http://scikit-image.org/docs/dev/

Chapters contents

• Introduction and concepts
  • scikit-image and the SciPy ecosystem
  • What’s to be found in scikit-image
• Input/output, data types and colorspaces
  • Data types
  • Colorspaces
• Image preprocessing / enhancement
  • Local filters
  • Non-local filters
  • Mathematical morphology
• Image segmentation
  • Binary segmentation: foreground + background
  • Marker based methods
• Measuring regions’ properties
• Data visualization and interaction
• Feature extraction for computer vision
• Full code examples
• Examples for the scikit-image chapter

———————————————————————————————————————————————————

3.3.1. Introduction and concepts

Images are NumPy’s arrays np.ndarray

image:	np.ndarray
pixels:	array values: a[2, 3]
channels:	array dimensions
image encoding:	dtype (np.uint8, np.uint16, np.float)
filters:	functions (numpy, skimage, scipy)

import numpy as np
import matplotlib.pyplot as plt

check = np.zeros((9, 9))
check[::2, 1::2] = 1
check[1::2, ::2] = 1
plt.matshow(check, cmap='gray')
plt.show()

—————————————————————————————————————————————————————————————————————————————

3.3.1.1. scikit-image and the SciPy ecosystem

import skimage
>>> from skimage import data  # most functions are in subpackages

Most scikit-image functions take NumPy ndarrays as arguments

>>>

>>> camera = data.camera()
>>> camera.dtype
dtype('uint8')
>>> camera.shape
(512, 512)
>>> from skimage import filters
>>> filtered_camera = filters.gaussian(camera, 1)
>>> type(filtered_camera)   
<type 'numpy.ndarray'>

Other Python packages are available for image processing and work with NumPy arrays:

• scipy.ndimage : for nd-arrays. Basic filtering, mathematical morphology, regions properties
• Mahotas

Also, powerful image processing libraries have Python bindings:

• OpenCV (computer vision)
• ITK (3D images and registration)
• and many others

(but they are less Pythonic and NumPy friendly, to a variable extent).

import skimage
from skimage import data  # most functions are in subpackages

camera = data.camera()
print(camera.dtype,camera.shape) # uint8 (512, 512)

from skimage import filters
filtered_camera = filters.gaussian(camera, 5)
print(type(filtered_camera)) # <class 'numpy.ndarray'>

import matplotlib.pyplot as plt

plt.subplot(121)
plt.imshow(camera)
plt.title('original')
plt.axis('off')

plt.subplot(122)
plt.imshow(filtered_camera)
plt.title('filter')
plt.axis('off')

plt.show()

—————————————————————————————————————————————————————————————————————————————

3.3.1.2. What’s to be found in scikit-image

• Website: http://scikit-image.org/
• Gallery of examples: http://scikit-image.org/docs/stable/auto_examples/

Different kinds of functions, from boilerplate utility functions to high-level recent algorithms.

• Filters: functions transforming images into other images.

  • NumPy machinery
  • Common filtering algorithms

• Data reduction functions: computation of image histogram, position of local maxima, of corners, etc.

• Other actions: I/O, visualization, etc.

—————————————————————————————————————————————————————————————————————————————

3.3.2. Input/output, data types and colorspaces

I/O: skimage.io

>>>

>>> from skimage import io

Reading from files: skimage.io.imread()

>>>

>>> import os
>>> filename = os.path.join(skimage.data_dir, 'camera.png')
>>> camera = io.imread(filename)

Works with all data formats supported by the Python Imaging Library (or any other I/O plugin provided to imread with the plugin keyword argument).

Also works with URL image paths:

>>>

>>> logo = io.imread('http://scikit-image.org/_static/img/logo.png')

Saving to files:

>>>

>>> io.imsave('local_logo.png', logo)

(imsave also uses an external plugin such as PIL)

import matplotlib.pyplot as plt
from skimage import data

camera = data.camera()


plt.figure(figsize=(4, 4))
plt.imshow(camera, cmap='gray', interpolation='nearest')
plt.axis('off')

plt.tight_layout()
plt.show()

—————————————————————————————————————————————————————————————————————————————

3.3.2.1. Data types

Image ndarrays can be represented either by integers (signed or unsigned) or floats.

Careful with overflows with integer data types

>>>

>>> camera = data.camera()
>>> camera.dtype
dtype('uint8')
>>> camera_multiply = 3 * camera

Different integer sizes are possible: 8-, 16- or 32-bytes, signed or unsigned.

 

An important (if questionable) skimage convention: float images are supposed to lie in [-1, 1] (in order to have comparable contrast for all float images)

>>>

>>> from skimage import img_as_float
>>> camera_float = img_as_float(camera)
>>> camera.max(), camera_float.max()
(255, 1.0)

Some image processing routines need to work with float arrays, and may hence output an array with a different type and the data range from the input array

>>>

>>> from skimage import filters
>>> camera_sobel = filters.sobel(camera)
>>> camera_sobel.max() 
0.591502...

Utility functions are provided in skimage to convert both the dtype and the data range, following skimage’s conventions: util.img_as_float,util.img_as_ubyte, etc.

See the user guide for more details.

An illustration of overflow problem arising when working with integers

import matplotlib.pyplot as plt
from skimage import data

camera = data.camera()
camera_multiply = 3 * camera

plt.figure(figsize=(8, 4))
plt.subplot(121)
plt.imshow(camera, cmap='gray', interpolation='nearest')
plt.axis('off')
plt.subplot(122)
plt.imshow(camera_multiply, cmap='gray', interpolation='nearest')
plt.axis('off')

plt.tight_layout()
plt.show()

———————————————————————————————————————————————————————————

3.3.2.2. Colorspaces

Color images are of shape (N, M, 3) or (N, M, 4) (when an alpha channel encodes transparency)

>>>

>>> face = scipy.misc.face()
>>> face.shape
(768, 1024, 3)

Routines converting between different colorspaces (RGB, HSV, LAB etc.) are available in skimage.color : color.rgb2hsv, color.lab2rgb, etc. Check the docstring for the expected dtype (and data range) of input images.

3D images

Most functions of skimage can take 3D images as input arguments. Check the docstring to know if a function can be used on 3D images (for example MRI or CT images).

Exercise

Open a color image on your disk as a NumPy array.

Find a skimage function computing the histogram of an image and plot the histogram of each color channel

Convert the image to grayscale and plot its histogram.

import numpy as np
from skimage import exposure,data
import matplotlib.pyplot as plt

image =data.camera()
hist1,bin_edges=np.histogram(image, bins=256)   #用numpy包计算直方图
hist2, bins_center=exposure.histogram(image, nbins=256)  #用skimage计算直方图
hist3= image.flatten()

plt.subplot(131)
plt.hist(hist1, bins=bin_edges, normed=1, facecolor='b',edgecolor='b')

plt.subplot(132)
plt.hist(hist2,bins_center, normed=1, facecolor='r',edgecolor='r')
# plt.plot(bins_center, hist2, lw=2)

plt.subplot(133)
n, bins, patches =plt.hist(hist3, bins=256, normed=1, facecolor='r',edgecolor='b')
plt.show()

———————————————————————————————————————————————————————————

3.3.3. Image preprocessing / enhancement

Goals: denoising, feature (edges) extraction, …
———————————————————————————————————————————————————

3.3.3.1. Local filters

Example : horizontal Sobel filter

Example : horizontal Sobel filter

>>>

>>> text = data.text()
>>> hsobel_text = filters.sobel_h(text)

Uses the following linear kernel for computing horizontal gradients:

1   2   1
0   0   0
-1  -2  -1

3.3.3.2. Non-local filters

Non-local filters use a large region of the image (or all the image) to transform the value of one pixel:

>>>

>>> from skimage import exposure
>>> camera = data.camera()
>>> camera_equalized = exposure.equalize_hist(camera)

Enhances contrast in large almost uniform regions.

3.3.3.3. Mathematical morphology

See wikipedia for an introduction on mathematical morphology.

Probe an image with a simple shape (a structuring element), and modify this image according to how the shape locally fits or misses the image.

Default structuring element: 4-connectivity of a pixel

>>>

>>> from skimage import morphology
>>> morphology.diamond(1)
array([[0, 1, 0],
       [1, 1, 1],
       [0, 1, 0]], dtype=uint8)

Erosion = minimum filter. Replace the value of a pixel by the minimal value covered by the structuring element.:

>>>

>>> a = np.zeros((7,7), dtype=np.uint8)
>>> a[1:6, 2:5] = 1
>>> a
array([[0, 0, 0, 0, 0, 0, 0],
       [0, 0, 1, 1, 1, 0, 0],
       [0, 0, 1, 1, 1, 0, 0],
       [0, 0, 1, 1, 1, 0, 0],
       [0, 0, 1, 1, 1, 0, 0],
       [0, 0, 1, 1, 1, 0, 0],
       [0, 0, 0, 0, 0, 0, 0]], dtype=uint8)
>>> morphology.binary_erosion(a, morphology.diamond(1)).astype(np.uint8)
array([[0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 1, 0, 0, 0],
       [0, 0, 0, 1, 0, 0, 0],
       [0, 0, 0, 1, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0]], dtype=uint8)
>>> #Erosion removes objects smaller than the structure
>>> morphology.binary_erosion(a, morphology.diamond(2)).astype(np.uint8)
array([[0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0]], dtype=uint8)

Dilation: maximum filter:

>>>

>>> a = np.zeros((5, 5))
>>> a[2, 2] = 1
>>> a
array([[ 0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  1.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.]])
>>> morphology.binary_dilation(a, morphology.diamond(1)).astype(np.uint8)
array([[0, 0, 0, 0, 0],
       [0, 0, 1, 0, 0],
       [0, 1, 1, 1, 0],
       [0, 0, 1, 0, 0],
       [0, 0, 0, 0, 0]], dtype=uint8)

Opening: erosion + dilation:

>>>

>>> a = np.zeros((5,5), dtype=np.int)
>>> a[1:4, 1:4] = 1; a[4, 4] = 1
>>> a
array([[0, 0, 0, 0, 0],
       [0, 1, 1, 1, 0],
       [0, 1, 1, 1, 0],
       [0, 1, 1, 1, 0],
       [0, 0, 0, 0, 1]])
>>> morphology.binary_opening(a, morphology.diamond(1)).astype(np.uint8)
array([[0, 0, 0, 0, 0],
       [0, 0, 1, 0, 0],
       [0, 1, 1, 1, 0],
       [0, 0, 1, 0, 0],
       [0, 0, 0, 0, 0]], dtype=uint8)

Opening removes small objects and smoothes corners.

Grayscale mathematical morphology

Mathematical morphology operations are also available for (non-binary) grayscale images (int or float type). Erosion and dilation correspond to minimum (resp. maximum) filters.

Higher-level mathematical morphology are available: tophat, skeletonization, etc.

See also

 

Basic mathematical morphology is also implemented inscipy.ndimage.morphology. The scipy.ndimage implementation works on arbitrary-dimensional arrays.

---

Example of filters comparison: image denoising

>>>

>>> from skimage.morphology import disk
>>> coins = data.coins()
>>> coins_zoom = coins[10:80, 300:370]
>>> median_coins = filters.median(coins_zoom, disk(1))
>>> from skimage import restoration
>>> tv_coins = restoration.denoise_tv_chambolle(coins_zoom, weight=0.1)
>>> gaussian_coins = filters.gaussian(coins, sigma=2)

3.3.4. Image segmentation

Image segmentation is the attribution of different labels to different regions of the image, for example in order to extract the pixels of an object of interest.

3.3.4.1. Binary segmentation: foreground + background

Histogram-based method: Otsu thresholding

 

The Otsu method is a simple heuristic to find a threshold to separate the foreground from the background.

Earlier scikit-image versions

skimage.filters is calledskimage.filter in earlier versions of scikit-image

from skimage import data
from skimage import filters
camera = data.camera()
val = filters.threshold_otsu(camera)
mask = camera < val

Labeling connected components of a discrete image

 

Once you have separated foreground objects, it is use to separate them from each other. For this, we can assign a different integer labels to each one.

Synthetic data:

>>>

>>> n = 20
>>> l = 256
>>> im = np.zeros((l, l))
>>> points = l * np.random.random((2, n ** 2))
>>> im[(points[0]).astype(np.int), (points[1]).astype(np.int)] = 1
>>> im = filters.gaussian(im, sigma=l / (4. * n))
>>> blobs = im > im.mean()

Label all connected components:

>>>

>>> from skimage import measure
>>> all_labels = measure.label(blobs)

Label only foreground connected components:

>>>

>>> blobs_labels = measure.label(blobs, background=0)

See also

 

scipy.ndimage.find_objects() is useful to return slices on object in an image.

3.3.4.2. Marker based methods

If you have markers inside a set of regions, you can use these to segment the regions.

Watershed segmentation

The Watershed (skimage.morphology.watershed()) is a region-growing approach that fills “basins” in the image

>>>

>>> from skimage.morphology import watershed
>>> from skimage.feature import peak_local_max
>>>
>>> # Generate an initial image with two overlapping circles
>>> x, y = np.indices((80, 80))
>>> x1, y1, x2, y2 = 28, 28, 44, 52
>>> r1, r2 = 16, 20
>>> mask_circle1 = (x - x1) ** 2 + (y - y1) ** 2 < r1 ** 2
>>> mask_circle2 = (x - x2) ** 2 + (y - y2) ** 2 < r2 ** 2
>>> image = np.logical_or(mask_circle1, mask_circle2)
>>> # Now we want to separate the two objects in image
>>> # Generate the markers as local maxima of the distance
>>> # to the background
>>> from scipy import ndimage
>>> distance = ndimage.distance_transform_edt(image)
>>> local_maxi = peak_local_max(distance, indices=False, footprint=np.ones((3, 3)), labels=image)
>>> markers = morphology.label(local_maxi)
>>> labels_ws = watershed(-distance, markers, mask=image)

Random walker segmentation

The random walker algorithm (skimage.segmentation.random_walker()) is similar to the Watershed, but with a more “probabilistic” approach. It is based on the idea of the diffusion of labels in the image:

>>>

>>> from skimage import segmentation
>>> # Transform markers image so that 0-valued pixels are to
>>> # be labelled, and -1-valued pixels represent background
>>> markers[~image] = -1
>>> labels_rw = segmentation.random_walker(image, markers)

Postprocessing label images

skimage provides several utility functions that can be used on label images (ie images where different discrete values identify different regions). Functions names are often self-explaining:skimage.segmentation.clear_border(),skimage.segmentation.relabel_from_one(),skimage.morphology.remove_small_objects(), etc.

Exercise

• Load the coins image from the data submodule.
• Separate the coins from the background by testing several segmentation methods: Otsu thresholding, adaptive thresholding, and watershed or random walker segmentation.
• If necessary, use a postprocessing function to improve the coins / background segmentation.

from skimage import  morphology
from skimage.morphology import watershed
from skimage.feature import peak_local_max
import matplotlib.pyplot as plt
import numpy as np

# Generate an initial image with two overlapping circles
x, y = np.indices((80, 80))
x1, y1, x2, y2 = 28, 28, 44, 52
r1, r2 = 16, 20
mask_circle1 = (x - x1) ** 2 + (y - y1) ** 2 < r1 ** 2
mask_circle2 = (x - x2) ** 2 + (y - y2) ** 2 < r2 ** 2
image = np.logical_or(mask_circle1, mask_circle2)
# Now we want to separate the two objects in image
# Generate the markers as local maxima of the distance
# to the background
from scipy import ndimage
distance = ndimage.distance_transform_edt(image)
local_maxi = peak_local_max(distance, indices=False, footprint=np.ones((3, 3)), labels=image)
markers = morphology.label(local_maxi)
labels_ws = watershed(-distance, markers, mask=image)

plt.subplot(131)
plt.imshow(image)
plt.axis('off')
plt.title('image')

plt.subplot(132)
plt.imshow(markers)
plt.axis('off')
plt.title('mark')

plt.subplot(133)
plt.imshow(labels_ws)
plt.axis('off')
plt.title('labels_ws')

plt.show()

3.3.5. Measuring regions’ properties

from skimage import measure

Example: compute the size and perimeter of the two segmented regions:

>>>

>>> properties = measure.regionprops(labels_rw)
>>> [prop.area for prop in properties]
[770, 1168]
>>> [prop.perimeter for prop in properties] 
[100.91..., 126.81...]

See also

 

for some properties, functions are available as well inscipy.ndimage.measurements with a different API (a list is returned).

Exercise (continued)

• Use the binary image of the coins and background from the previous exercise.
• Compute an image of labels for the different coins.
• Compute the size and eccentricity of all coins.

3.3.6. Data visualization and interaction

Meaningful visualizations are useful when testing a given processing pipeline.

Some image processing operations:

>>>

>>> coins = data.coins()
>>> mask = coins > filters.threshold_otsu(coins)
>>> clean_border = segmentation.clear_border(mask)

Visualize binary result:

>>>

>>> plt.figure() 
<matplotlib.figure.Figure object at 0x...>
>>> plt.imshow(clean_border, cmap='gray') 
<matplotlib.image.AxesImage object at 0x...>

Visualize contour

>>>

>>> plt.figure() 
<matplotlib.figure.Figure object at 0x...>
>>> plt.imshow(coins, cmap='gray') 
<matplotlib.image.AxesImage object at 0x...>
>>> plt.contour(clean_border, [0.5]) 
<matplotlib.contour.QuadContourSet ...>

Use skimage dedicated utility function:

>>>

>>> coins_edges = segmentation.mark_boundaries(coins, clean_border.astype(np.int))

The (experimental) scikit-image viewer

skimage.viewer = matplotlib-based canvas for displaying images + experimental Qt-based GUI-toolkit

>>>

>>> from skimage import viewer
>>> new_viewer = viewer.ImageViewer(coins) 
>>> new_viewer.show() 

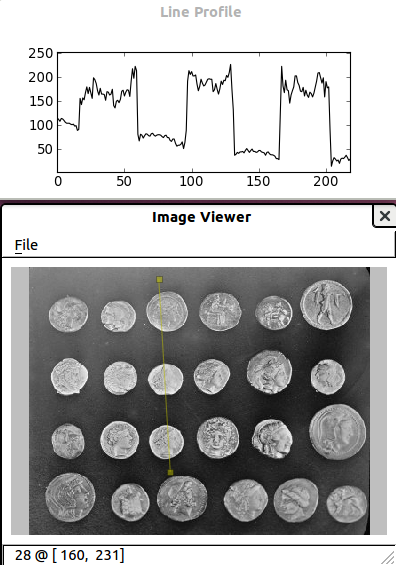
Useful for displaying pixel values.

For more interaction, plugins can be added to the viewer:

>>>

>>> new_viewer = viewer.ImageViewer(coins) 
>>> from skimage.viewer.plugins import lineprofile
>>> new_viewer += lineprofile.LineProfile() 
>>> new_viewer.show() 

3.3.7. Feature extraction for computer vision

Geometric or textural descriptor can be extracted from images in order to

• classify parts of the image (e.g. sky vs. buildings)
• match parts of different images (e.g. for object detection)
• and many other applications of Computer Vision

>>>

>>> from skimage import feature

Example: detecting corners using Harris detector

from skimage.feature import corner_harris, corner_subpix, corner_peaks
from skimage.transform import warp, AffineTransform


tform = AffineTransform(scale=(1.3, 1.1), rotation=1, shear=0.7,
                        translation=(210, 50))
image = warp(data.checkerboard(), tform.inverse, output_shape=(350, 350))

coords = corner_peaks(corner_harris(image), min_distance=5)
coords_subpix = corner_subpix(image, coords, window_size=13)

(this example is taken from the plot_corner example in scikit-image)

Points of interest such as corners can then be used to match objects in different images, as described in the plot_matching example of scikit-image.

3.3.8. Full code examples

3.3.9. Examples for the scikit-image chapter

3.3.9.1. Creating an image

How to create an image with basic NumPy commands : np.zeros, slicing…

This examples show how to create a simple checkerboard.

import numpy as np
import matplotlib.pyplot as plt

check = np.zeros((9, 9))
check[::2, 1::2] = 1
check[1::2, ::2] = 1
plt.matshow(check, cmap='gray')
plt.show()

3.3.9.2. Displaying a simple image

Load and display an image

import matplotlib.pyplot as plt
from skimage import data

camera = data.camera()


plt.figure(figsize=(4, 4))
plt.imshow(camera, cmap='gray', interpolation='nearest')
plt.axis('off')

plt.tight_layout()
plt.show()

3.3.9.3. Integers can overflow

An illustration of overflow problem arising when working with integers

import matplotlib.pyplot as plt
from skimage import data

camera = data.camera()
camera_multiply = 3 * camera

plt.figure(figsize=(8, 4))
plt.subplot(121)
plt.imshow(camera, cmap='gray', interpolation='nearest')
plt.axis('off')
plt.subplot(122)
plt.imshow(camera_multiply, cmap='gray', interpolation='nearest')
plt.axis('off')

plt.tight_layout()
plt.show()

3.3.9.4. Computing horizontal gradients with the Sobel filter

This example illustrates the use of the horizontal Sobel filter, to compute horizontal gradients.

from skimage import data
from skimage import filters
import matplotlib.pyplot as plt

text = data.text()
hsobel_text = filters.sobel_h(text)

plt.figure(figsize=(12, 3))

plt.subplot(121)
plt.imshow(text, cmap='gray', interpolation='nearest')
plt.axis('off')
plt.subplot(122)
plt.imshow(hsobel_text, cmap='spectral', interpolation='nearest')
plt.axis('off')
plt.tight_layout()
plt.show()

3.3.9.5. Equalizing the histogram of an image

Histogram equalizing makes images have a uniform histogram.

from skimage import data, exposure
import matplotlib.pyplot as plt

camera = data.camera()
camera_equalized = exposure.equalize_hist(camera)

plt.figure(figsize=(7, 3))

plt.subplot(121)
plt.imshow(camera, cmap='gray', interpolation='nearest')
plt.axis('off')
plt.subplot(122)
plt.imshow(camera_equalized, cmap='gray', interpolation='nearest')
plt.axis('off')
plt.tight_layout()
plt.show()

3.3.9.6. Segmentation contours

Visualize segmentation contours on original grayscale image.

from skimage import data, segmentation
from skimage import filters
import matplotlib.pyplot as plt
import numpy as np

coins = data.coins()
mask = coins > filters.threshold_otsu(coins)
clean_border = segmentation.clear_border(mask).astype(np.int)

coins_edges = segmentation.mark_boundaries(coins, clean_border)

plt.figure(figsize=(8, 3.5))
plt.subplot(121)
plt.imshow(clean_border, cmap='gray')
plt.axis('off')
plt.subplot(122)
plt.imshow(coins_edges)
plt.axis('off')

plt.tight_layout()
plt.show()

3.3.9.7. Otsu thresholding

This example illustrates automatic Otsu thresholding.

import matplotlib.pyplot as plt
from skimage import data
from skimage import filters
from skimage import exposure

camera = data.camera()
val = filters.threshold_otsu(camera)

hist, bins_center = exposure.histogram(camera)

plt.figure(figsize=(9, 4))
plt.subplot(131)
plt.imshow(camera, cmap='gray', interpolation='nearest')
plt.axis('off')
plt.subplot(132)
plt.imshow(camera < val, cmap='gray', interpolation='nearest')
plt.axis('off')
plt.subplot(133)
plt.plot(bins_center, hist, lw=2)
plt.axvline(val, color='k', ls='--')

plt.tight_layout()
plt.show()

3.3.9.8. Labelling connected components of an image

This example shows how to label connected components of a binary image, using the dedicated skimage.measure.label function.

from skimage import measure
from skimage import filters
import matplotlib.pyplot as plt
import numpy as np

n = 12
l = 256
np.random.seed(1)
im = np.zeros((l, l))
points = l * np.random.random((2, n ** 2))
im[(points[0]).astype(np.int), (points[1]).astype(np.int)] = 1
im = filters.gaussian_filter(im, sigma= l / (4. * n))
blobs = im > 0.7 * im.mean()

all_labels = measure.label(blobs)
blobs_labels = measure.label(blobs, background=0)

plt.figure(figsize=(9, 3.5))
plt.subplot(131)
plt.imshow(blobs, cmap='gray')
plt.axis('off')
plt.subplot(132)
plt.imshow(all_labels, cmap='spectral')
plt.axis('off')
plt.subplot(133)
plt.imshow(blobs_labels, cmap='spectral')
plt.axis('off')

plt.tight_layout()
plt.show()

3.3.9.9. Affine transform

Warping and affine transforms of images.

from matplotlib import pyplot as plt

from skimage import data
from skimage.feature import corner_harris, corner_subpix, corner_peaks
from skimage.transform import warp, AffineTransform


tform = AffineTransform(scale=(1.3, 1.1), rotation=1, shear=0.7,
                        translation=(210, 50))
image = warp(data.checkerboard(), tform.inverse, output_shape=(350, 350))

coords = corner_peaks(corner_harris(image), min_distance=5)
coords_subpix = corner_subpix(image, coords, window_size=13)

plt.gray()
plt.imshow(image, interpolation='nearest')
plt.plot(coords_subpix[:, 1], coords_subpix[:, 0], '+r', markersize=15, mew=5)
plt.plot(coords[:, 1], coords[:, 0], '.b', markersize=7)
plt.axis('off')
plt.show()

3.3.9.10. Various denoising filters

This example compares several denoising filters available in scikit-image: a Gaussian filter, a median filter, and total variation denoising.

import numpy as np
import matplotlib.pyplot as plt
from skimage import data
from skimage import filters
from skimage import restoration

coins = data.coins()
gaussian_filter_coins = filters.gaussian(coins, sigma=2)
med_filter_coins = filters.median(coins, np.ones((3, 3)))
tv_filter_coins = restoration.denoise_tv_chambolle(coins, weight=0.1)

plt.figure(figsize=(16, 4))
plt.subplot(141)
plt.imshow(coins[10:80, 300:370], cmap='gray', interpolation='nearest')
plt.axis('off')
plt.title('Image')
plt.subplot(142)
plt.imshow(gaussian_filter_coins[10:80, 300:370], cmap='gray',
           interpolation='nearest')
plt.axis('off')
plt.title('Gaussian filter')
plt.subplot(143)
plt.imshow(med_filter_coins[10:80, 300:370], cmap='gray',
           interpolation='nearest')
plt.axis('off')
plt.title('Median filter')
plt.subplot(144)
plt.imshow(tv_filter_coins[10:80, 300:370], cmap='gray',
           interpolation='nearest')
plt.axis('off')
plt.title('TV filter')
plt.show()

3.3.9.11. Watershed and random walker for segmentation

This example compares two segmentation methods in order to separate two connected disks: the watershed algorithm, and the random walker algorithm.

Both segmentation methods require seeds, that are pixels belonging unambigusouly to a reagion. Here, local maxima of the distance map to the background are used as seeds.

import numpy as np
from skimage.morphology import watershed
from skimage.feature import peak_local_max
from skimage import measure
from skimage.segmentation import random_walker
import matplotlib.pyplot as plt
from scipy import ndimage

# Generate an initial image with two overlapping circles
x, y = np.indices((80, 80))
x1, y1, x2, y2 = 28, 28, 44, 52
r1, r2 = 16, 20
mask_circle1 = (x - x1) ** 2 + (y - y1) ** 2 < r1 ** 2
mask_circle2 = (x - x2) ** 2 + (y - y2) ** 2 < r2 ** 2
image = np.logical_or(mask_circle1, mask_circle2)
# Now we want to separate the two objects in image
# Generate the markers as local maxima of the distance
# to the background
distance = ndimage.distance_transform_edt(image)
local_maxi = peak_local_max(
    distance, indices=False, footprint=np.ones((3, 3)), labels=image)
markers = measure.label(local_maxi)
labels_ws = watershed(-distance, markers, mask=image)

markers[~image] = -1
labels_rw = random_walker(image, markers)

plt.figure(figsize=(12, 3.5))
plt.subplot(141)
plt.imshow(image, cmap='gray', interpolation='nearest')
plt.axis('off')
plt.title('image')
plt.subplot(142)
plt.imshow(-distance, interpolation='nearest')
plt.axis('off')
plt.title('distance map')
plt.subplot(143)
plt.imshow(labels_ws, cmap='spectral', interpolation='nearest')
plt.axis('off')
plt.title('watershed segmentation')
plt.subplot(144)
plt.imshow(labels_rw, cmap='spectral', interpolation='nearest')
plt.axis('off')
plt.title('random walker segmentation')

plt.tight_layout()
plt.show()