数据结构与算法（python）：图(Graph)的基本概念及应用

最新推荐文章于 2025-02-26 16:20:48 发布

番茄大人

最新推荐文章于 2025-02-26 16:20:48 发布

阅读量1.4w

点赞数 9

分类专栏： Python数据结构文章标签： python 算法

本文链接：https://blog.csdn.net/wd9ljs18/article/details/112191078

版权

Python数据结构专栏收录该内容

19 篇文章

订阅专栏

参考自 MOOC数据结构与算法Python版
本章代码: https://github.com/HuiFang-hub/-/tree/main.

一、图Graph的概念

图Graph是比树更为一般的结构，也是由节点和边构成
实际上树是一种具有特殊性质的图
图可以用来表示现实世界中很多事物
道路交通系统、航班线路、互联网连接、或者是大学中课程的先修次序

一旦我们对图相关问题进行了准确的描述，就可以采用处理图的标准算法来解决那些
看起来很艰深的问题

1.1 互联网

互联网是一张百亿个信息点的巨型网络
提供内容的Web站点已突破10亿个
由超链接相互连接的网页更是不计其数
Google每天处理的数据量约10PB
在天文数字规模的网络面前人脑已经无法处理

1.2 社交网络：六度分隔理论

世界上任何两个人之间通过最多6个人即可建立联系
互联网社交网络的兴起将每个人联系到一起
在社会中有20%擅长交往的人，建立了80%的连接
区别于随机网络，保证了六度分隔的成立引出了无尺度网络的研究

二、术语表

顶点 Vertex（也“节点node”）
是图的基本组成部分，定点具有名称标识key，也可以携带数据项payload。
边 Edge（也称“弧Arc”）
作为2个顶点之间关系的表示，边连接两个顶点；边可以是有向的或者无向的，相应的图称做“有向图”和“无向图”。
权重 Weight
为了表达从一个顶点到另一个顶点的“代价”，可以给边赋权；例如公交网络中两个站点之间的“距离”、“通行时间”和“票价”都可以作为权重。
路径Path
图中的路径，是由边依次链接起来的顶点序列；无权路径的长度为边的数量；带权路径的长度为所有边权重的和；如下图的一条路径(v3,v4,v0,v1)
圈Cycle
圈是首尾顶点相同的路径，如下图中（V5,V2,V3,V5）
如果有向图中不存在任何圈，则称为“有向无圈图 directed acyclic graph：DAG”
如果一个问题能表示成DAG，就可以用图算法很好地解决。

三、图抽象数据类型：ADT Graph

3.1 定义

函数	含义
Graph()	创建一个空图
addVertex(vert)	将顶点vert加入图中
addEdge(fromVert, toVert)	添加有向边
addEdge(fromVert, toVert, weight)	添加带权的有向边
getVertex(vKey)	查找名称为vKey的顶点
getVertices()	返回图中所有顶点列表
in	按照vert in graph的语句形式，返回顶点是否存在图中True/False

3.2 ADT Graph的实现方法

两种方法各有优劣，需要在不同应用中加以选择

邻接矩阵adjacency matrix
邻接表adjacency list

3.2.1 邻接矩阵Adjacency Matrix

矩阵的每行和每列都代表图中的顶点，如果两个顶点之间有边相连，设定行列值

无权边则将矩阵分量标注为1，或者0
带权边则将权重保存为矩阵分量值

例如下面的带权图：
在这里插入图片描述

邻接矩阵顶实现法的优点是简单，可以很容易得到顶点是如何相连
但如果图中的边数很少则效率低下，成为“稀疏sparse”矩阵，而大多数问题所对应的图都是稀疏的，边远远少于|V|²这个量级，从而出现邻接列表。

3.2.2 邻接列表Adjacency List

邻接列表可以成为稀疏图的更高效实现方案
维护一个包含所有顶点的主列表（master list）。主列表中的每个顶点，再关联一个与自身由边链接的所有顶点的列表。
邻接列表法的寻出空间紧凑高效
很容易获得顶点所连接的所有顶点以及边的信息

例如上面的图转为邻接列表，与V0有关的有V1和V5，权重分别是5和2：
在这里插入图片描述

四、ADT Graph的实现：实例

4.1 Vertex类

下面展示了 Vertex 类的代码，包含了顶点信息，以及顶点连接边信息

class Vertex:
    def __init__(self,key):
        self.id = key
        self.connectedTo = {}
	#从这个顶点添加一个连接到另一个
    def addNeighbor(self,nbr,weight=0):  #nbr是顶点对象的key
        self.connectedTo[nbr] = weight
	#顶点数据字符串化，方便打印
    def __str__(self):
        return str(self.id) + ' connectedTo: ' + str([x.id for x in self.connectedTo])
	#返回邻接表中的所有顶点
    def getConnections(self):
        return self.connectedTo.keys()
	#返回key
    def getId(self):
        return self.id
	#返回顶点边的权重。
    def getWeight(self,nbr):
        return self.connectedTo[nbr]

4.2 Graph 类

下面展示了 Graph 类的代码，包含将顶点名称映射到顶点对象的字典。Graph 还提供了将顶点添加到图并将一个顶点连接到另一个顶点的方法。getVertices方法返回图中所有顶点的名称。此外，我们实现了__iter__ 方法，以便轻松地遍历特定图中的所有顶点对象。这两种方法允许通过名称或对象本身在图形中的顶点上进行迭代。

class Graph:
    def __init__(self):
        self.vertList = {}
        self.numVertices = 0
	#新加顶点
    def addVertex(self,key):
        self.numVertices = self.numVertices + 1
        newVertex = Vertex(key)
        self.vertList[key] = newVertex
        return newVertex
	#通过key查找顶点
    def getVertex(self,n):
        if n in self.vertList:
            return self.vertList[n]
        else:
            return None

    def __contains__(self,n):
        return n in self.vertList
   
    def addEdge(self,f,t,cost=0):
        if f not in self.vertList: #不存在的顶点先添加
            nv = self.addVertex(f)
        if t not in self.vertList:
            nv = self.addVertex(t)
        self.vertList[f].addNeighbor(self.vertList[t], cost)

    def getVertices(self):
        return self.vertList.keys()

    def __iter__(self):
        return iter(self.vertList.values())

g = Graph()
for i in range(6):
    g.addVertex(i)
g.addEdge(0,1,5)
g.addEdge(0,5,2)
g.addEdge(1,2,4)
g.addEdge(2,3,9)
g.addEdge(3,4,7)
g.addEdge(3,5,3)
g.addEdge(4,0,1)
g.addEdge(5,4,8)
g.addEdge(5,2,1)
for v in g:  #遍历输出
    for w in v.getConnections():
        print("( %s , %s )" % (v.getId(), w.getId()))

Out: 
{0: <__main__.Vertex at 0x2459cdf65f8>,
 1: <__main__.Vertex at 0x2459cdf6630>,
 2: <__main__.Vertex at 0x2459cdf6668>,
 3: <__main__.Vertex at 0x2459cdf66a0>,
 4: <__main__.Vertex at 0x2459cdf66d8>,
 5: <__main__.Vertex at 0x2459cdf6710>}
( 0 , 1 )
( 0 , 5 )
( 1 , 2 )
( 2 , 3 )
( 3 , 4 )
( 3 , 5 )
( 4 , 0 )
( 5 , 4 )
( 5 , 2 )

五、图的应用

5.1 词梯问题

由 “ 爱丽丝漫游奇境 ” 的作者 LewisCarroll在1878年所发明的单词游戏。

从一个单词演变到另一个单词，其中的过程可以经过多个中间单词，要求是相邻两个单词之间差异只能是1个字母，如FOOL变SAGE：
FOOL >> POOL >> POLL >> POLE >> PALE>> SALE >> SAGE

我们的目标是找到最短的单词变换序列，采用图来解决这个问题的步骤如下：

将可能的单词之间的演变关系表达为图
采用“广度优先搜索 BFS”，来搜寻从开始单词到结束单词之间的所有有效路径
选择其中最快到达目标单词的路径

5.1.1 构建单词关系图

首先是如何将大量的单词集放到图中：将单词作为顶点的标识Key，如果两个单词之间仅相差1个字母，就在它们之间设一条边
下图是从FOOL到SAGE的词梯解，所用的图是无向图，边没有权重
在这里插入图片描述
单词关系图可以通过不同的算法来构建（以4个字母的单词表为例）

首先是将所有单词作为顶点加入图中，再设法建立顶点之间的边
建立边的最直接算法，是对每个顶点（单词），与其它所有单词进行比较，如果相差仅1个字母，则建立一条边
时间复杂度是O(n^2)，对于所有4个字母的5110个单词，需要超过2600万次比较
改进的算法是创建大量的桶，每个桶可以存放若干单词
桶标记是去掉1个字母，通配符“_”占空的单词
所有单词就位后，再在同一个桶的单词之间建立边即可

在这里插入图片描述

5.1.2 采用字典建立桶

def buildGraph(wordfile):
    d = {}
    g = Graph()
    wfile = open(wordfile,'r')
    for line in wfile:
        word = line[:-1]
        for i in range(len(word)):
            bucket = word[:i] + '_' + word[i+1:]
            if bucket in d:
                d[bucket].append(word)
            else:
                d[bucket] = [word]
        #同一个桶的单词建立边
        for bucket in d.keys():
            for word1 in d[bucket]:
                for word2 in d[bucket]:
                    if word1 != word2:
                        g.addEdge(word1, word2)
        return g

注意，如果采用邻接矩阵表示这个单词关系图，则需要2,600万个矩阵单元，单词关系图是一个非常稀疏的图

5.2 拓扑排序（Topological Sort）

很多问题都可转化为图，利用图算法解决，例如早餐吃薄煎饼的过程，以动作为顶点，以先后次序为有向边。（有先后次序和依赖关系）
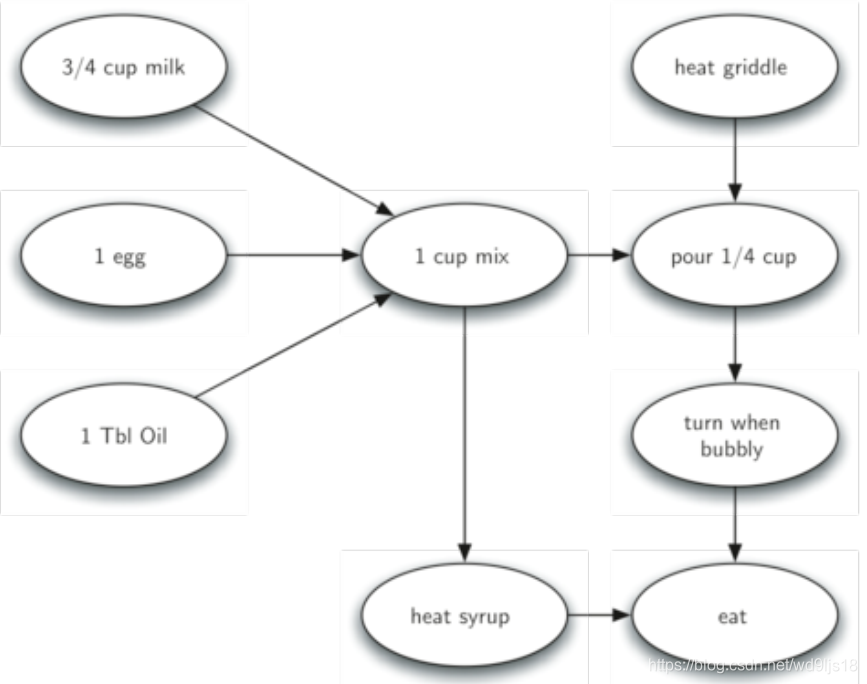在这里插入图片描述从工作流程图得到工作次序排列的算法，称为“拓扑排序”

拓扑排序处理一个有向无圈图（DAG），输出顶点的线性序列：使得两个顶点v,w，如果G中有(v,w)边，在线性序列中v就出现在w之前。

拓扑排序广泛应用在依赖事件的排期上，还可以用在项目管理、数据库查询优化和矩阵乘法的次序优化上。拓扑排序可以采用DFS很好地实现：

将工作流程建立为图，工作项是节点，依赖关系是有向边
工作流程图一定是个DAG图，否则有循环依赖
对DAG图调用DFS算法，以得到每个顶点的“结束时间”，按照每个顶点的“结束时间”从大到小排序
输出这个次序下的顶点列表

5.3 强连通分支

我们关注一下互联网相关的非常巨大图：

由主机通过网线（或无线）连接而形成的图；
以及由网页通过超链接连接而形成的图。

先看网页形成的图
以网页（URI作为id）为顶点，网页内包含的超链接作为边，可以转换为一个有向图。
图中包含了许多路德学院其它系的网站，包含了一些爱荷华其它大学学院的网站，还包含了一些人文学院的网站。

我们可以猜想， Web的底层结构可能存在某些同类网站的聚集

在图中发现高度聚集节点群的算法，即寻找“强连通分支Strongly Connected Components”算法

强连通分支，定义为图G的一个子集C：C中的任意两个顶点v,w之间都有路径来回，即(v,w)(w,v)都是C的路径，而且C是具有这样性质的最大子集

下图是具有3个强连通分支的9顶点有向图，一旦找到强连通分支，可以据此对图的顶点进行分类，并对图进行化简（9个顶点变为3个顶点，相当于聚类）
在这里插入图片描述

5.3.1 强连通分支算法：转置概念

在用深度优先搜索来发现强连通分支之前，先熟悉一个概念： Transposition转置
一个有向图G的转置GT，定义为将图G的所有边的顶点交换次序，如将(v,w)转换为(w,v)。可以观察到图和转置图在强连通分支的数量和划分上，是相同的
下图互为转置，即
在这里插入图片描述

5.3.2 强连通分支算法： Kosaraju算法思路

首先，对图G调用DFS算法，为每个顶点计算“结束时间”；
然后，将图G进行转置，得到 $G^T$ ；
再对 $G^T$ 调用DFS算法，但在dfs函数中，对每个顶点的搜索循环里，要以顶点的“结束时间”倒序的顺序来搜索
最后，深度优先森林中的每一棵树就是一个强连通分支

5.3.3 Kosaraju算法实例

第一趟DFS
在这里插入图片描述
转置后第二趟DFS, 取结束时间最大的第一个开始
结果形成三个强连通分支：

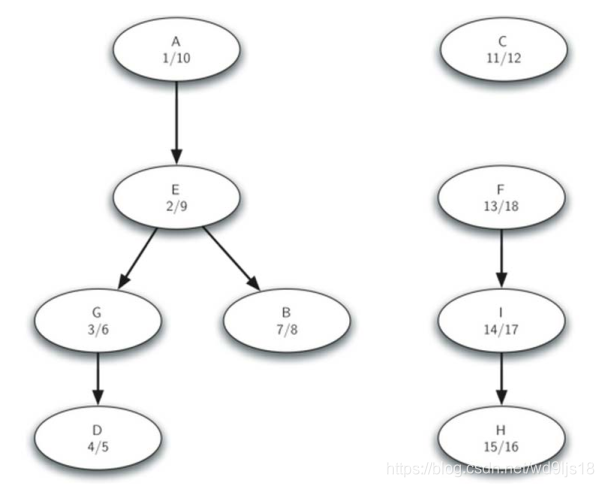
Kosaraju算法最好理解，但是效率最差，因此另外的常用强连通分支算法有：

Tarjan算法
Gabow算法，对Tarjan的改进

参考阅读：https://baike.baidu.com/item/tarjan算法.

5.4 最短路径问题

5.4.1 介绍

当我们通过网络浏览网页、发送电子邮件、 QQ消息传输的时候，数据会在联网设备之间流动。
所以我们可以将互联网路由器体系表示为
一个带权边的图：

路由器作为顶点，路由器之间网络连接作为边
权重可以包括网络连接的速度、网络负载程度、分时段优先级等影响因素
作为一个抽象，我们把所有影响因素合成为单一的权重
解决信息在路由器网络中选择传播速度最快路径的问题，就转变为在带权图上最短路径的问题。
与广度优先搜索BFS算法解决的词梯问题相似，只是在边上增加了权重。

5.4.2 Dijkstra算法

解决带权最短路径问题的经典算法是以发明者命名的“Dijkstra算法”（ /ˈdɛɪkstra）
这是一个迭代算法，得出从一个顶点到其余所有顶点的最短路径，很接近于广度优先搜索算法BFS的结果
具体实现上，在顶点Vertex类中的成员dist用于记录从开始顶点到本顶点的最短带权路径长度（权重之和），算法对图中的每个顶点迭代一次
步骤：

顶点的访问次序由一个优先队列来控制，队列中作为优先级的是顶点的dist属性。
最初，只有开始顶点dist设为0，而其他所有顶点dist设为sys.maxsize（最大整数），全部加入优先队列；
随着队列中每个最低dist顶点率先出队；
并计算它与邻接顶点的权重，会引起其它顶点dist的减小和修改，引起堆重排；
并据更新后的dist优先级再依次出队。

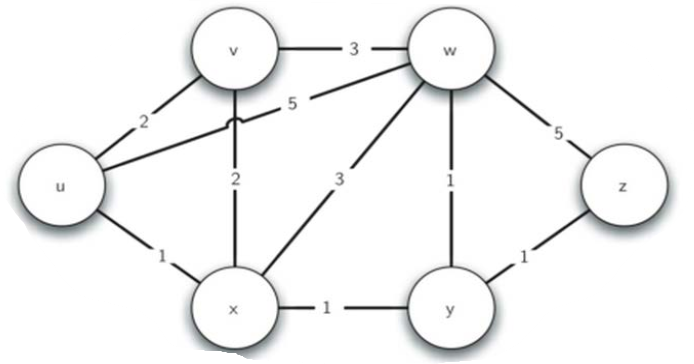
以下图为例：

设u为开始顶点，计算与u相连的其他顶点的权重，并将u出队。
更新v，x的权重，将较小的x（d=1）出队
计算与x相连的v，w，y的权重，v:1+2=3 > 2，因此不更新权重，其余的更新。将最小的v出队
同时y(d=2)也出队，计算与之相连的w,z，并更新w,z
将w,z出队

form pythonds.graphs import Graph,PriorityQueue,Vertex
def dijkstra(aGraph, start):
    pq = PriorityQueue()
    start.setDistance(0)#开始点的距离设为0
    pq.buildHeap([(v.getDistance(), v) for v in aGraph]) #对所有顶点建堆，形成优先队列
    while not pq.isEmpty():
        currentVert = pq.delMin() #优先队列出队
        for nextVert in currentVert.getConnections():
            newDist = currentVert.getDistance() + currentVert.getWeight(nextVert)
            if newDist < nextVert.getDistance():#修改出队顶点所邻接顶点的dist，并逐个顶点的dist，并逐个
                nextVert.setDistance(newDist)
                nextVert.setPred(currentVert)
                pq.decreaseKey(nextVert, newDist)

需要注意的是， Dijkstra算法只能处理大于0的权重，如果图中出现负数权重，则算法会陷入无限循环。
虽然Dijkstra算法完美解决了带权图的最短路径问题，但实际上Internet的路由器中采用的是其它算法，其中最重要的原因是， Dijkstra算法需要具备整个图的数据，但对于Internet的路由器来说，显然无法将整个Internet所有路由器及其连接信息保存在本地，路由器的选径算法（或“路由算法”）对于互联网极其重要，有兴趣可以进一步参考“距离向量路由算法“。

5.4.3 Dijkstra算法分析

首先，将所有顶点加入优先队列并建堆，时间复杂度为O(|V|)
其次，每个顶点仅出队1次，每次delMin 花费O(log|V|)，一共就是O(|V|log|V|)
另外，每个边关联到的顶点会做一次decreaseKey操作（O(log|V|))，一共是O(|E|log|V|)

上面三个加在一起，数量级就是 $O ((∣ V ∣ + ∣ E ∣) l o g ∣ V ∣)$

5.5 最小生成树

本算法涉及到在互联网中网游设计者和网络收音机所面临的问题：信息广播问题

信息广播问题最简单的解法是：由广播源维护一个收听者的列表，将每条消息向每个收听者发送一次
信息广播问题的暴力解法，是将每条消息在路由器间散布出去，如果没有任何限制，这个方法将造成网络洪水灾难。
洪水解法一般会给每条消息附加一个生命值（TTL:Time To Live），初始设置为从消息源到最远的收听者的距离；每个路由器收到一条消息，如果其TTL值大于0，则将TTL减少1，再转发出去，TTL的设置防止了灾难发生，但这种洪水解法显然比前述的单播方法所产生的流量还要大。
信息广播问题的最优解法，依赖于路由器关系图上选取具有最小权重的生成树（minimum weight spanning tree）
生成树：拥有图中所有的顶点和最少数量的边，以保持连通的子图。

图G(V,E)的最小生成树T，定义为包含所有顶点V，以及E的无圈子集，并且边权重之和最小。
图为一个最小生成树，这样信息广播就只需要从A开始，沿着树的路径层次向下传播就可以达到每个路由器只需要处理1次消息，同时总费用最小。

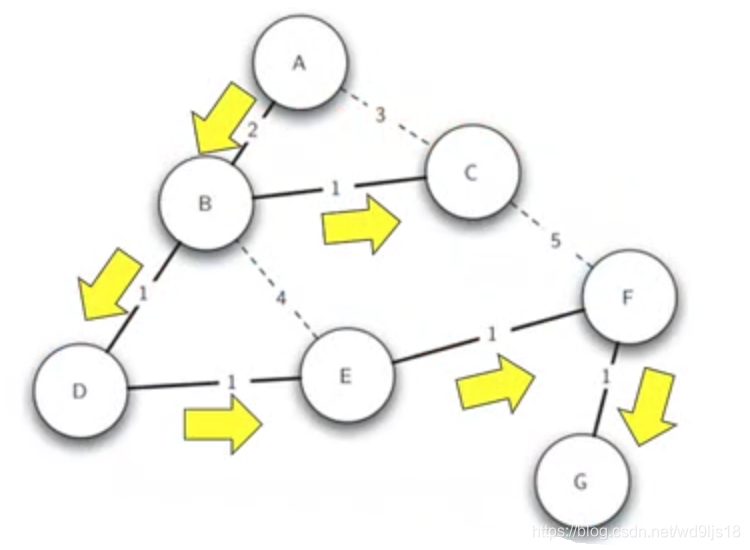
在这里插入图片描述

5.5.1 Prim算法

解决最小生成树问题的Prim算法，属于“贪心算法”，即每步都沿着最小权重的边向前搜索。
构造最小生成树的思路很简单，如果T还不是生成树，则反复做：

找到一条最小权重的可以安全添加的边，将边添加到树T
“可以安全添加”的边，定义为一端顶点在树中，另一端不在树中的边，以便保持树的无圈特性

from pq import PriorityQueue, Graph, Vertex
# 最小生成树prim算法
# G - 无向赋权图
# start - 开始节点
# 返回从开始节点创建最小生成树
def prim(G, start):
    pq = PriorityQueue()  # 创建优先队列
    start.setDistance(0)  # 起点最小权重代价设置为0，其它节点最小权重代价默认maxsize
    # 将节点排入优先队列，start在最前面
    pq.buildHeap([(v.getDistance(), v) for v in G])
    while not pq.isEmpty():
        # 取距离*已有树*最小权重代价的节点出队列，作为当前节点
        # 当前节点已解出最小生成树的前驱pred和对应最小权重代价dist
        currentVert = pq.delMin()
        # 遍历节点的所有邻接节点
        for nextVert in currentVert.getConnections():
            # 从当前节点出发，逐个检验到邻接节点的权重
            newCost = currentVert.getWeight(nextVert)
            # 如果邻接节点是"安全边"，并且小于邻接节点原有最小权重代价dist，就更新邻接节点
            if nextVert in pq and newCost < nextVert.getDistance():
                # 更新最小权重代价dist
                nextVert.setPred(currentVert)
                # 更新返回路径
                nextVert.setDistance(newCost)
                # 更新优先队列
                pq.decreaseKey(nextVert, newCost)


G = Graph()
ndedge = [('A', 'B', 2), ('A', 'C', 3), ('B', 'C', 1),
          ('B', 'D', 1), ('B', 'E', 4), ('C', 'F', 5),
          ('D', 'E', 1), ('E', 'F', 1), ('F', 'G', 1)]
for nd in ndedge:
    G.addEdge(nd[0], nd[1], nd[2])
    G.addEdge(nd[1], nd[0], nd[2])
start = G.getVertex('A')
prim(G, start)
print(G)

G = Graph()
ndedge = [('v1', 'v2', 6), ('v1', 'v3', 1), ('v1', 'v4', 5),
          ('v2', 'v3', 5), ('v3', 'v4', 5), ('v2', 'v5', 3),
          ('v3', 'v5', 6), ('v3', 'v6', 4), ('v4', 'v6', 2),
          ('v5', 'v6', 6)]
for nd in ndedge:
    G.addEdge(nd[0], nd[1], nd[2])
    G.addEdge(nd[1], nd[0], nd[2])
start = G.getVertex('v1')
prim(G, start)
print(G)

pq.py

import sys


class Graph:
    def __init__(self):
        self.vertices = {}
        self.numVertices = 0

    def addVertex(self, key):
        self.numVertices = self.numVertices + 1
        newVertex = Vertex(key)
        self.vertices[key] = newVertex
        return newVertex

    def getVertex(self, n):
        if n in self.vertices:
            return self.vertices[n]
        else:
            return None

    def __contains__(self, n):
        return n in self.vertices

    def addEdge(self, f, t, cost=0):
        if f not in self.vertices:
            nv = self.addVertex(f)
        if t not in self.vertices:
            nv = self.addVertex(t)
        self.vertices[f].addNeighbor(self.vertices[t], cost)

    def getVertices(self):
        return list(self.vertices.keys())

    def __iter__(self):
        return iter(self.vertices.values())

    def __str__(self):
        s = ""
        for v in self:
            s += f"[{v.id},{v.dist},{v.pred.id if v.pred else None}] "
        return s


class Vertex:
    def __init__(self, num):
        self.id = num
        self.connectedTo = {}
        self.color = 'white'
        self.dist = sys.maxsize
        self.pred = None
        self.disc = 0
        self.fin = 0

    # def __lt__(self,o):
    #     return self.id < o.id

    def addNeighbor(self, nbr, weight=0):
        self.connectedTo[nbr] = weight

    def setColor(self, color):
        self.color = color

    def setDistance(self, d):
        self.dist = d

    def setPred(self, p):
        self.pred = p

    def setDiscovery(self, dtime):
        self.disc = dtime

    def setFinish(self, ftime):
        self.fin = ftime

    def getFinish(self):
        return self.fin

    def getDiscovery(self):
        return self.disc

    def getPred(self):
        return self.pred

    def getDistance(self):
        return self.dist

    def getColor(self):
        return self.color

    def getConnections(self):
        return self.connectedTo.keys()

    def getWeight(self, nbr):
        return self.connectedTo[nbr]

    def __str__(self):
        return str(self.id) + ":color " + self.color + ":disc " + str(self.disc) + ":fin " + str(
            self.fin) + ":dist " + str(self.dist) + ":pred \n\t[" + str(self.pred) + "]\n"

    def __repr__(self):
        return str(self.id)

    def getId(self):
        return self.id


class PriorityQueue:
    def __init__(self):
        self.heapArray = [(0, 0)]
        self.currentSize = 0

    def buildHeap(self, alist):
        self.currentSize = len(alist)
        self.heapArray = [(0, 0)]
        for i in alist:
            self.heapArray.append(i)
        i = len(alist) // 2
        while (i > 0):
            self.percDown(i)
            i = i - 1

    def percDown(self, i):
        while (i * 2) <= self.currentSize:
            mc = self.minChild(i)
            if self.heapArray[i][0] > self.heapArray[mc][0]:
                tmp = self.heapArray[i]
                self.heapArray[i] = self.heapArray[mc]
                self.heapArray[mc] = tmp
            i = mc

    def minChild(self, i):
        if i * 2 > self.currentSize:
            return -1
        else:
            if i * 2 + 1 > self.currentSize:
                return i * 2
            else:
                if self.heapArray[i * 2][0] < self.heapArray[i * 2 + 1][0]:
                    return i * 2
                else:
                    return i * 2 + 1

    def percUp(self, i):
        while i // 2 > 0:
            if self.heapArray[i][0] < self.heapArray[i // 2][0]:
                tmp = self.heapArray[i // 2]
                self.heapArray[i // 2] = self.heapArray[i]
                self.heapArray[i] = tmp
            i = i // 2

    def add(self, k):
        self.heapArray.append(k)
        self.currentSize = self.currentSize + 1
        self.percUp(self.currentSize)

    def delMin(self):
        retval = self.heapArray[1][1]
        self.heapArray[1] = self.heapArray[self.currentSize]
        self.currentSize = self.currentSize - 1
        self.heapArray.pop()
        self.percDown(1)
        return retval

    def isEmpty(self):
        if self.currentSize == 0:
            return True
        else:
            return False

    def decreaseKey(self, val, amt):
        # this is a little wierd, but we need to find the heap thing to decrease by
        # looking at its value
        done = False
        i = 1
        myKey = 0
        while not done and i <= self.currentSize:
            if self.heapArray[i][1] == val:
                done = True
                myKey = i
            else:
                i = i + 1
        if myKey > 0:
            self.heapArray[myKey] = (amt, self.heapArray[myKey][1])
            self.percUp(myKey)

    def __contains__(self, vtx):
        for pair in self.heapArray:
            if pair[1] == vtx:
                return True
        return False

    def __str__(self):
        return str(self.heapArray)