排序算法系列之希尔排序

算法排序之希尔排序

希尔排序 ，也称 递减增量排序算法 ，是插入排序 的一种高速而稳定的改进版本。  

基本思想

   先取一个小于n的整数d₁作为第一个增量，把文件的全部记录分成d₁个组。所有距离为d_l的倍数的记录放在同一个组中。先在各组内进行直接插人排序；然后，取第二个增量d₂<d₁重复上述的分组和排序，直至所取的增量d_t=1(d_t<d_t-l<…<d₂<d₁)，即所有记录放在同一组中进行直接插入排序为止。

希尔排序的时间性能优于直接插入排序的原因：
　　①当文件初态基本有序时直接插入排序所需的比较和移动次数均较少。
　　②当n值较小时，n和n²的差别也较小，即直接插入排序的最好时间复杂度O(n)和最坏时间复杂度0(n²)差别不大。
　　③在希尔排序开始时增量较大，分组较多，每组的记录数目少，故各组内直接插入较快，后来增量d_i逐渐缩小，分组数逐渐减少，而各组的记录数目逐渐增多，但由于已经按d_i-1作为距离排过序，使文件较接近于有序状态，所以新的一趟排序过程也较快。
    　因此，希尔排序在效率上较直接插人排序有较大的改进。

步长选择

Donald Shell 最初建议步长选择为并且对步长取半直到步长达到 1。虽然这样取可以比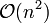类的算法（插入排序）更好，但这样仍然有减少平均时间和最差时间的余地。 可能希尔排序最重要的地方在于当用较小步长排序后，以前用的较大步长仍然是有序的。比如，如果一个数列以步长5进行了排序然后再以步长3进行排序，那么该数列不仅是以步长3有序，而且是以步长5有序。如果不是这样，那么算法在迭代过程中会打乱以前的顺序，那就不会以如此短的时间完成排序了。

步长串行	最坏情况下复杂度

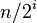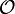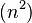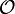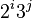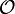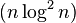已知的最好步长串行是由Sedgewick提出的 (1, 5, 19, 41, 109,...)，该串行的项来自 9 * 4^i - 9 * 2^i + 1 和 4^i - 3 * 2^i + 1 这两个算式.这项研究也表明“比较在希尔排序中是最主要的操作，而不是交换。”用这样步长串行的希尔排序比插入排序和堆排序都要快，甚至在小数组中比快速排序还快，但是在涉及大量数据时希尔排序还是比快速排序慢。

另一个在大数组中表现优异的步长串行是(斐波那契数列除去0和1将剩余的数以黄金分区比的两倍的幂进行运算得到的数列)：（1, 9, 34, 182, 836, 4025, 19001, 90358, 428481, 2034035, 9651787, 45806244, 217378076, 1031612713, …）

希尔排序动画模拟以及动态图演示

动画演示：

假设待排序文件有10个记录，其关键字分别是： 49，38，65，97，76，13，27，49，55，04。
增量序列的取值依次为： 5，3，1
排序过程如【动画模拟演示】

动态图：

 

伪码实现

input: an array a of length n with array elements numbered 0 to n − 1
inc ← round(n/2)
while inc > 0 do:    
    for i = inc .. n − 1 do:        
        temp ← a[i]        
        j ← i        
        while j ≥ inc and a[j − inc] > temp do:            
            a[j] ← a[j − inc]            
            j ← j − inc        
        a[j] ← temp    
    inc ← round(inc / 2.2)

算法C语言实现

/**
 * 希尔排序是按照不同步长对元素进行插入排序，当刚开始元素很无序的时候，步长
 * 最大，所以插入排序的元素个数很少，速度很快；当元素基本有序了,步长很小,插
 * 入排序对于有序的序列效率很高。所以，希尔排序的时间复杂度会比o(n^2)好一些!
 * 希尔排序时间复杂度为O(nlog(n)) ~ O(n ^ 2)
 */

#include <stdio.h>

void shell_sort(int array[], int n)
{
    // increment为步长
    int tmp, i, j, increment;

    for(increment = n / 2; increment > 0; increment /= 2)
    {
        //下面为插入排序，最坏时间复杂度为O（n^2）！
        for(i = increment; i < n; ++i)
        {
            tmp = array[i];

            for(j = i; j > 0 && tmp < array[j - increment]; j -= increment)
            {
                array[j] = array[j - increment];
            }
            array[j] = tmp;
        }
    }
}

测试main函数

int main()
{
    int array[] = {34，25，56，1，-1，-45};
    shell_sort(array, 6);
    for(int i = 0; i < 6; ++i)
        printf("%d ", array[i]);

    return 0;

}