查找算法（基于二叉排序树的查找）

1.二叉排序树的定义与描述
二叉排序树又称为二叉查找树，它是一种特殊的二叉树。
定义：二叉排序树是一颗空树或者是具有一下性质的二叉树。
1）若它的左子树非空，则左子树上所有的结点值均小于根结点的值。
2）若它的右子树非空，则右子树上所有的结点的值均大于（或等于）根结点的值。
3）它的左右子树也分别是二叉排序树。

2.数据结构

typedef struct  node
{
    KeyType  key ; /*关键字的值*/
    struct node  *lchild,*rchild;/*左右指针*/
}BSTNode, *BSTree;

3.二叉排序树的创建
可以将树结点逐个插入到二叉排序树（一开始可以是一颗空树）中，只要保证插入后，依然满足二叉排序树的特点，就可以创建一个二叉排序树。
设树结点的关键字值为key
算法思想：
1）若二叉排序树是空树，则将key结点成为二叉排序树的根结点。
2）若二叉排序树非空树，则将key与二叉排序树的根进行比较：
a.如果key的值等于根结点的值，则停止插入。
b.如果key的值小于根结点的值，则将key所在结点插入左子树。
c.如果key的值大于根结点的值，则将key所在结点插入右子树。
算法实现:

void InsertBST(BSTree *bst, KeyType key)
/*若在二叉排序树中不存在关键字等于key的元素，插入该元素*/
{ 
    BSTree s;
    if (*bst == NULL)/*递归结束条件*/
    {
        s=(BSTree)malloc(sizeof(BSTNode));/*申请新的结点s*/
        s-> key=key;
        s->lchild=NULL; 
        s->rchild=NULL;
        *bst=s;
    }
    else {
        if (key < (*bst)->key)
            InsertBST(&((*bst)->lchild), key);/*将s插入左子树*/
        else 
            if (key > (*bst)->key)
                InsertBST(&((*bst)->rchild), key); /*将s插入右子树*/
    }
}

4.二叉排序树的查找
因为二叉排序树是可以看作是一个有序表，所以其查找过程和折半查找类似。
算法思想：
首先将待查关键字key与根节点关键字t进行比较：
a.如果key = t, 则返回根节点指针。
b.如果key < t,则进一步查找左子书。
c.如果key > t,则进一步查找右子树。
1）递归算法实现：

/*在根指针bst所指二叉排序树中，递归查找某关键字等于key的元素，若查找成功，返回指向该元素结点指针，否则返回空指*/
BSTree  SearchBST(BSTree bst, KeyType key) {
    if (!bst) 
        return NULL;
    else 
        if (bst->key == key)
            return bst;/ *查找成功* /
        else {
            if (bst->key > key)
                return SearchBST(bst->lchild, key); /*在左子树继续查找*/
            else 
                return SearchBST(bst->rchild, key); /*在右子树继续查找*/
    }
}

2）非递归实现

BSTree  SearchBST(BSTree bst, KeyType key)
/*在根指针bst所指二叉排序树bst上，查找关键字等于key的结点，若查找成功，返回指向该元素结点指针，否则返回空指针*/
{ 
    BSTree q;
    q=bst;
    while(q)
    {
        if (q->key == key) 
            return q;  /*查找成功*/
        if (q->key > key)  
            q=q->lchild;  /*在左子树中查找*/
        else  
            q=q->rchild;  /*在右子树中查找*/
    }
    return NULL; /*查找失败*/
}

完整代码描述：

#include <stdio.h>
#include <stdlib.h>

#define ENDKEY 0

typedef int KeyType;

typedef struct  node
{
    KeyType  key ; /*关键字的值*/
    struct node  *lchild,*rchild;/*左右指针*/
}BSTNode, *BSTree;

void InsertBST(BSTree *bst, KeyType key)
/*若在二叉排序树中不存在关键字等于key的元素，插入该元素*/
{ 
    BSTree s;
    if (*bst == NULL)/*递归结束条件*/
    {
        s=(BSTree)malloc(sizeof(BSTNode));/*申请新的结点s*/
        s-> key=key;
        s->lchild=NULL; 
        s->rchild=NULL;
        *bst=s;
    }
    else 
        if (key < (*bst)->key)
            InsertBST(&((*bst)->lchild), key);/*将s插入左子树*/
        else 
            if (key > (*bst)->key)
                InsertBST(&((*bst)->rchild), key); /*将s插入右子树*/
}

void  CreateBST(BSTree  *bst)
/*从键盘输入元素的值，创建相应的二叉排序树*/
{ 
    KeyType key;
    *bst=NULL;
    scanf("%d", &key);
    while (key!=ENDKEY)   /*ENDKEY为自定义常量*/
    {
        InsertBST(bst, key);
        scanf("%d", &key);
    }
}

void  PreOrder(BSTree root) 
/*先序遍历二叉树, root为指向二叉树根结点的指针*/
{
    if (root!=NULL)
    {
        printf("%d  ",root->key);  /*输出结点*/
        PreOrder(root->lchild);  /*先序遍历左子树*/
        PreOrder(root->rchild);  /*先序遍历右子树*/
    }
}

/*
BSTree  SearchBST(BSTree bst, KeyType key)
/ *在根指针bst所指二叉排序树中，递归查找某关键字等于key的元素，若查找成功，返回指向该元素结点指针，否则返回空指针* /
{ 
    if (!bst) 
        return NULL;
    else 
        if (bst->key == key)
            return bst;/ *查找成功* /
        else
            if (bst->key > key)
                return SearchBST(bst->lchild, key);/ *在左子树继续查找* /
            else 
                return SearchBST(bst->rchild, key);/ *在右子树继续查找* /
}*/


BSTree  SearchBST(BSTree bst, KeyType key)
/*在根指针bst所指二叉排序树bst上，查找关键字等于key的结点，若查找成功，返回指向该元素结点指针，否则返回空指针*/
{ 
    BSTree q;
    q=bst;
    while(q)
    {
        if (q->key == key) 
            return q;  /*查找成功*/
        if (q->key > key)  
            q=q->lchild;  /*在左子树中查找*/
        else  
            q=q->rchild;  /*在右子树中查找*/
    }
    return NULL; /*查找失败*/
}/*SearchBST*/

BSTNode  * DelBST(BSTree t, KeyType  k) /*在二叉排序树t中删去关键字为k的结点*/
{
    BSTNode  *p, *f,*s ,*q;
    p=t; 
    f=NULL;
    while(p)  /*查找关键字为k的待删结点p*/
    { 
        if(p->key==k )  break;  /*找到则跳出循环*/
        f=p;   /*f指向p结点的双亲结点*/
        if(p->key>k)  
            p=p->lchild;
        else 
            p=p->rchild;
    } 
    if(p==NULL)  return t;  /*若找不到，返回原来的二叉排序树*/
    if(p->lchild==NULL)  /*p无左子树*/
    { 
        if(f==NULL) 
            t=p->rchild;  /*p是原二叉排序树的根*/
        else 
            if(f->lchild==p)  /*p是f的左孩子*/
                f->lchild=p->rchild ;  /*将p的右子树链到f的左链上*/
            else  /*p是f的右孩子*/
                f->rchild=p->rchild ;  /*将p的右子树链到f的右链上*/
            free(p);  /*释放被删除的结点p*/
    }
    else  /*p有左子树*/
    { 
        q=p; 
        s=p->lchild;
        while(s->rchild)  /*在p的左子树中查找最右下结点*/
        {
            q=s; 
            s=s->rchild;
        }
        if(q==p) 
            q->lchild=s->lchild ;  /*将s的左子树链到q上*/
        else 
            q->rchild=s->lchild;
        p->key=s->key;  /*将s的值赋给p*/
        free(s);
    }
    return t;
}  /*DelBST*/


void main()
{
    BSTree T;
    int k;
    BSTree result;
    printf("建立二叉排序树，请输入序列:\n");
    CreateBST(&T);
    printf("先序遍历输出序列为:");
    PreOrder(T);
    printf("\n请输入要查找的元素:");
    fflush(stdin);
    scanf("%d",&k);
    result = SearchBST(T,k);
    if (result != NULL)
        printf("要查找的元素为%d\n",result->key);
    else
        printf("未找到!\n");
    result = DelBST(T,k);
    PreOrder(result);
}

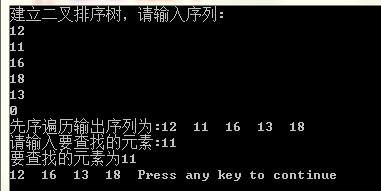
运行结果图：