高德地图是直线距离吗
This simple question “is a straight line linear?” came to my mind and couldn’t get out of it. It seems to be obvious, so it should have an obvious answer. However, when I dig into the research and try to find proof for this simple answer, I realized it’s more complex than I thought and more interesting!
这个简单的问题“直线是线性的吗?” 浮现在我的脑海,无法摆脱。 它似乎很明显,因此应该有一个明显的答案。 但是,当我深入研究并尝试找到这个简单答案的证据时,我意识到它比我想的还要复杂,也更有趣!
Linearity and non-linearity are terms commonly used in Data Science and Math. We try to figure out if a problem can be solved using linear or non-linear models, or if our data is linearly separable. If we widely use these terms, it’s important to understand them well, isn’t it? So what does it mean that something is linear by the book?
线性和非线性是数据科学和数学中常用的术语。 我们尝试找出是否可以使用线性或非线性模型解决问题,或者我们的数据是线性可分离的 。 如果我们广泛使用这些术语,那么一定要很好地理解它们,不是吗? 那么这本书意味着什么是线性的呢?
很简单……画出来! (It’s simple… draw it!)
Let’s think and try to visualize linearity. What comes to your mind? For me, it’s a simple straight line. Such a line is described by the following formula:
让我们思考并尝试可视化线性度 。 您想到什么? 对我来说,这是一条简单的直线。 此行由以下公式描述:
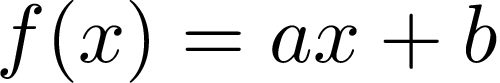
And indeed it is called a linear function [1]. In this formula, we have a variable x, and two parameters a and b. Let’s assume that a = 1, b = -2, and plot it:
实际上,它被称为线性函数 [1]。 在这个公式中,我们有一个变量x ,以及两个参数a和b 。 假设a = 1 , b = -2 ,并绘制它:
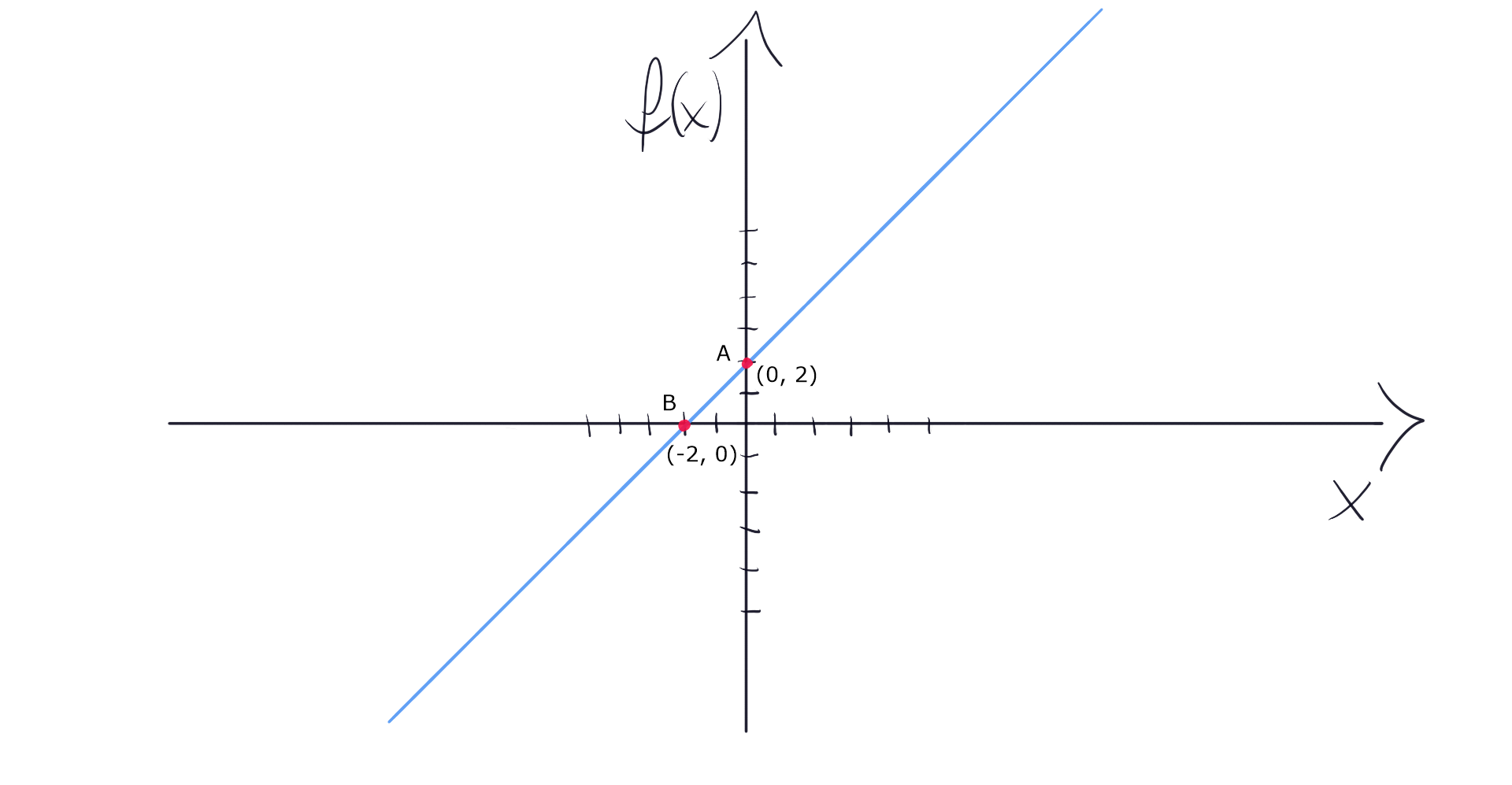
In the picture we can see that line goes through point A (0, 2) as f(0) = 2 and point B (-2, 0), because f(-2) = 0. That’s how we usually imagine linearity.
在图片中可以看出,线经过点A(0,2)为f(0)= 2和点B(-2,0),因为F(-2)= 0。 那就是我们通常想象线性的方式。
We also tend to think about linearity in terms of proportionality [2]. It means that the input is proportional to the output. Such intuitive thinking is natural for us, however, we need to remember that formally proportionality is a separate, wider term.
我们也倾向于根据比例来考虑线性[2]。 这意味着输入与输出成比例。 这种直觉的思维对我们来说很自然,但是,我们需要记住,正式的比例性是一个单独的,更广泛的术语。
By definition proportionality of two variables or quantities is a relation that occurs when ratio or product of these quantities is a constant. Having variables x and y, they are proportional if:
根据定义,两个变量或数量的比例关系是当这两个数量的比例或乘积为常数时发生的关系。 具有变量x和y ,它们在以下情况下成比例 :
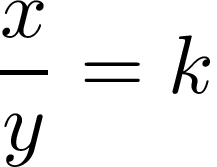
Where k is a constant. In this situation, if x is increasing, y also is increasing. The same applies when we decrease our variables, it’s proportional.
其中k是一个常数。 在这种情况下,如果x增加, y也增加。 当我们减少变量时也是如此,它是成比例的。
Variables are inversely proportional if their product is a constant:
如果变量的乘积为常数,则它们成反比 :
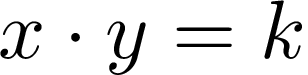
To check if it fits our intuition, we can transform this formula like this:
要检查它是否符合我们的直觉,我们可以像下面这样转换此公式:
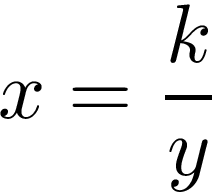
Assuming that k is greater than 0, and y is not equal to 0, while increasing y, x is decreasing. So everything is ok, it’s inversely proportional.
假设k大于0 ,并且y不等于0 ,而增加y ,则x减小。 因此,一切正常,它成反比。
书中的线性 (Linearity by the book)
Having in mind our intuitive thoughts on linearity, let’s confront it with the formal definition.
牢记我们对线性的直觉想法,让我们以正式定义面对它。
To call given relation, or a function, linear it should satisfy two properties (also known as superposition) [3]:
要调用给定的关系或函数,线性的应满足两个属性(也称为叠加 )[3]:
- Additivity 可加性
- Homogeneity 同质性
Additivity is described by the following formula:
通过以下公式描述可加性 :
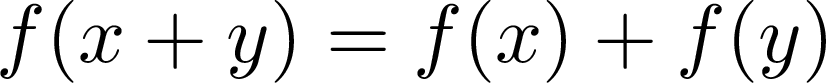
It means that the result of a function for the sum of inputs should be equal to the sum of the function’s results for each input separately.
这意味着输入总和的函数结果应分别等于每个输入的函数结果之和。
So let’s check if the function we drew before satisfies additivity. Just to quickly remind you, our function has parameters a = 1, b = -2, and its formula looks like this:
因此,让我们检查一下在满足可加性之前绘制的函数。 为了快速提醒您,我们的函数具有参数a = 1 , b = -2,其公式如下所示:
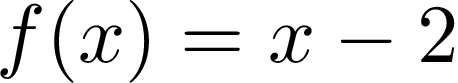
To check additivity we’ll assume that x = 2, y = 3. Now we need to calculate values of the function for the left and right side of additivity formula and check if they are equal. Let’s start with the left side:
为了检查可加性,我们假设x = 2 , y = 3 。 现在我们需要为可加性公式的左侧和右侧计算函数的值,并检查它们是否相等。 让我们从左侧开始:

Now let’s calculate the right side of the formula:
现在让我们计算公式的右边:
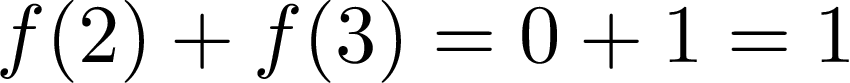
Oops, 3 is not equal 1, it means that our linear function does not satisfy additivity, which is a required property of linearity. So it’s not really linear…
糟糕,3不等于1,这表示我们的线性函数不满足可加性 ,这是线性的必需属性。 所以它不是线性的...
Maybe at least it’s homogeneous [3]? But first, what does it mean that function is homogeneous? Let’s say we multiply input x by a factor d and calculate the output of the function f(dx). Then let’s calculate the value of such expression df(x). According to homogeneity property, both results should be equal. It’s elegantly expressed by the simple formula:
也许至少是同质的 [3]? 但是首先,功能是同质的意味着什么? 假设我们将输入x乘以因子d,然后计算函数f(dx)的输出。 然后让我们计算这样的表达式df(x)的值 。 根据同质性,两个结果应相等。 简单的公式优雅地表达了这一点:
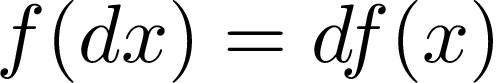
Now, we’ll do the same experiment as for additivity and check if our sample function satisfies homogeneity property. Let’s assume that d = 4, x = 2 and calculate the left side of the formula:
现在,我们将进行与可加性相同的实验,并检查我们的样本函数是否满足均一性。 假设d = 4 , x = 2并计算公式的左侧:
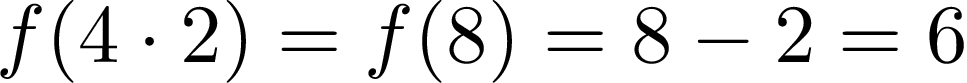
And then let’s calculate the right side:
然后让我们计算右边:
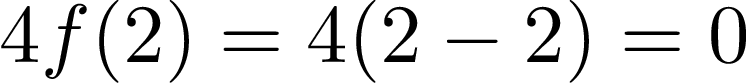
Hmm, 6 is definitely not equal 0, again our function doesn’t meet linearity requirements, this time in terms of homogeneity.
嗯,6绝对不等于0,这一次我们的函数不符合线性要求,这次是同质性。
哪个线性函数满足叠加要求? (Which linear function satisfies superposition?)
If our simple linear function doesn’t meet either of linearity requirements, which function does? Actually, it’s even simpler linear function with parameter b = 0:
如果我们的简单线性函数不满足任何一个线性要求,那么哪个函数呢? 实际上,它甚至是参数b = 0的更简单的线性函数:
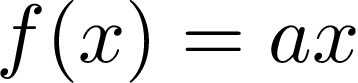
What is characteristic, functions described with such formulas go through the origin of the coordinates system (in the 2D system it’s (0,0)) [4].
用这种公式描述的函数的特征是经过坐标系的原点(在2D系统中为(0,0) )[4]。
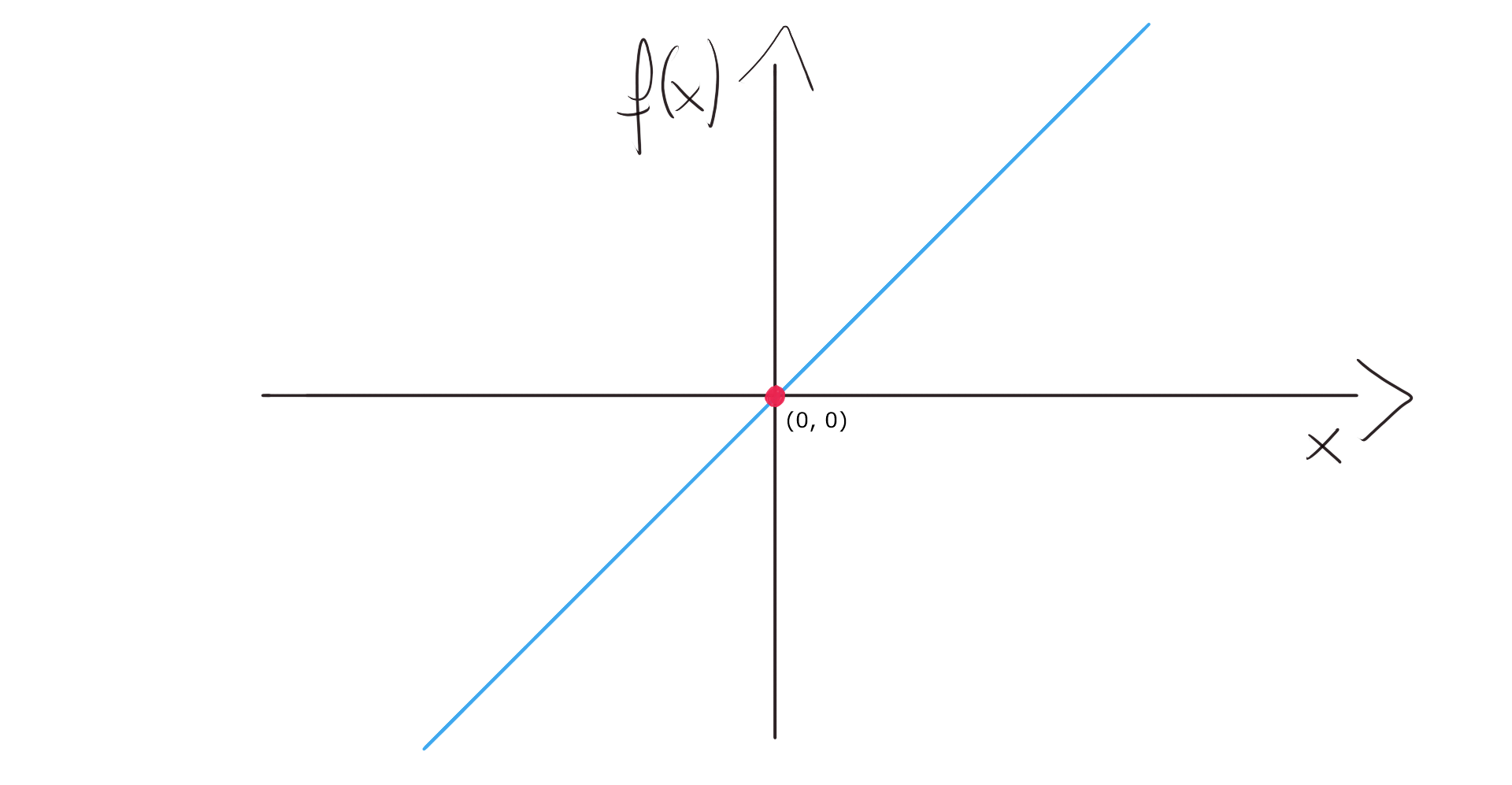
Let’s check if it really satisfies the requirements of linearity. We’ll assume that a=2, so our function is described by f(x) = 2x.
让我们检查一下它是否真的满足线性要求。 我们假设a = 2 ,因此我们的函数由f(x)= 2x来描述。
We go for additivity first. Calculating the left side of additivity formula for x = 2, y = 3, we get:
我们首先寻求可加性。 计算x = 2,y = 3的可加性公式的左侧,我们得到:

And for the right side of the formula we have:
对于公式的右侧,我们有:
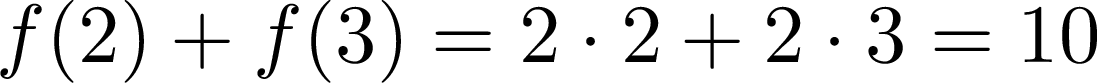
So far so good! 10 is equal to 10, so our function is additive, great. Let’s check homogeneity then.
到目前为止,一切都很好! 10等于10,所以我们的功能是可加的,很棒。 然后让我们检查同质性。
Assuming that d = 2, x = 4, we can calculate the left side of the homogeneity formula:
假设d = 2 , x = 4 ,我们可以计算出均匀性公式的左侧:
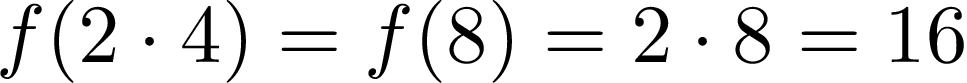
Ok, it’s 16, let’s check the right side of the formula:
好的,现在是16,让我们检查一下公式的右侧:
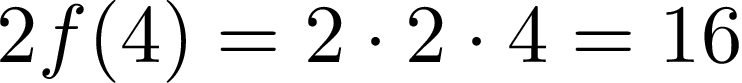
Yes! Our function is homogeneous. It satisfies both requirements of linearity, so we can tell it’s “truly” linear.
是! 我们的功能是同质的。 它满足线性的两个要求,因此我们可以说它是“真正的”线性。
那么这条直线是线性的吗? (So is this straight line linear, or not?)
The answer is: it depends. As you can see not all of the linear functions comply with strict requirements of linearity. Of course, it doesn’t mean that all of us make a huge mistake by using the term linear function. We just need to be careful in which context we use it.
答案是:这取决于。 如您所见,并不是所有的线性函数都符合严格的线性要求。 当然,这并不意味着我们所有人都通过使用线性函数一词犯了巨大的错误。 我们只需要谨慎使用我们的上下文即可。
Math is a really complex domain, containing a lot of different branches. The term linear function we use on a daily basis is perfectly correct in terms of calculus. In this context, every straight line is a linear function.
数学是一个非常复杂的领域,包含许多不同的分支。 就微积分而言,我们每天使用的线性函数一词是完全正确的。 在这种情况下,每条直线都是线性函数。
However, in terms of linear algebra only a subset of linear functions is truly linear (these with b = 0). It’s a wider context where we think in terms of linear mappings and linear systems (models that use linear operators). In this context, with strict requirements, a straight line may not be linear.
但是,就线性代数而言,只有线性函数的一个子集才是真正的线性(这些b = 0 )。 在更广泛的上下文中,我们根据线性映射和线性系统(使用线性算子的模型)进行思考。 在这种情况下,在严格的要求下,直线可能不是线性的。
Answering the original question we learned not only about linearity but also about the value of asking really obvious questions. They help us to obtain clarity and understanding of concepts we think we fully understand.
回答最初的问题,我们不仅学到了线性问题,而且学到了提出真正显而易见的问题的价值。 它们帮助我们获得对我们认为完全理解的概念的清晰度和理解。
参考书目: (Bibliography:)
翻译自: https://towardsdatascience.com/is-a-straight-line-linear-f9f491514e97
高德地图是直线距离吗
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








