ab 模拟_Ab测试第二部分的直观模拟

ab 模拟

In this post, I would like to invite you to continue our intuitive exploration of A/B testing, as seen in the previous post:

在本文中，我想邀请您继续我们对A / B测试的直观探索，如前一篇文章所示：

Resuming what we saw, we were able to prove through simulations and intuition that there was a relationship between Website Version and Signup since we were able to elaborate a test with a Statistical Power of 79% that allowed us to reject the hypothesis that states otherwise with 95% confidence. In other words, we proved that behavior as bias as ours was found randomly, only 1.6% of the time.

继续观察，我们可以通过模拟和直觉来证明网站版本和注册之间存在关系，因为我们能够以79％的统计功效精心制作一个测试，从而可以拒绝采用以下方法得出的假设： 95％的信心。 换句话说，我们证明了像我们这样的偏见行为是随机发现的，只有1.6％的时间。

Even though we were satisfied with the results, we still need to prove with a defined statistical confidence level that there was a higher-performing version. In practice, we need to prove our hypothesis that, on average, we should expect version F would win over any other version.

即使我们对结果感到满意，我们仍然需要以定义的统计置信度证明存在更高性能的版本。 在实践中，我们需要证明我们的假设，即平均而言，我们应该期望版本F会胜过任何其他版本。

开始之前 (Before we start)

Let us remember and explore our working data from our prior post, where we ended up having 8017 Dices thrown as defined by our Statistical Power target of 80%.

让我们记住并探索我们先前职位的工作数据，最终我们抛出了8017个骰子，这是我们80％的统计功效目标所定义的。

# Biased Dice Rolling FunctionDiceRolling <- function(N) {
    Dices <- data.frame()
    for (i in 1:6) {
      if(i==6) {
        Observed <- data.frame(Version=as.character(LETTERS[i]),Signup=rbinom(N/6,1,0.2))
      } else {
        Observed <- data.frame(Version=as.character(LETTERS[i]),Signup=rbinom(N/6,1,0.16))
      }
      Dices <- rbind(Dices,Observed)
    }
    return(Dices)
}# In order to replicateset.seed(11)
Dices <- DiceRolling(8017) # We expect 80% Power
t(table(Dices))

As a reminder, we designed an R function that simulates a biased dice in which we have a 20% probability of lading in 6 while a 16% chance of landing in any other number.

提醒一下，我们设计了一个R函数，该函数可以模拟有偏见的骰子，在该骰子中，我们有20％的概率在6中提货，而在其他数字中有16％的机会着陆。

Additionally, we ended up generating a dummy dataset of 8.017 samples, as calculated for 80% Power, that represented six different versions of a signup form and the number of leads we observed on each. For this dummy set to be random and have a winner version (F) that will serve us as ground truth, we generated this table by simulating some biased dice’s throws.

此外，我们最终生成了一个8017次幂计算的8.017个样本的虚拟数据集，该数据集表示六个不同版本的注册表单以及我们在每个表单上观察到的潜在客户数量。 为了使这个虚拟集是随机的，并且有一个获胜者版本(F)，它将用作我们的 基础事实，我们通过模拟一些有偏向的骰子投掷来生成此表。

The output:

输出：

higher frequency of observed F’s ( 更高频率的F ( 251) 251 )

Which should allow us to produce this report:

这应该使我们能够生成此报告：

Note the difference between our observed Signup Rate and the expected (designed) probabilities.

注意我们观察到的注册率和预期(设计)概率之间的差异。

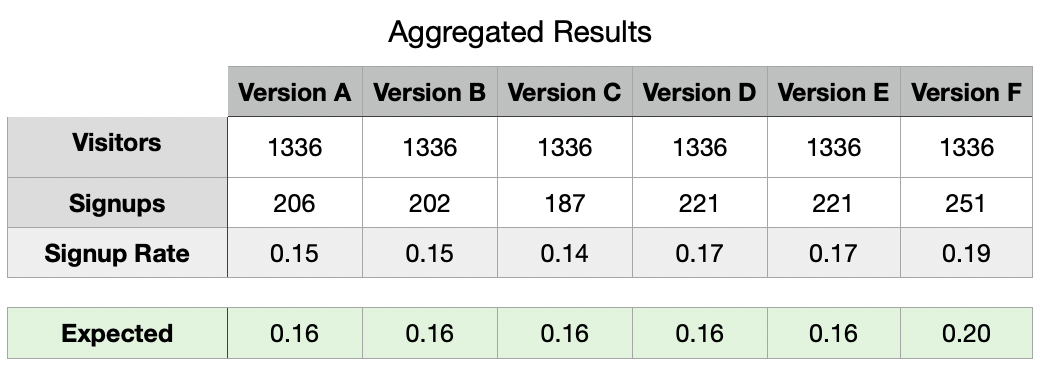
As seen above, we can observe different Signup Rates for our landing page versions. What is interesting about this is the fact that even though we planned a precise Signup Probability (Signup Rate), we got utterly different results between our observed and expected (planned) rates.

如上所述，对于目标网页版本，我们可以观察到不同的注册率。 有趣的是，即使我们计划了精确的注册概率(注册率)，我们在观察到的和预期的(计划的)利率之间却得到了截然不同的结果。

Let us take a pause and allow us to conduct a “sanity check” of say, Version C, which shows the highest difference between its Observed (0.14) and Expected (0.16) rates in order to check if there is something wrong with our data.

让我们暂停一下，让我们进行一次“健全性检查”，例如版本C，该版本显示其观测(0.14)和预期(0.16)速率之间的最大差异，以便检查我们的数据是否存在问题。

完整性检查 (Sanity Check)

Even though this step is not needed, it will serve us as a good starting point for building the intuition that will be useful for our primary goal.

即使不需要这一步骤，它也将为我们建立直觉提供一个很好的起点，这种直觉将对我们的主要目标有用。

As mentioned earlier, we want to prove that our results, even though initially different from what we expected, should not be far different from it since they vary based on the underlying probability distribution.

如前所述，我们想证明我们的结果，尽管最初与我们的预期有所不同，但应该与结果相差无几，因为它们基于潜在的概率分布而变化。

In other words, for the particular case of Version C, our hypothesis are as follows:

换句话说，对于版本C的特定情况，我们的假设如下：

我们为什么使用手段？ (Why did we use means?)

This particular case allows us to use both proportions or means since, as we designed our variables to be dichotomous with values 0 or 1, the mean calculation represents, in this case, the same value as our ratios or proportions.

这种特殊的情况下，允许我们使用这两个比例或办法，因为正如我们在设计变量是二分与值0或1，平均值计算表示，在这种情况下，相同的值作为我们的比率或比例。

# Results for Version C
VersionC <- Dices[which(Dices$Version==”C”),]# Mean calculation
mean(VersionC$Signup)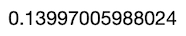

Version C Observed Mean

版本C观察到的平均值

p值 (p-Value)

We need to find our p-Value, which will allow us to accept or reject our hypothesis based on the probability of finding results “as extreme” as the one we got for Version C within the underlying probability distribution.

我们需要找到我们的p值，这将使我们能够基于在潜在概率分布内发现与版本C一样“极端”的结果的概率来接受或拒绝我们的假设。

This determination, meaning that our mean is significantly different from a true value (0.16), is usually addressed through a variation of the well-known Student Test called “One-Sample t-Test.” Note: since we are also using proportions, we could also be using a “Proportion Test”, though it is not the purpose of this post.

这种确定意味着我们的平均值与真实值(0.16)显着不同，通常通过一种著名的学生测验(称为“ 单样本t测验 ”)来解决。 注意：由于我们也使用比例，因此我们也可以使用“ 比例测试 ”，尽管这不是本文的目的。

To obtain the probability of finding results as extreme as ours, we would need to repeat our data collection process many times. Since this procedure is expensive and unrealistic, we will use a method similar to the resampling by permutation that we did in our last post called “Bootstrapping”.

为了获得发现与我们一样极端的结果的可能性，我们将需要重复多次数据收集过程。 由于此过程昂贵且不切实际，因此我们将使用类似于上一篇名为“ Bootstrapping”的文章中介绍的通过置换重采样的方法。

自举 (Bootstrapping)

Bootstrapping is done by reshuffling one of our columns, in this case Signups, while maintaining the other one fixed. What is different from the permutation resample we have done in the past is that we will allow replacement as shown below:

通过重新组合我们其中一列(在本例中为Signups)，同时保持另一列固定不变来进行引导。 与过去进行的排列重采样不同的是，我们将允许替换，如下所示：

Note that this time Signup data from our “Original Sample” is even repeated within our Replacements.

请注意，这次，我们的“替换品”中甚至重复了来自“原始样品”的注册数据。

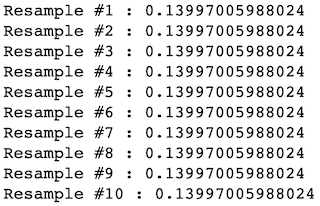
It is important to note that we need to allow replacement within this reshuffling process; otherwise, simple permutation will always result in the same mean as shown below.

重要的是要注意，我们需要允许在此改组过程中进行替换； 否则，简单的置换将始终产生如下所示的均值。

Let us generate 10 Resamples without replacement:

让我们生成10个重采样而不替换 ：

i = 0
for (i in 1:10) {
 Resample <- sample(VersionC$Signup,replace=FALSE);
 cat(paste("Resample #",i," : ",mean(Resample),"\n",sep=""));
 i = i+1;
}

Note that using permutation, they will always be the same.

请注意，使用置换，它们将始终相同。

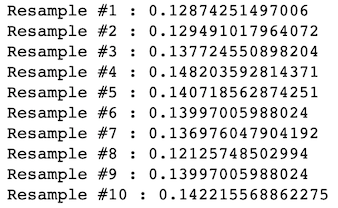
And 10 Resamples with replacement:

并替换 10个重采样：

i = 0
for (i in 1:10) {
 Resample <- sample(VersionC$Signup,replace=TRUE);
 cat(paste("Resample #",i," : ",mean(Resample),"\n",sep=""));
 i = i+1;
}

With a sample with replacement, they will vary according to a probability distribution.

对于替换样本，它们将根据概率分布而变化。

模拟 (Simulation)

Let us simulate 30k permutations of Version C with our data.

让我们用数据模拟版本C的30k排列。

# Let’s generate a Bootstrap and find our p-Value, Intervals and T-Scoresset.seed(1984)
Sample <- VersionC$Signup
score <- NULL
means <- NULL
for(i in 1:30000) {
 Bootstrap <- sample(Sample,replace = TRUE)
 means <- rbind(means,mean(Bootstrap))
 SimulationtTest <- tTest((Bootstrap-mean(Sample))/sd(Sample))
 tScores <- rbind(score,SimulationtTest)
}

As result, we got:

结果，我们得到：

mean equal to 0.14 均值等于0.14

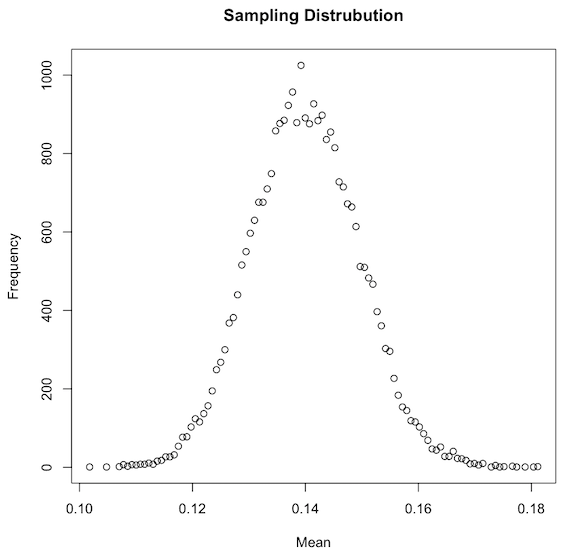
Initially, one might expect a distribution similar in shape, but centered around 0.16, therefore resembling the “true population mean” distribution. Even though we did not recreate the exact “ground truth distribution” (the one we designed), since it is now centered in the mean of our sample instead (0.14), we did recreate one that should have roughly the same shape and Standard Error, and that should contain within its range our true mean.

最初，人们可能会期望形状相似的分布，但以0.16为中心，因此类似于“ 真实总体均值 ”分布。 即使我们没有重新创建精确的“地面事实分布”(我们设计的)，因为它现在正以样本均值(0.14)为中心，所以我们确实重新创建了形状和标准误差大致相同的模型，并且应该在其真实范围内。

We can compare our “bootstrapped standard error” with the “true mean standard error” by using both Central Limit Theorem and the Standard Deviation formula for the Binomial Distribution.

通过使用中心极限定理和二项分布的标准偏差公式，我们可以将“ 自举标准误差 ”与“ 真实平均标准误差 ”进行比较。

Which allow us to obtain:

这使我们可以获得：

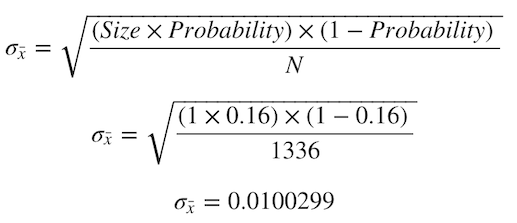
Which seems to be quite near to our bootstrapped Standard Error:

这似乎很接近我们自举的标准错误：

# Mean from sampling distributionround(sd(means),6)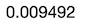

This data should be enough for us to approximate the original true mean distribution by simulating a Normal Distribution with a mean equal to 0.16 and a Standard Error of 0.01. We could find the percent of times a value as extreme as 0.14 is observed with this information.

通过模拟均值等于0.16且标准误差为0.01的正态分布，该数据应该足以使我们近似原始的真实均值分布。 通过此信息，我们可以找到一个值达到0.14的极高次数的百分比。

Estimated Sampling Distribution vs True Mean Distribution

估计抽样分布与真实均值分布

As seen above, both our True Mean Distribution (green) and our Bootstrapped Sample Distribution (blue) seems very similar, except the latter is centered around 0.14.

如上所示，我们的真实均值分布(绿色)和自举样本分布(蓝色)看起来非常相似，只是后者的中心在0.14左右。

At this point, we could solve our problem by either finding the percent of times a value as extreme as 0.14 is found within our true mean distribution (area colored in blue). Alternatively, we could find the percent of times a value as extreme as 0.16 is found within our bootstrapped sample distribution (area colored in green). We will proceed with the latter since this post is focused on simulations based solely on our sample data.

在这一点上，我们可以通过在真实的均值分布 (蓝色区域)中 找到等于0.14的极值的次数百分比来解决问题。 或者，我们可以 在自举样本分布 (绿色区域)中 找到一个值达到0.16的极限值的百分比 。 我们将继续进行后者，因为本文仅关注基于样本数据的模拟。

Resuming, we need to calculate how many times we observed values as extreme as 0.16 within our bootstrapped sample distribution. It is important to note that in this case, we had a sample mean (0.14) inferior to our expected mean of 0.16, but that is not always the case since, as we saw in our results, Version D got 0.17.

继续，我们需要计算在自举样本分布中观察到的值高达0.16的次数。 重要的是要注意，在这种情况下，我们的样本均值(0.14)低于我们的预期均值0.16，但并非总是如此，因为正如我们在结果中看到的，D版本的值为0.17。

In particular, we will perform a “two-tailed test”, which means finding the probability of obtaining values as extreme or as far from the mean as 0.16. Being our sample mean for Version C equal to 0.14, this is equivalent to say as low as 0.12 or as high as 0.16 since both values are equally extreme.

特别是，我们将执行“双尾检验”，这意味着找到获得的值作为极端 或 远离平均0.16的概率。 作为我们对于版本C的样本均值等于0.14，这等效于低至0.12或高至0.16，因为两个值都同样极端。

For this case, we found:

对于这种情况，我们发现：

# Expected Means, Upper and Lower interval (0.14 and 0.16)ExpectedMean <- 0.16
upper <- mean(means)+abs(mean(means)-ExpectedMean)
lower <- mean(means)-abs(mean(means)-ExpectedMean)
PValue <- mean(means <= lower | means >= upper)
Sum <- sum(means <= lower | means >= upper)
cat(paste(“We found values as extreme: “,PValue*100,”% (“,Sum,”/”,length(means),”) of the times”,sep=””))

This is our p-Value

这是我们的p值

Ok, we have found our p-Value, which is relatively low. Now we would like to find the 95% confidence interval of our mean, which would shed some light as of which values it might take considering a Type I Error (Alpha) of 5%.

好的，我们找到了相对较低的p值。 现在，我们想找到平均值的95％置信区间 ，这将为我们考虑5％的I型错误(Alpha)时取哪些值提供了一些启示 。

# Data aggregation
freq <- as.data.frame(table(means))
freq$means <- as.numeric(as.character(freq$means))# Sort Ascending for right-most proportion
freq <- freq[order(freq$means,decreasing = FALSE),]
freq$cumsumAsc <- cumsum(freq$Freq)/sum(freq$Freq)
UpperMean <- min(freq$means[which(freq$cumsumAsc >= 0.975)])# Sort Descending for left-most proportion
freq <- freq[order(freq$means,decreasing = TRUE),]
freq$cumsumDesc <- cumsum(freq$Freq)/sum(freq$Freq)
LowerMean <- max(freq$means[which(freq$cumsumDesc >= 0.975)])# Print Results
cat(paste(“95 percent confidence interval:\n “,round(LowerMean,7),” “,round(UpperMean,7),sep=””))

Note that 0.16 is not contained within this 95% confidence interval. 请注意，在此95％置信区间内不包含0.16。

Let us calculate our Student’s T-score, which is calculated as follows:

让我们计算学生的T分数，其计算方法如下：

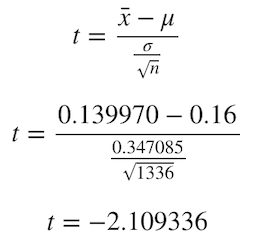
Since we already calculated this formula for every one of our 30k resamples, we can generate our critical t-Scores for 90%, 95%, and 99% confidence intervals.

由于我们已经为每30k次重采样计算了此公式，因此我们可以生成90％，95％和99％置信区间的临界t分数。

# Which are the T-Values expected for each Confidence level?
histogram <- data.frame(X=tScores)
library(dplyr)
histogram %>% 
 summarize(
 # Find the 0.9 quantile of diff_perm’s stat
 q.90 = quantile(X, p = 0.9),
 # … and the 0.95 quantile
 q.95 = quantile(X, p = 0.95),
 # … and the 0.99 quantile
 q.99 = quantile(X, p = 0.99)
 )

Simulated t-Values for 90%, 95% and 99%

90％，95％和99％的模拟t值

These values are very near the original Student’s Score Table for 1335 (N-1) degrees of freedom as seen here:

这些值非常接近原始学生的1335(N-1)自由度的成绩表，如下所示：

Students Score Table 学生成绩表

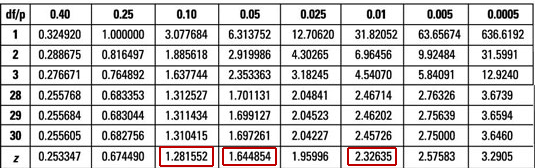
Resuming, we can observe that our calculated p-Value was around 3.69%, our 95% interval did not include 0.16, and our absolute t-Score of 2.1, as seen in our table, was just between the score of Alpha 0.05 and 0.01. All this seems to be coherent with the same outcome; we reject the null hypothesis with 95% confidence, meaning we cannot confirm that Version C’s true mean is equal to 0.16.

继续，我们可以观察到，我们计算出的p值约为3.69％，我们的95％区间不包括0.16，而我们的表中所见，我们的绝对t分数为2.1，正好在Alpha得分0.05和0.01之间。 所有这些似乎都与相同的结果相吻合。 我们以95％的置信度拒绝原假设 ，这意味着我们无法确认版本C的真实均值等于0.16。

We designed this test ourselves, and we know for sure our null hypothesis was correct. This concept of rejecting a true null hypothesis is called a False Positive or Type I Error, which can be avoided by increasing our current confidence Interval from 95% to maybe 99%.

我们自己设计了这个测试，并且我们肯定知道我们的零假设是正确的。 拒绝真实零假设的概念称为误报或I型错误，可以通过将当前的置信区间从95％增加到99％来避免。

So far, we have performed the equivalent of a “One-Sample t-Test” trough simulations, which implies we have determined whether the “sample mean” of 0.14 was statistically different from a known or hypothesized “population mean” of 0.16, which is our ground truth.

到目前为止，我们已经执行了与“ 单样本t检验 ”低谷模拟等效的操作，这意味着我们已确定0.14的“样本平均值”是否与已知或假设的0.16的“人口平均值”在统计上不同。是我们的基本真理。

For now, this will serve us as a building block for what is coming next since we will now proceed with a very similar approach to compare our Landing Versions between them to see if there is a winner.

目前，这将成为下一步工作的基础，因为我们现在将采用一种非常相似的方法来比较它们之间的着陆版本，以查看是否有赢家。

寻找我们的赢家版本 (Finding our winner version)

We have explored how to compare if a Sample Mean was statistically different from a known Population Mean; now, let us compare our Sample Mean with another Sample Mean.

我们已经探索了如何比较样本平均值是否与已知的总体平均值有统计学差异； 现在，让我们将样本均值与另一个样本均值进行比较。

For this particular example, let us compare Version F vs. Version A.

对于此特定示例，让我们比较版本F与版本A。

This procedure of comparing two independent samples is usually addressed with a test called “Unpaired Two sample t-Test”; it is unpaired since we will use different (independent) samples; we assume they behave randomly, with normal distribution and zero covariance, as we will later observe.

比较两个独立样本的过程通常通过称为“未配对的两个样本t检验”的测试解决 。 它是不成对的，因为我们将使用不同的(独立的)样本； 我们假设它们的行为随机，正态分布且协方差为零，我们将在后面观察到。

If we were to use the same sample, say at different moments in time, we would use a “Paired Two Sample t-Test” which, in contrast, compares two dependent samples, and it assumes a non-zero covariance which would be reflected in the formula.

如果我们使用相同的样本，例如在不同的时刻，我们将使用“ 成对的两个样本t检验 ”，相比之下，它比较两个相关样本 ，并且假设将反映出一个非零协方差在公式。

In simple words, we want to know how often we observe a positive difference in means, which is equivalent to say that Version F has a higher mean than Version A, thus, better performance. We know our current difference in means is as follows:

用简单的话说，我们想知道我们观察到均值出现正差的频率，这相当于说版本F的均值比版本A的均值高，因此性能更好。 我们知道我们目前的均值差异如下：

There’s a 3.37% positive difference between Sample F and Sample A

样品F和样品A之间存在3.37％的正差异

Since we know our Sample Means are just a single measurement of the real Population Mean for both Version F and Version A and not the true sample mean for neither one, we need to compute the estimated sample distribution for both versions like we did earlier. Unlike before, we will also calculate the difference in means for each resample to observe how it is distributed.

由于我们知道样本均值仅是对版本F和版本A的真实总体均值的单次测量，而不是对两个版本均不是真实的样本均值 ，因此我们需要像之前所做的那样计算两个版本的估计样本分布。 与以前不同，我们还将计算每次重采样的均值差，以观察其分布情况。

Let us simulate 40k samples with a replacement for Version F and Version A and calculate the difference in means:

让我们模拟40k样本，用版本F和版本A替代，并计算均值之差：

# Let’s select data from Version F and Version AVersionF <- Dices[which(Dices$Version==”F”),]
VersionA <- Dices[which(Dices$Version==”A”),]# We simulate 40kDiff <- NULL
meansA <- NULL
meansF <- NULL
for(i in 1:40000) {
 BootstrapA <- sample(VersionA$Signup,replace = TRUE)
 BootstrapF <- sample(VersionF$Signup,replace = TRUE)
 MeanDiff <- mean(BootstrapF)-mean(BootstrapA)
 Diff <- rbind(Diff,MeanDiff)
}# We plot the result
totals <- as.data.frame(table(Diff))
totals$Diff <- as.numeric(as.character(totals$Diff))
plot( totals$Freq ~ totals$Diff , ylab="Frequency", xlab="Difference",main="Sampling Difference Distrubution")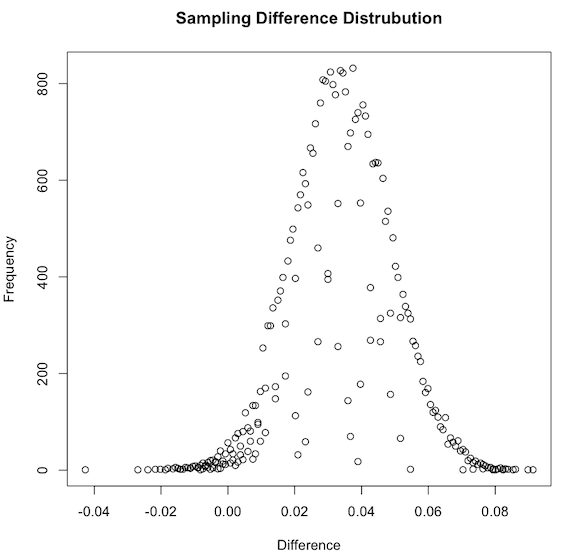

Sampling distribution of the difference between means

均值之间的抽样分布差异

As we might expect from what we learned earlier, we got a normally distributed shape centered in our previously calculated sample difference of 0.337. Like before, we also know the difference between the true population means for Versions A and F should be within the range of this distribution.

正如我们可能从我们先前所学到的那样，可以得到一个正态分布的形状，其中心位于我们先前计算的样本差异0.337中。 和以前一样，我们也知道版本A和版本F 的真实总体均值之差应在此分布范围内 。

Additionally, our bootstrap should have provided us a good approximation of the Standard Error of the difference between the true means. We can compare our “bootstrapped standard error” with the “true mean difference standard error” with both Central Limit Theorem and the Binomial Distribution.

此外，我们的自举程序应该为我们提供了真实均值之差的标准误差的良好近似值。 我们可以通过中心极限定理和二项分布来比较“ 自举标准误差 ”和“ 真实平均差标准误差 ” 。

Which allow us to obtain:

这使我们可以获得：

Expected Stander Error of the differences is 0.0148 with zero-covariance 差异的预期标准误差为0.0148，协方差为零

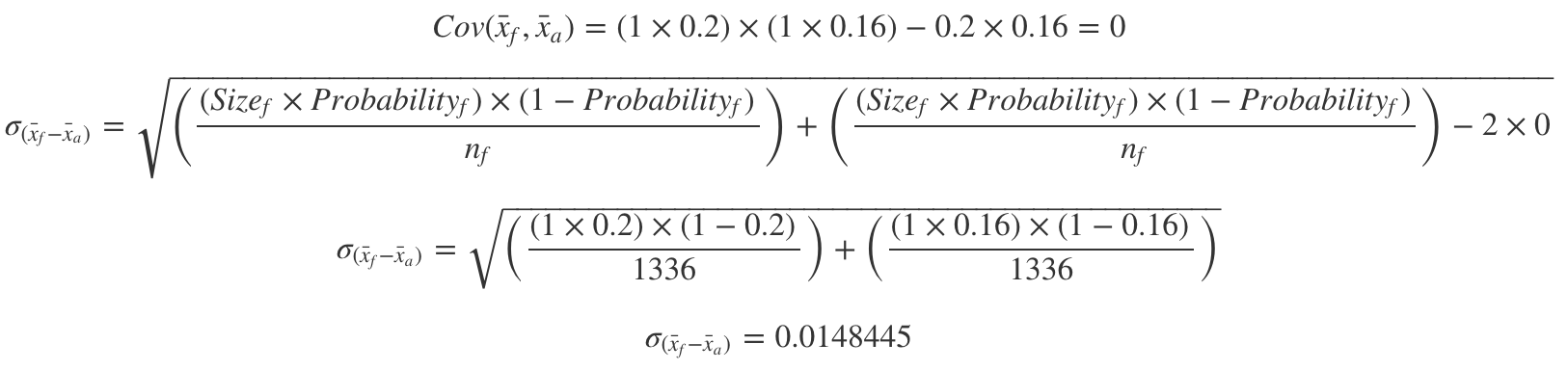
Just like before, it seems to be quite near our bootstrapped Standard Error for the difference of the means:

和以前一样，由于方式的不同，这似乎已经很接近我们的标准错误了：

# Simulated Standard Error of the differencesround(sd(Diff),6)

(very near our 0.0148 target)

(非常接近我们的0.0148目标)

As designed, we know the true expected difference of means is 0.04. We should have enough data to approximate a Normal Distribution with a mean equal to 0.04 and Standard Error of 0.0148, in which case we could find the percent of times a value as extreme as 0 is being found.

按照设计，我们知道均值的真实期望差是0.04。 我们应该有足够的数据， 平均等于 正态分布逼近到 0.0148 0.04和标准错误，在这种情况下，我们能找到的时间百分比值极端的被发现0。

This scenario is unrealistic, though, since we would not usually have population means, which is the whole purpose of estimating trough confidence intervals.

但是，这种情况是不现实的，因为我们通常不会拥有总体均值，这是估计谷底置信区间的全部目的。

Contrary to our previous case, in our first example, we compared our sample distribution of Version C to a hypothesized population mean of 0.16. However, in this case, we compare two individual samples with no further information as it would happen in a real A/B testing.

与我们先前的情况相反，在我们的第一个示例中，我们将版本C的样本分布与假设的总体平均值0.16进行了比较。 但是，在这种情况下，我们将比较两个单独的样本，而没有进一步的信息，因为这将在实际的A / B测试中发生。

In particular, we want to prove that Version F is superior to Version A, meaning that the difference between means is greater than zero. For this case, we need to perform a “One-Tailed” test answering the following question: which percent of the times did we observe a difference in means greater than zero?

特别是，我们要证明版本F优于版本A，这意味着均值之间的差大于零。 对于这种情况，我们需要执行“单尾”测试，回答以下问题： 在平均百分比中，观察到差异大于零的百分比是多少？

Our hypothesis is as follows:

我们的假设如下：

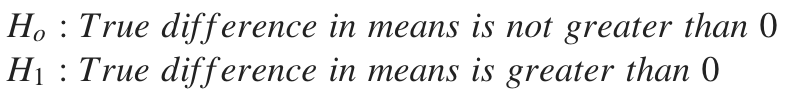
The answer:

答案：

# Percent of times greater than Zeromean(Diff > 0)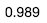

This means P-Value = 0.011

这意味着P值= 0.011

Since our p-Value represents the times we did not observe a difference in mean higher than Zero within our simulation, we can calculate it to be 0.011 (1–0.989). Additionally, being lower than 0.05 (Alpha), we can reject our null hypothesis; therefore, Version F had a higher performance than Version A.

由于我们的p值代表我们在仿真中未观察到均值大于零的差异的时间，因此我们可以将其计算为0.011(1-0.989)。 此外，如果低于0.05(Alpha)，我们可以拒绝原假设 ； 因此，F 版本比A版本具有更高的性能。

If we calculate both 95% confidence intervals and t-Scores for this particular test, we should obtain similar results:

如果我们为此特定测试计算95％的置信区间和t分数，则我们应获得类似的结果：

Confidence interval at 95%:

置信区间为95％：

# Data aggregation
freq <- as.data.frame(table(Diff))
freq$Diff <- as.numeric(as.character(freq$Diff))# Right-most proportion (Inf)UpperDiff <- Inf# Sort Descending for left-most proportion
freq <- freq[order(freq$Diff,decreasing = TRUE),]
freq$cumsumDesc <- cumsum(freq$Freq)/sum(freq$Freq)
LowerDiff <- max(freq$Diff[which(freq$cumsumDesc >= 0.95)])# Print Results
cat(paste(“95 percent confidence interval:\n “,round(LowerDiff,7),” “,round(UpperDiff,7),sep=””))

Note our right-most interval is Infinite, since we did a one tailed test.

注意我们最右边的间隔是无限，因为我们进行了一次尾巴测试。

As expected, our confidence interval tells us that with 95% confidence, we should expect a difference of at least 0.0097, which is above zero; therefore, it shows a better performance.

不出所料，我们的置信区间告诉我们，在95％的置信度下，我们应该期望至少有0.0097的差异，该差异大于零。 因此，它表现出更好的性能。

Unpaired Two-Sample t-Test score:

未配对的两次样本t检验得分：

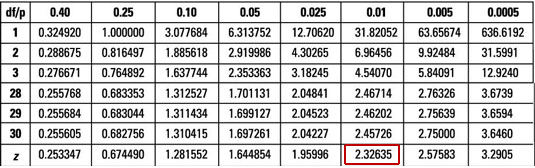
Similar to our previous values, checking our t-Table for T=2.31 and 2653 Degrees of Freedom we also found a p-Value of roughly 0.01

与我们之前的值类似，检查t表中的T = 2.31和2653自由度，我们还发现p值大约为0.01

Students Score Table 学生成绩表

成对比较 (Pairwise Comparison)

So far, we have compared our Landing Page Version C with a hypothesized mean of 0.16. We have also compared Version F with Version A and found which was the highest-performer.

到目前为止，我们已经将目标网页版本C与假设的平均值0.16进行了比较。 我们还将版本F和版本A进行了比较，发现性能最高。

Now we need to determine our absolute winner. We will do a Pairwise Comparison, meaning that we will test every page with each other until we determine our absolute winner if it exists.

现在我们需要确定我们的绝对赢家。 我们将进行成对比较，这意味着我们将相互测试每一页，直到我们确定绝对赢家(如果存在)。

Since we will make a One-Tailed test for each and we do not need to test a version with itself, we can reduce the total number of tests as calculated below.

由于我们将为每个测试进行一次测试，因此我们不需要自己测试版本，因此可以减少如下计算的测试总数。

# Total number of versionsVersionNumber <- 6# Number of versions comparedComparedNumber <- 2# Combinationsfactorial(VersionNumber)/(factorial(ComparedNumber)*factorial(VersionNumber-ComparedNumber))

As output we obtain: 15 pair of tests.

作为输出，我们获得： 15对测试。

Note, we need to find only values in green. Whites will be 1- Corresponding Pair (GreenValue)

注意，我们只需要找到绿色的值。 白人将是1-对应对(GreenValue)

We will skip the process of repeating this 15 times, and we will jump straight to the results, which are:

我们将跳过重复此过程15次的过程，然后直接跳转到以下结果：

In red we have marked whenever our p-Value < Alpha (0.05) which means Row Version was superior than Column Version.

用红色标记时，我们的p值<Alpha(0.05)表示行版本优于列版本。

As seen above, we have managed to find that Version F had better performance than both versions A, C, and was almost better performing than B, D, and E, which were close to our selected Alpha of 5%. In contrast, Version C seems to be an extraordinary case since, with both D and E, it seems to have a difference in means greater than zero, which we know is impossible since all three were designed with an equivalent probability of 0.16.

如上所示，我们设法发现版本F的性能优于版本A，C，并且几乎比版本B，D和E更好，后者接近我们选择的5％的Alpha。 相反，版本C似乎是一个特殊情况，因为对于D和E，它的均方差似乎都大于零，我们知道这是不可能的，因为所有这三个均以0.16的等效概率进行设计。

In other words, we have failed to reject our Null Hypothesis at a 95% confidence even though it is false for F vs. B, D, and C; this situation (Type II Error) could be solved by increasing our Statistical Power. In contrast, we rejected a true null hypothesis for D vs. C and E vs. C, which indicates we have incurred in a Type I Error, which could be solved by defining a lower Alpha or Higher Confidence level.

换句话说， 即使 F vs 是错误的 ，我们也无法以95％的置信度拒绝零假设 。 B， D和C; 这种情况(II型错误)可以通过提高统计功效来解决。 相反，我们拒绝了 D vs 的真实零假设 。 C和E 与 。 C，表示我们发生了I型错误 ，可以通过定义较低的Alpha或较高的置信度来解决。

We indeed designed our test to have an 80% statistical power. However, we designed it solely for testing differences between our total observed and expected frequencies and not for testing differences between individual means. In other words, we have switched from a “Chi-Squared Test” to an “Unpaired Two-Sample t-Test”.

实际上，我们将测试设计为具有80％的统计功效。 然而，我们设计它只是为了测试我们的 总 观察和期望频率 之间 ，而不是用于测试 个别 手段 之间的差异 的差异 。 换句话说，我们已经从“ 卡方检验”切换为““非配对两样本t检验””。

统计功效 (Statistical Power)

We have obtained our results. Even though we could use them as-is and select the ones with the highest overall differences, such as the ones with the lowest P-Values, we might want to re-test some of the variations in order to be entirely sure.

我们已经获得了结果。 即使我们可以按原样使用它们并选择总体差异最大的差异(例如P值最低的差异)，我们也可能要重新测试某些差异以完全确定。

As we saw in our last post, Power is calculated as follows:

正如我们在上一篇文章中所见，Power的计算如下：

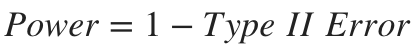
Similarly, Power is a function of:

同样，Power是以下功能之一：

• Our significance criterion is our Type I Error or Alpha, which we decided to be 5% (95% confidence).

  我们的显着性标准是I型错误或Alpha，我们决定为5％(置信度为95％)。

• Effect Magnitude or Size: This represents the difference between our observed and expected values regarding the standardized statistic of use. In this case, since we are using a Student’s Test Statistic, this effect (named d) is calculated as the “difference between means” divided by the “Pooled Standard Error”. It is usually categorized as Small (0.2), Medium (0.5), and Large (0.8).

  效果幅度或大小 ：这表示我们在有关标准化使用统计方面的观察值与期望值之间的差异。 在这种情况下，由于我们使用的是学生的测试统计量，因此将这种效应(称为d )计算为“ 均值之差”除以“ 合并标准误差” 。 通常分为小(0.2)，中(0.5)和大(0.8)。

• Sample size: This represents the total amount of samples (in our case, 8017).

  样本数量 ：代表样本总数(在我们的情况下为8017)。

效果幅度 (Effect Magnitude)

We designed an experiment with a relatively small effect magnitude since our Dice was only biased in one face (6) with only a slight additional chance of landing in its favor.

我们设计的实验的效果等级相对较小，因为我们的骰子仅偏向一张脸(6)，只有很少的其他机会落在其脸上。

In simple words, our effect magnitude (d) is calculated as follows:

简而言之，我们的影响幅度(d)计算如下：

(note the relationship with the t-Score formula we previously used)

(请注意与我们之前使用的t-Score公式的关系)

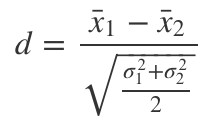
If we calculate this for the expected values of Version F vs. Version A, using the formulas we have learned so far, we obtain:

如果我们使用到目前为止所学的公式针对版本F与版本A的期望值进行计算，则可以获得：

Note that our calculated effect size is 50% of what’s usually considered a “small effect”

请注意，我们计算出的效果大小是通常认为是“小效果”的50％

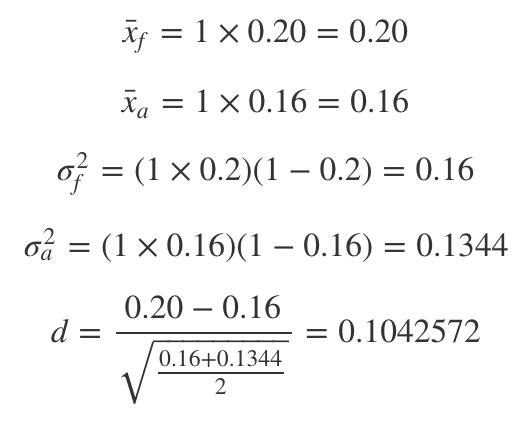
样本量 (Sample Size)

As we commented in our last post, we can expect an inverse relationship between sample sizes and effect magnitude. The more significant the effect, the lower the sample size needed to prove it at a given significance level.

正如我们在上一篇文章中评论的那样，我们可以预期样本量与效应量之间存在反比关系。 效果越显着，在给定的显着性水平下证明该结果所需的样本量越少。

Let us try to find the sample size needed in order to have a 90% Power. We can solve this by iterating different values of N until we minimize the difference between our Expected Power and the Observed Power.

让我们尝试找到拥有90％功效的所需样本量。 我们可以通过迭代N的不同值来解决此问题，直到我们将期望功率和观察功率之间的差异最小化为止。

# Basic example on how to obtain a given N based on a target Power.
# Playing with initialization variables might be needed for different scenarios.
set.seed(11)
CostFunction <- function(n,d,p) {
  df <- (n - 1) * 2
  tScore <- qt(0.05, df, lower = FALSE)
  value <- pt(tScore , df, ncp = sqrt(n/2) * d, lower = FALSE)
  Error <- (p-value)^2
  return(Error)
}
SampleSize <- function(d,n,p) {
  # Initialize variables
  N <- n
  i <- 0
  h <- 0.000000001
  LearningRate <- 3000000
  HardStop <- 20000
  power <- 0
  # Iteration loop
  for (i in 1:HardStop) {
    dNdError <- (CostFunction(N + h,d,p) - CostFunction(N,d,p)) / h
    N <- N - dNdError*LearningRate
    tLimit <- qt(0.05, (N - 1) * 2, lower = FALSE)
    new_power <- pt(tLimit , (N- 1) * 2, ncp = sqrt(N/2) * d, lower = FALSE)
    if(round(power,6) >= p) {
      cat(paste0("Found in ",i," Iterations\n"))
      cat(paste0("   Power: ",round(power,2),"\n"))
      cat(paste0("   N: ",round(N)))
      break();
    }
    power <- new_power
    i <- i +1
  }
}
set.seed(22)
SampleSize((0.2-0.16)/sqrt((0.16+0.1344)/2),1336,0.9)

As seen above, after different iterations of N, we obtained a recommended sample of 1576 per dice to have a 0.9 Power.

如上所示，在N的不同迭代之后，我们获得了每个骰子 1576的推荐样本，具有0.9的功效。

Let us repeat the experiment from scratch and see which results we get for these new sample size of 9456 (1575*6) as suggested by aiming a good Statistical Power of 0.9.

让我们从头开始重复实验，看看针对9456(1575 * 6)的这些新样本大小，我们通过将0.9的良好统计功效作为目标而获得了哪些结果。

# Repeat our experiment with sample size 9446set.seed(11)
Dices <- DiceRolling(9456) # We expect 90% Power
t(table(Dices))

Version F seems to be the winner again with 339 Signups

版本F似乎再次以339个注册获胜

Let us make a fast sanity check to see if our experiment now has a Statistical Power of 90% before we proceed; this can be answered by asking the following question:

让我们进行快速的理智检查，看看我们的实验在进行之前是否现在具有90％的统计功效； 可以通过提出以下问题来回答：

• If we were to repeat our experiment X amount of times and calculate our P-Value on each experiment, which percent of the times, we should expect a P-Value as extreme as 5%?
  如果我们要重复实验X次并在每个实验中计算出我们的P值(占百分比的百分比)，那么我们应该期望P值达到5％的极限吗？

Let us try answering this question for Version F vs. Version A:

让我们尝试回答版本F与版本A的问题：

# Proving by simulation
MultipleDiceRolling <- function(k,N) {
  pValues <- NULL
  for (i in 1:k) {
    Dices <- DiceRolling(N)    
    VersionF <- Dices[which(Dices$Version=="F"),]
    VersionA <- Dices[which(Dices$Version=="A"),]
    pValues <- cbind(pValues,t.test(VersionF$Signup,VersionA$Signup,alternative="greater")$p.value)
    i <- i +1
  }
  return(pValues)
}# Lets replicate our experiment (9456 throws of a biased dice) 10k times
start_time <- Sys.time()
Rolls <- MultipleDiceRolling(10000,9456)
end_time <- Sys.time()
end_time - start_time

How many times did we observe P-Values as extreme as 5%?

我们观察过多少次P值高达5％？

cat(paste(length(which(Rolls <= 0.05)),"Times"))

Which percent of the times did we observe this scenario?

我们观察到这种情况的百分比是多少？

Power <- length(which(Rolls <= 0.05))/length(Rolls)
cat(paste(round(Power*100,2),"% of the times (",length(which(Rolls <= 0.05)),"/",length(Rolls),")",sep=""))

As calculated above, we observe a Power equivalent to roughly 90% (0.896), which proves our new sample size works as planned. This implies we have a 10% (1 — Power) probability of making a Type II Error or, equivalently, a 10% chance of failing to reject our Null Hypothesis at a 95% confidence interval even though it is false, which is acceptable.

根据上面的计算，我们观察到的功效大约等于90％(0.896)，这证明了我们新的样本量能按计划进行。 这意味着我们有10％(1- Power)发生II型错误的概率，或者等效地， 即使它为假 ，也有10％的机会未能以95％的置信区间拒绝零假设 ，这是可以接受的。

绝对赢家 (Absolute winner)

Finally, let us proceed on finding our absolute winner by repeating our Pairwise Comparison with these new samples:

最后，让我们通过对这些新样本重复成对比较来找到我们的绝对赢家：

In red we have marked whenever our p-Value < Alpha (0.05) which means Row Version was superior than Column Version.

用红色标记时，我们的p值<Alpha(0.05)表示行版本优于列版本。

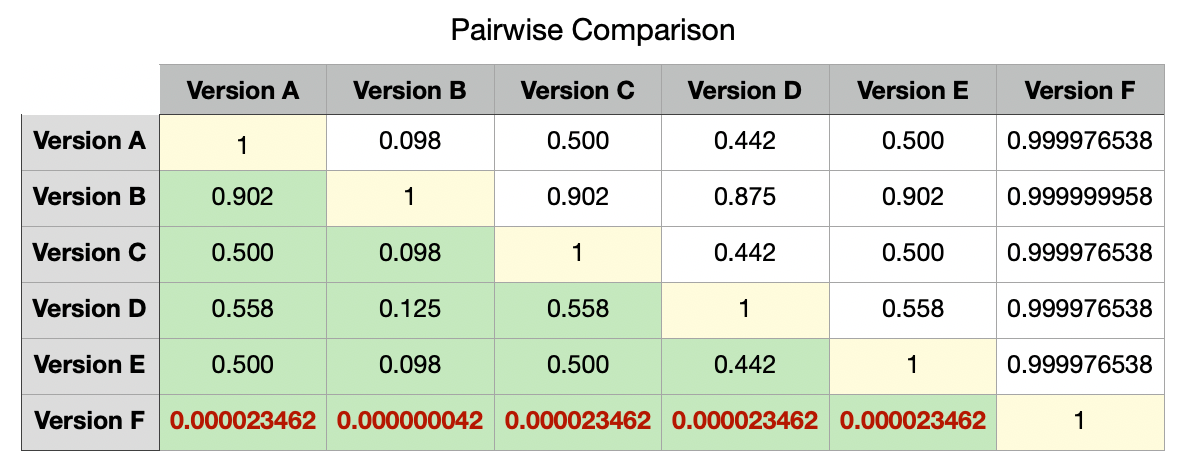
As expected, our absolute winner is Version F amongst all other versions. Additionally, it is also clear now that there is no significant difference between any other version’s true means.

不出所料，我们的绝对赢家是所有其他版本中的F版本。 此外，现在也很清楚，其他版本的真实含义之间没有显着差异。

最后的想法 (Final Thoughts)

We have explored how to perform simulations on two types of tests; Chi-Squared and Student’s Tests for One and Two Independent Samples. Additionally, we have examined some concepts such as Type I and Type II errors, Confidence Intervals, and the calculation and Interpretation of the Statistical Power for both scenarios.

我们探索了如何对两种类型的测试进行仿真。 一和两个独立样本的卡方检验和学生检验。 此外，我们还研究了一些概念，例如I型和II型错误，置信区间以及两种情况下的统计功效的计算和解释。

It is essential to know that we would save much time and even achieve more accurate results by performing such tests using specialized functions in traditional use-case scenarios, so it is not recommended to follow this simulation path. In contrast, this type of exercise offers value in helping us develop a more intuitive understanding, which I wanted to achieve.

必须知道，通过在传统用例场景中使用专门功能执行此类测试，我们将节省大量时间，甚至可以获得更准确的结果，因此不建议您遵循此仿真路径。 相比之下，这种锻炼方式可以帮助我们建立更直观的理解，这是我想要实现的。

If you have any questions or comments, do not hesitate to post them below.

如果您有任何问题或意见，请随时在下面发布。

翻译自: https://towardsdatascience.com/intuitive-simulation-of-a-b-testing-part-ii-8902c354947c

ab 模拟