数据算法结构哪部分最难_解决算法中最困难的部分

数据算法结构哪部分最难

If you have been solving algorithms questions for a while, you will notice specific patterns and topics are just more challenging than usual. Before we dive deeper into these topics, I understand everyone has their own most challenging algorithm topics out there. However, I am here stating my own opinion on what I have seen so far that I feel are the most challenging algorithms topics. I know I am not alone, and I believe my intuition aligns with many folks out there.

如果您已经解决算法问题已有一段时间了，您会发现特定的模式和主题比平时更具挑战性。 在我们深入探讨这些主题之前，我了解每个人都有他们自己最具挑战性的算法主题。 但是，我在这里对到目前为止所看到的内容发表自己的看法，我认为这是最具挑战性的算法主题。 我知道我并不孤单，而且我相信我的直觉与许多人保持一致。

动态编程 (Dynamic Programming)

Dynamic Programming (DP) is one of the most well-known topics that everyone struggles with. It feels like there is no shortcut way of making it simple. It requires a lot of practice and repetition of solving those types of questions to get good at it. Dynamic programming is a method for solving a complex problem by breaking it down into a collection of simpler subproblems, solving each subproblem just once, and storing their solutions. In other words, it is a way of approach and pattern solving problems, breaking it down into smaller pieces, and reducing duplication of those smaller pieces by storing them somehow. Dynamic Programming is a trendy challenging topic in leetcode, where everyone on the discussion page is talking about it.

动态编程(DP)是每个人都在努力解决的最著名的主题之一。 感觉没有简化它的捷径。 要熟练掌握它，需要进行大量练习和重复解决这些类型的问题。 动态编程是一种解决复杂问题的方法，可以将其分解为更简单的子问题的集合，每个子问题仅解决一次，然后存储其解决方案。 换句话说，这是一种解决问题和模式的方法，可以将问题分解为较小的部分，并通过某种方式存储它们来减少这些较小部分的重复。 动态编程是leetcode中一个新潮挑战性话题，讨论页面上的每个人都在谈论它。

最佳化 (Optimizing)

You will be surprised how hard it is to optimize the time and space complexity of your code. This topic is one of the most iconic topics among technical interviews. Sometimes getting the right answer is not hard, but making the code more efficient and abstract are two different stories. One example below, as you can see, the question is simple to answer if it is without the big-o notation constraint. Nevertheless, if it evolves big-o notation, which you need to optimize your code run time complexity, then it might pause you for a bit and think.

您将惊讶于优化代码的时间和空间复杂性有多么困难。 该主题是技术采访中最具标志性的主题之一。 有时候，获得正确答案并不难，但是使代码更高效和抽象则是两个不同的故事。 如您所见，下面的一个示例如果没有big-o符号约束，则很容易回答这个问题。 但是，如果它演变为大符号，则需要优化代码运行时的复杂度，那么它可能会使您停下来思考一下。

Asking the algorithm should run in O(n) complexity.

要求算法应以O(n)复杂度运行。

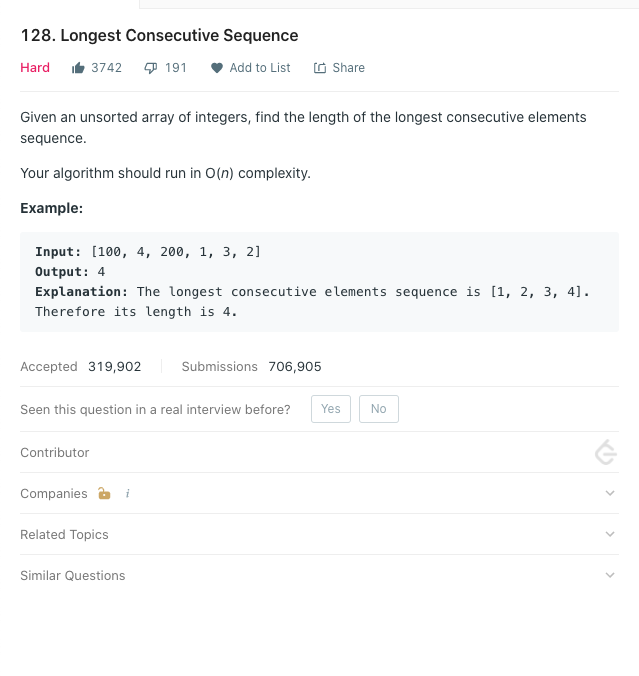
Getting the right answer with the Brute Force way for solving this problem is not hard at all, but with O(n) time complexity requires time and effort to solve. Here is another example.

用蛮力方法来解决这个问题并不难，但是使用O(n)时间复杂性需要时间和精力来解决。 这是另一个例子 。

实作 (Implementation)

There are two parts of problem-solving in algorithm questions. The first is coming up with the algorithm, and the second is implementing the algorithm. Coming up with algorithms could be easy sometimes. With the understanding of data structures, knowledge could support the approach of coming with algorithms for the problem. On the other hand, implementing the algorithm could be difficult. Many hard questions in leetcode give you hints on what kind of data structures/topics to solve the problem with, yet you are still struggling to solve them. Implementing hard algorithms problems is hard, even when you understand the question well and know what kind of data structure/topics to approach them. What’s even more challenging is algorithms questions that rely on massive implementation, such as questions you can easily find in competitive programming contests and high school/college programming contests. There is no doubt the difficulties of these problems are not a match.

算法问题有两部分解决问题。 第一个是提出算法，第二个是实现算法。 有时想出算法很容易。 通过对数据结构的理解，知识可以支持伴随问题算法的方法。 另一方面，实现该算法可能很困难。 leetcode中的许多难题向您提示了使用哪种数据结构/主题来解决问题，但您仍在努力解决这些问题。 即使您很好地理解了问题并知道采用哪种数据结构/主题来解决问题，也很难实现算法难题。 更具挑战性的是依赖大规模实现的算法问题，例如您可以在竞争性编程竞赛和高中 / 大学编程竞赛中轻松找到的问题。 毫无疑问，这些问题的难处是无法比拟的。

The International Collegiate Programming Contest, known as the ICPC, is an annual multi-tiered competitive programming competition among the world's universities.

国际大学编程竞赛称为ICPC，是世界大学之间的年度多层次竞争性编程竞赛。

数学技巧 (Math Tricks)

Have you heard many folks say that you need to know some math to understand how to program? Well, some specific algorithms questions require you to understand some math theory to solve them, but in terms of programming, there are two completely different stories. Nowadays, there is Google, where you can search for beautiful theories and study from them. However, specific math theories are hard and tedious, not as simple as everyone learns in high school Pythagoras’ Theorem.

您是否听说过很多人说您需要了解一些数学才能理解如何编程？ 好吧，一些特定的算法问题需要您了解一些数学理论来解决它们，但是就编程而言，有两个完全不同的故事。 如今，有了Google，您可以在其中搜索美丽的理论并从中学习。 但是，特定的数学理论既困难又乏味，并不像每个人在中学毕达哥拉斯定理中所学的那样简单。

To name a few, number theory, modular arithmetic, game theory, probability theory, graph theory, computational geometry, permutations, combinations, etc. There are particular algorithm problems straight up asking math topics; all you need to do is a study and implement them with the theoretical knowledge approach.

仅举几例，数论，模算术，博弈论，概率论，图论，计算几何，置换，组合等 。 有一些特殊的算法问题直接询问数学主题。 您需要做的只是研究并以理论知识的方法实施它们。

You can find these types of questions a lot among competitive programming contests, Olympiad among high schools (IOI), and college programming contests (ICPC). Although there are also challenging problems in leetcode that evolve with math topics, however, the one that is on coding competition is not comparable. Check out here and here for some examples that require understanding some mathematical concepts to solve the problem.

在竞争性编程竞赛，高中奥林匹克竞赛( IOI )和大学编程竞赛( ICPC )中，您会发现很多这类问题。 尽管leetcode中也存在一些挑战性的问题，这些问题随着数学主题的发展而发展，但是在编码竞赛中却是不可比拟的。 在此处和此处查看一些示例，这些示例需要了解一些数学概念来解决问题。

结论 (Conclusion)

So there you go! These are the topics and patterns that I found that are difficult in solving algorithm questions. Of course, I believe everyone has a unique experience of having different categories of the hardest things to solve in algorithms. If you find something challenging topics or patterns in solving algorithms that are not listed here, please let me know. As always, I hope you enjoy my article and thanks for taking the time to read.

所以你去了！ 这些是我发现很难解决算法问题的主题和模式。 当然，我相信每个人都有独特的经验，需要在算法中解决最困难的问题的不同类别。 如果您在解决此处未列出的算法时发现一些具有挑战性的主题或模式，请告诉我。 与往常一样，希望您喜欢我的文章，并感谢您抽出宝贵的时间阅读。

翻译自: https://medium.com/the-innovation/the-hardest-part-of-solving-algorithms-a150ae2c99d7

数据算法结构哪部分最难