梯度下降法 梯度上升法
深层加固学习介绍— 19 (DEEP REINFORCEMENT LEARNING EXPLAINED — 19)
This is a new post devoted to Policy-Gradient Methods, in the “Deep Reinforcement Learning Explained” series. Policy-Gradient methods are a subclass of Policy-Based methods that estimate an optimal policy’s weights through gradient ascent.
这是“ 深度强化学习解释 ”系列中专门讨论策略梯度方法的新文章。 策略梯度方法是基于策略的方法的子类,该方法通过梯度上升来估计最佳策略的权重。

Intuitively, gradient ascent begins with an initial guess for the value of policy’s weights that maximizes the expected return, then, the algorithm evaluates the gradient at that point that indicates the direction of the steepest increase of the function of expected return, and so we can make a small step in that direction. We hope that we end up at a new value of policy’s weights for which the value of the expected return function is a little bit larger. The algorithm then repeats this process of evaluating the gradient and taking steps until it considers that it is eventually reached the maximum expected return.
直观地讲,梯度上升首先是对使期望收益最大化的保单权重值的初始猜测,然后,算法在该点处评估梯度,该梯度指示期望收益函数的最大增加方向,因此我们可以朝这个方向迈出一小步。 我们希望最终得到一个新的政策权重值,期望收益函数的值会更大。 然后,该算法重复此评估梯度并采取步骤的过程,直到它认为最终达到最大预期收益为止。
Although we have coded a deterministic policy in the previous post, Policy-based methods can learn either stochastic or deterministic policies. With a stochastic policy, our neural network’s output is an action vector that represents a probability distribution (rather than returning a single deterministic action). The policy we will follow is selecting an action from this probability distribution. This means that if our agent ends up in the same state twice, we may not end up taking the same action every time.
尽管我们在上一篇文章中已经编码了确定性策略,但是基于策略的方法可以学习随机策略或确定性策略。 使用随机策略,我们的神经网络的输出是一个表示概率分布的作用向量(而不是返回单个确定性作用)。 我们将遵循的策略是从该概率分布中选择一个动作。 这意味着,如果我们的代理两次处于相同状态,则可能不会每次都采取相同的操作。
The key idea underlying policy gradients is reinforcing good actions: to push up the probabilities of actions that lead to higher return, and push down the probabilities of actions that lead to a lower return, until you arrive at the optimal policy. The policy gradient method will iteratively amend the policy network weights (with smooth updates) to make state-action pairs that resulted in positive return more likely, and make state-action pairs that resulted in negative return less likely.
政策梯度背后的关键思想是加强良好的行动:提高导致较高回报的行动的可能性,并降低导致较低回报的行动的可能性,直到您获得最佳策略为止。 策略梯度方法将迭代地修改策略网络权重(平滑更新),以使产生正收益的状态-动作对更有可能,而使产生负收益的状态-动作对更不可能。
From this post on, we will begin to enter into a more rigorous definition at a mathematical level of everything that we are presenting since it will be good for us to understand the most advanced algorithms. We will start describing the primary form of the REINFORCE algorithm ( original paper), the fundamental policy gradient algorithm on which nearly all the advanced policy gradient algorithms are based.
从这篇文章开始,我们将开始在数学上对我们所呈现的所有事物进行更严格的定义,因为这对我们理解最先进的算法将是一件好事。 我们将开始描述REINFORCE算法的主要形式( 原始论文 ),这是基本策略梯度算法,几乎所有高级策略梯度算法都基于该基本策略梯度算法。
数学定义 (Mathematical definitions)
弹道 (Trajectory)
The first thing we need to define is a trajectory, just a state-action sequence without keeping track of the rewards:
我们需要定义的第一件事是一条轨迹 ,只是一个状态-动作序列,而没有跟踪奖励:

A trajectory is a little bit more flexible than an episode because there are no restrictions on its length; it can correspond to a full episode or just a part of an episode.
轨迹比情节稍微灵活一点,因为它的长度没有限制。 它可以对应于整集或部分集。
We denote the length with a capital H, where H stands for Horizon, and we represent a trajectory with τ:
我们用大写字母H表示长度,其中H表示Horizon ,并且用τ表示轨迹:

The method is built upon trajectories instead of episodes because maximizing expected return over trajectories (instead of episodes) lets the method search for optimal policies for both episodic and continuing tasks.
该方法建立在轨迹而不是情节的基础上,因为最大化轨迹的预期收益(而不是情节)可以使该方法针对情景任务和连续任务搜索最佳策略。
Although for the vast majority of episodic tasks, where a reward is only delivered at the end of the episode, it only makes sense just to use the full episode as a trajectory; otherwise, we don’t have enough reward information to meaningfully estimate the expected return.
尽管对于大多数情节任务而言,奖励仅在情节结束时才提供,但仅将整个情节用作轨迹才有意义; 否则,我们没有足够的奖励信息来有意义地估计预期收益。
返回轨迹 (Return of a trajectory)
We denote the return for a trajectory τ with R(τ), and it is calculated as the sum reward from that trajectory τ:
我们用R(τ)表示轨迹τ的收益 , 并计算为该轨迹τ的总奖励:

预期收益 (Expected return)
Remember that the goal of this algorithm is to find the weights θ of the neural network that maximize expected return that we denote by U(θ) and can be defined as:
请记住,该算法的目标是找到使期望回报最大化的神经网络权重θ ,我们用U(θ)表示,可以定义为:

To see how it corresponds to the expected return, note that we have expressed the return R(τ) as a function of the trajectory τ. Then, we calculate the weighted average, where the weights are given by P(τ;θ), the probability of each possible trajectory, of all possible values that the return R(τ) can take. Note that probability depends on the weights θ in the neural network because θ defines the policy used to select the actions in the trajectory, which also plays a role in determining the states that the agent observes.
要查看它与预期收益如何对应,请注意,我们已将收益R ( τ )表示为轨迹τ的函数。 然后,我们计算加权平均值,其中权重为 P( τ ; θ ),即返回R ( τ )可以取的所有可能值的每个可能轨迹的概率。 请注意,概率取决于神经网络中的权重θ ,因为θ定义了用于选择轨迹中动作的策略,这在确定代理观察到的状态时也起着作用。
渐变上升 (Gradient ascent)
As we already introduced, one way to determine the value of θ that maximizes U(θ) function is through gradient ascent.
正如我们已经介绍的那样,确定使U(θ)函数最大化的θ值的一种方法是通过梯度上升 。
Gradient ascent is closely related to gradient descent, where the differences are that gradient descent is designed to find the minimum of a function (steps in the direction of the negative gradient), whereas gradient ascent will find the maximum (steps in the direction of the gradient).
梯度上升与梯度下降密切相关,区别在于梯度下降被设计为找到函数的最小值 (向负梯度的方向步进) ,而梯度上升将找到最大值(向负梯度的方向步进)。 渐变) 。
Equivalent to Hill Climbing algorithm presented in the previous Post, intuitively we can visualize that the gradient ascent draws up a strategy to reach the highest point of a hill, U(θ), just iteratively taking small steps in the direction of the gradient:
等效于上一篇文章中介绍的Hill Climbing算法,直观地我们可以直观地看到,梯度上升拟定了一种策略来达到山的最高点U(θ) ,只是在梯度方向上逐步采取了一些小步骤:

Mathematically, our update step for gradient ascent can be expressed as:
从数学上讲,我们对梯度上升的更新步骤可以表示为:

where α is the step size that is generally allowed to decay over time (equivalent to the learning rate decay in deep learning). Once we know how to calculate or estimate this gradient, we can repeatedly apply this update step, in the hopes that θ converges to the value that maximizes U(θ).
其中α是通常允许随时间衰减的步长(相当于深度学习中的学习速率衰减 )。 一旦知道了如何计算或估计该梯度,就可以重复应用此更新步骤,以期θ收敛到使U ( θ )最大化的值。
抽样与估算 (Sampling and estimate)
To apply this method, we will need to be able to calculate the gradient ∇U(θ); however, we won’t be able to calculate the exact value of the gradient since that is computationally too expensive because, to calculate the gradient exactly, we’ll have to consider every possible trajectory, becoming an intractable problem in most cases.
为了应用这种方法,我们将需要能够计算梯度∇U(θ); 但是,我们将无法计算梯度的确切值,因为这在计算上过于昂贵,因为要精确计算梯度,我们将必须考虑所有可能的轨迹,这在大多数情况下会成为棘手的问题。
Instead of doing this, the method samples a few trajectories using the policy and then use those trajectories only to estimate the gradient. This is equivalent to the approach of Monte Carlo presented in Post 13 of this series, and for this reason, method REINFORCE is also known as Monte Carlo Policy Gradients.
代替执行此操作,该方法使用策略对一些轨迹进行采样,然后仅将这些轨迹用于估计梯度。 这等效于本系列文章后13中介绍的蒙特卡洛方法,因此,REINFORCE方法也称为蒙特卡洛政策梯度。
伪码 (Pseudocode)
In summary, the described method is a loop that has three steps:
总之,所描述的方法是一个包含三个步骤的循环:
- Collect trajectories 收集轨迹
- Use the trajectories to estimate the gradient 使用轨迹估计坡度
- Update the weights of the policy 更新政策的权重
The pseudocode that describes in more detail the behavior of this method can be written as:
更详细地描述此方法的行为的伪代码可以写为:

梯度估算公式 (Gradient estimation formula)
As the reader can see in the equation of step 2 in the pseudocode, to estimate the gradient (which we will refer to as g hat for simplicity), the method uses these m trajectories collected in step 1. Let’s look a bit more closely at this equation. To understand it, we begin by making some simplifying assumptions, for example, assuming that we only have a single trajectory (m=1) that corresponds to a full episode. Then the equation for the gradient estimation looks like this:
正如读者在伪代码的步骤2的方程式中所看到的那样,为了估计梯度(为简单起见,我们将其称为g hat),该方法使用了在步骤1中收集的这m条轨迹。让我们更仔细地看一下这个方程式。 为了理解它,我们首先进行一些简化的假设,例如,假设我们只有一个与整个情节相对应的单个轨迹( m = 1)。 然后,用于梯度估计的公式如下所示:

Remember that R(τ) is just the cumulative reward from the trajectory τ, the only one trajectory in this simplified example. Assume that the reward signal and the sample play we are working with gives the Agent a reward of positive one (R(τ)=+1) if we won the game and a reward of negative one (R(τ)=-1) if we lost. In the other hand, the term
请记住, R ( τ )只是轨迹τ的累积奖励,在此简化示例中,轨迹τ是唯一的一条轨迹。 假设我们正在使用的奖励信号和示例游戏给Agent带来了正数的奖励( R ( τ )= + 1)(如果我们赢了游戏),而负数的奖励( R ( τ )=-1)。如果我们输了。 另一方面,术语

looks at the probability that the Agent selects action at from state st in time step t. Remember that π with the subscript θ refers to the policy which is parameterized by θ. Then, the full expression takes the gradient of the log of that probability is
着眼于概率代理选择从国家行动 ST在时间步长 吨 。 请记住,带有下标θ的 π 表示由θ参数化的策略。 然后,完整表达式采用该概率的对数的梯度

This will tell us how we should change the weights of the policy θ if we want to increase the log probability of selecting action at from state st. Specifically, suppose we nudge the policy weights by taking a small step in the direction of this gradient. In that case, it will increase the log probability of selecting the action from that state, and if we step in the opposite direction will decrease the log probability.
这将告诉我们,我们应该如何改变政策θ的权重,如果我们希望增加从国家选择动作的数概率 圣 具体来说,假设我们朝这个梯度的方向走了一小步,就可以轻推政策权重。 在那种情况下,它将增加从该状态选择动作的对数概率,而如果我们朝相反的方向迈进,则将降低对数概率。
The following equation will do all of these updates all at once for each state-action pair, at and st, at each time step t in the only trajectory:
下面的方程式将在唯一轨迹的每个时间步t处的每个状态动作对at和st一次完成所有这些更新:

To see this behavior, assume that the Agent won the episode. Then, R(τ) is just a positive one (+1), and what the sum does is add up all the gradient directions we should step in to increase the log probability of selecting each state-action pair. That’s equivalent to just taking H+1 simultaneous steps where each step corresponds to a state-action pair in the trajectory.
要查看此行为,请假定特工赢得了该集。 然后, R ( τ )只是一个正数(+1),总和就是将所有我们应该介入的梯度方向加起来,以增加选择每个状态-动作对的对数概率。 这等效于仅同时执行H + 1个步骤,其中每个步骤对应于轨迹中的状态-动作对。
In the opposite, if the Agent lost, R(τ) becomes a negative one, which ensures that instead of stepping in the direction of the steepest increase of the log probabilities, the method steps in the direction of the steepest decrease.
相反,如果Agent丢失,则R ( τ )变为负数,这确保了方法不是朝对数概率的最陡峭增加的方向步进,而是朝着最陡峭的减小方向步进。
Well, remember that this explanation was for a simplified example. In the general equation, you will notice that it is almost identical. We now need to add contributions from multiple trajectories (with the sum) and add a scaling factor that’s inversely proportional to the number of trajectories:
好吧,请记住,这种解释只是为了简化示例。 在一般等式中,您会注意到它几乎是相同的。 现在,我们需要添加来自多个轨迹(总和)的贡献,并添加与轨迹数量成反比的缩放因子:

If the reader wants to learn how to derive the equation that approximates the gradient, it can be found in the Post’s Appendix. However, this derivation can be safely skipped.
如果读者想学习如何推导近似梯度的方程,可以在《 邮报》附录中找到 。 但是,可以安全地跳过此推导。
为什么要优化对数概率而不是概率 (Why optimize log probability instead of probability)
In Gradient methods where we can formulate some probability 𝑝 which should be maximized, we would actually optimize the log probability log𝑝 instead of the probability for some parameters 𝜃.
在梯度方法中,我们可以制定应最大化的概率,,实际上,我们将优化对数概率log𝑝而不是某些参数the的概率。
The reason is that generally, work better to optimize log𝑝(𝑥) than 𝑝(𝑥) due to the gradient of log𝑝(𝑥) is generally more well-scaled. Remember that probabilities are bounded by 0 and 1 by definition, so the range of values that the optimizer can operate over is limited and small.
原因是通常,由于log𝑝(𝑥)的梯度通常更易于缩放 ,因此比log(𝑥)更好地优化log𝑝(𝑥)。 请记住,根据定义,概率受0和1限制,因此优化器可以操作的值的范围有限且很小。
In this case, sometimes probabilities may be extremely tiny or very close to 1, and this runs into numerical issues when optimizing on a computer with limited numerical precision. If we instead use a surrogate objective, namely log p (natural logarithm), we have an objective that has a larger “dynamic range” than raw probability space, since the log of probability space ranges from (-∞,0), and this makes the log probability easier to compute.
在这种情况下,有时概率可能极小或非常接近1,并且在数值精度有限的计算机上进行优化时会遇到数值问题。 如果我们改用替代目标,即log p (自然对数),则我们的目标“动态范围”比原始概率空间大,因为概率空间的对数范围为(-∞,0),并且使对数概率更易于计算。
编码加强 (Coding REINFORCE)
After describing the method mathematically, in this section, we will explore an implementation of the REINFORCE to solve OpenAI Gym’s Cartpole environment. To help the reader understand the essential parts, we implemented the simplified example where each trajectory corresponds to a full episode, and we collect only one (m=1) trajectory.
在数学上描述了方法之后,在本节中,我们将探索REINFORCE的实现以解决OpenAI Gym的Cartpole环境 。 为了帮助读者理解基本部分,我们实施了简化示例,其中每个轨迹对应一个完整的情节,并且我们仅收集一个( m = 1)轨迹。
The entire code of this post can be found on GitHub and can be run as a Colab google notebook using this link.
这篇文章的完整代码可以在GitHub上找到 , 也可以使用此链接作为Colab谷歌笔记本运行 。
Acknowledgments: The code presented in this post has been inspired by the REINFORCEMENT implementation shared at Udacity GitHub.
致谢:这篇文章中介绍的代码是受Udacity GitHub上共享的REINFORCEMENT实现的启发。
First, we will import all necessary packages with the following lines of code:
首先,我们将使用以下代码行导入所有必需的软件包:
import gymimport numpy as npfrom collections import dequeimport matplotlib.pyplot as pltimport torch
torch.manual_seed(0) # set random seedimport torch.nn as nnimport torch.nn.functional as Fimport torch.optim as optimfrom torch.distributions import CategoricalAnd also the OpenAI Gym’s Cartpole Environment:
还有OpenAI Gym的Cartpole环境:
env = gym.make('CartPole-v0')Next in the code, we define the policy π (and initialize it with random weights):
接下来,在代码中,我们定义策略π(并使用随机权重对其进行初始化):
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")class Policy(nn.Module):def __init__(self, s_size=4, h_size=16, a_size=2):
super(Policy, self).__init__()
self.fc1 = nn.Linear(s_size, h_size)
self.fc2 = nn.Linear(h_size, a_size) def forward(self, x):
x = F.relu(self.fc1(x))
x = self.fc2(x)return F.softmax(x, dim=1)def act(self, state):
state = torch.from_numpy(state).float()
.unsqueeze(0).to(device)
probs = self.forward(state).cpu()
m = Categorical(probs)
action = m.sample()return action.item(), m.log_prob(action)Two convolutional layers make the policy neural network:
两个卷积层构成了策略神经网络:
Policy(
(fc1): Linear(in_features=4, out_features=16, bias=True)
(fc2): Linear(in_features=16, out_features=2, bias=True)
)The code to train REINFORCE is similar to the code of Hill-Climbing method already described in the previous post:
到列车加强代码类似于已经描述的爬山方法的代码以前的帖子 :
policy = Policy().to(device)
optimizer = optim.Adam(policy.parameters(), lr=1e-2)def reinforce(n_episodes=10000, max_t=1000, gamma=1.0):
scores_deque = deque(maxlen=100)
scores = []for i_episode in range(1, n_episodes+1):
saved_log_probs = []
rewards = []
state = env.reset()for t in range(max_t):
action, log_prob = policy.act(state)
saved_log_probs.append(log_prob)
state, reward, done, _ = env.step(action)
rewards.append(reward)if done:break
scores_deque.append(sum(rewards))
scores.append(sum(rewards))
discounts = [gamma**i for i in range(len(rewards)+1)]
R = sum([a*b for a,b in zip(discounts, rewards)])
policy_loss = []for log_prob in saved_log_probs:
policy_loss.append(-log_prob * R)
policy_loss = torch.cat(policy_loss).sum()
optimizer.zero_grad()
policy_loss.backward()
optimizer.step()if i_episode % 100 == 0:
print('Episode {}\tAverage Score: {:.2f}'.format(i_episode, np.mean(scores_deque)))if np.mean(scores_deque)>=195.0:
print('Environment solved in {:d} episodes!\tAverage
Score: {:.2f}'.format(i_episode-100,
np.mean(scores_deque)))breakreturn scoresscores = reinforce()
We can plot the scores obtained in each episode during training:
我们可以标出训练期间每个情节中获得的分数:
fig = plt.figure()
plt.plot(np.arange(1, len(scores)+1), scores)
plt.ylabel('Score')
plt.xlabel('Episode #')
plt.show()
We render how the Agent applies the policy with the following code:
我们使用以下代码来呈现代理如何应用策略:
def watch_agent():
env = gym.make('CartPole-v0')
state = env.reset()
rewards = []
img = plt.imshow(env.render(mode='rgb_array'))for t in range(2000):
action, _ = policy.act(state)
img.set_data(env.render(mode='rgb_array'))
plt.axis('off')
display.display(plt.gcf())
display.clear_output(wait=True)
state, reward, done, _ = env.step(action)
rewards.append(reward)if done:
print("Reward:", sum([r for r in rewards]))break
env.close()watch_agent()
If you run the code in the Colab you will be able to see how the Agent handles the cart pole with a dynamic image.
如果您在Colab中运行代码,您将能够看到代理如何处理带有动态图像的手推车。
接下来是什么? (What is next?)
In this post, we have explained in detail the REINFORCE algorithm, and we have coded it. However, can REINFORCE be improved? In the following Post, we will go over ways to improve the REINFORCE algorithm. All of the improvements will be utilized and implemented in the PPO algorithm. See you in the next post!
在这篇文章中,我们详细解释了REINFORCE算法,并对其进行了编码。 但是,REINFORCE是否可以改善? 在下面的文章中,我们将探讨改进REINFORCE算法的方法。 所有改进将在PPO算法中使用和实现。 下篇再见!
附录:如何推导梯度方程 (APPENDIX: How to derive the gradient equation)
This appendix is a mathematical demonstration of the equation that approximate the gradient, presenting how to derive the gradient ∇U(θ):
本附录是方程近似的梯度,呈现如何导出梯度∇U(θ)的数学示范:

方法 (Approach)
First, we will start writing the gradient as the expected value
首先,我们将开始将梯度写为期望值

and from here, it becomes much easier to express the final formula that articulates its approximation with the empirical estimate with a sample-based average of m trajectories under the policy.
从这里开始,用该策略在m个轨迹的基于样本的平均数下,用经验估计值表达表达其近似值的最终公式变得容易得多。
It is common to refer to this gradient as the likelihood ratio policy gradient, keystone to the method that performs a (stochastic) gradient ascent over the policy parameter space to find a local optimum of U(θ).
通常将此梯度称为似然比策略梯度,这是在策略参数空间上执行(随机)梯度上升以找到U(θ)局部最优值的方法的基石。
似然比政策梯度 (Likelihood Ratio Policy Gradient)
In order to obtain the likelihood ratio policy gradient, we start from
为了获得似然比策略梯度,我们从

and taken the gradient of both sides we obtain a first expression of its value:
并采用双方的渐变,我们得到其值的第一个表达式:

We can then get this formula and rewrite the gradient of the sum as the sum of the gradients
然后,我们可以获取此公式并将总和的梯度重写为梯度的总和

If we multiply every term in the sum by this factor
如果我们将总和中的每一项乘以这个因子

which is perfectly allowed because this fraction is equal to one, we have this expression
这是完全允许的,因为这个分数等于1,我们有这个表达式

and with a simple rearrangement of the terms, we obtain
并通过简单地重新排列术语,我们获得

Now, if we consider the chain rule, and the fact that the gradient of the log of a function is always equal to the gradient of the function, divided by the function
现在,如果考虑链式规则,以及函数对数的斜率始终等于函数的斜率除以函数的事实

we obtain the expected formula for the likelihood ratio policy gradient
我们获得似然比策略梯度的期望公式

Once we have written the gradient as an expected value in this way, it becomes much easier to estimate.
通过这种方式将梯度写为期望值后,估计起来就容易得多了。
抽样与估算 (Sampling and estimate)
We already introduced that we won’t be able to calculate the exact value of the gradient ∇U(θ) since that is computationally too expensive, because to calculate the gradient exactly, we’ll have to consider every possible trajectory, becoming an intractable problem in most cases. Instead of doing this, the method samples a few trajectories using the policy and then use those trajectories only to estimate the gradient.
我们已经介绍了,我们将不能够计算梯度∇U(θ),因为这是计算过于昂贵的精确值,因为精确地计算梯度,我们必须要考虑每一个可能的轨迹,成为在大多数情况下都是棘手的问题。 代替执行此操作,该方法使用策略对一些轨迹进行采样,然后仅将这些轨迹用于估计梯度。
For doing that, we can approximate the likelihood ratio policy gradient with a sample-based average, as shown below:
为此,我们可以使用基于样本的平均值来近似似然比策略梯度,如下所示:

The best way to proceed to get the desired expression for the likelihood ratio policy gradient is to simplify
继续为似然比策略梯度获得所需表达式的最佳方法是简化
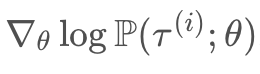
We will start with unrolling the expression of the probability of a trajectory taking into account the action-selection probabilities from the policy
我们将从考虑策略中的动作选择概率展开轨迹概率的表达开始

and take the gradient of both sides we obtain a first expression of the its value:
并取两边的梯度,我们得到其值的第一个表达式:

Then, because the log of a product is equal to the sum of the logs, we obtain the following expression:
然后,由于一个产品的对数等于该对数的总和,因此我们获得以下表达式:

Because the gradient of the sum can be written as the sum of gradients, this is equal to
因为总和的梯度可以写成梯度的总和,所以等于

The first component of this expression
此表达式的第一部分

has no dependence on θ, so
与θ无关

and this implies that
这意味着

Finally, because we can rewrite the gradient of the sum as the sum of gradients, we obtain the desired function
最后,因为我们可以将和的梯度重写为梯度的和,所以我们获得了所需的函数

And from here, replacing the previous calculation in the formula that approximate the likelihood ratio policy gradient with a sample-based average
然后从此处开始,用基于样本的平均值替换近似似然比策略梯度的公式中的先前计算

we obtain the final equation to estimate the gradient
我们得到最终方程来估计梯度

翻译自: https://towardsdatascience.com/policy-gradient-methods-104c783251e0
梯度下降法 梯度上升法







 本文介绍了梯度下降法和梯度上升法,并重点讲解了在深度学习中政策梯度方法的应用。通过翻译自的数据科学文章,读者可以深入理解这两种优化算法在人工智能和机器学习领域的实践。
本文介绍了梯度下降法和梯度上升法,并重点讲解了在深度学习中政策梯度方法的应用。通过翻译自的数据科学文章,读者可以深入理解这两种优化算法在人工智能和机器学习领域的实践。














 949
949

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








