javascript计算器_JavaScript问题解决器：计算否定项

最新推荐文章于 2022-08-18 16:42:20 发布

weixin_26738395

最新推荐文章于 2022-08-18 16:42:20 发布

阅读量278

点赞数

文章标签： python java javascript leetcode 算法 ViewUI

原文链接：https://levelup.gitconnected.com/javascript-problem-solvers-count-negatives-bd182f609551

版权

javascript计算器

This week, we are returning back to matrices because they are so fun. Just so much fun.

本周，我们将返回矩阵，因为它们是如此有趣。太有趣了。

The problem at hand isn't as difficult as problems we’ve solved before like Rotate Image Matrix or Minimum Time Visiting All Points, but still provides a good exercise on different ways you can work through data within a 2D matrix.

眼前的问题并不像我们之前解决的问题那样困难，例如“ Rotate Image Matrix或Minimum Time Visiting All Points ，但仍然可以很好地练习如何处理2D矩阵中的数据。

So, let’s get solving.

所以，让我们解决。

问题 (THE PROBLEM)

Here is a link to the problem on LeetCode

这是有关LeetCode问题的链接

Given a m * n matrix grid which is sorted in non-increasing order both row-wise and column-wise.Return the number of negative numbers in grid.

约束 (THE CONSTRAINTS)

The constraints we get are your standard thoroughfare of constraints for problems dealing with 2D matrices. At this point, they are what we have come to expect. But as always, it’s a good idea to go through each constraint to make sure we know what we are dealing with:

我们得到的约束是您处理2D矩阵问题时的标准约束的全面说明。在这一点上，它们就是我们所期望的。但是与往常一样，最好通过每个约束条件来确保我们知道我们要处理的内容：

m == grid.length

Since we are being given an m * n matrix grid, the amount of rows and columns in a given matrix are linearly independent. We could have more rows than columns, and we could have more columns than rows. m represents the amount of rows we should expect for any given matrix.

由于我们得到的是m * n矩阵grid ，因此给定矩阵中的行和列的数量是线性独立的。我们可以有比列更多的行，并且我们可以有比行更多的列。 m表示对于任何给定矩阵我们应该期望的行数。

n == grid[i].length

n represents the amount of columns we should expect. Nothing out of the ordinary here either.

n表示我们应该期望的列数。这里也没有什么不寻常的。

1 <= m, n <= 100

Here we get an upper limit and a lower limit for how many rows or columns we should expect to see. With a lower limit of 1 <=, we can can rely on the fact that wont have to worry about handling empty rows or columns. The upper limit is not as essential, but should we want to come up with some custom test cases, the upper limit of <= 100 gives us enough information to do so.

在这里，我们获得了应该看到的行数或列数的上限和下限。下限为1 <= ，我们可以依靠这样的事实：不必担心处理空的行或列。上限不是必需的，但是如果我们想提出一些自定义测试用例，则上限<= 100为我们提供足够的信息。

-100 <= grid[i][j] <= 100

grid[i][j] represents each element in the matrix, and this constraint gives us an upper and lower limit for each element. Since this is a problem strictly dealing with the values of each element and whether or not an element is a negative number, the lower limit of -100 <= makes complete sense, as does the upper limit of <= 100. It is good to know we won’t be having to handle any really big numbers.

grid[i][j]代表矩阵中的每个元素，该约束为我们提供了每个元素的上限和下限。由于严格地处理每个元素的值以及元素是否为负数是一个问题，因此-100 <=的下限和<= 100的上限完全有意义。很高兴知道我们将不必处理任何真正大的数字。

测试 (THE TESTS)

Test Case #1:


Input: grid = [[4,3,2,-1],[3,2,1,-1],[1,1,-1,-2],[-1,-1,-2,-3]]
Output: 8


Explanation: There are 8 negatives number in the matrix.


~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~


Test Case #2:


Input: grid = [[3,2],[1,0]]
Output: 0


~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Test Case #3:


Input: grid = [[1,-1],[-1,-1]]
Output: 3


~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~


Test Case #4:


Input: grid = [[-1]]
Output: 1


~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

崩溃 (THE BREAK DOWN)

The problem’s explanation and scope is fairly simple, though might prove to have a few tricks up it’s sleeve. So, as usually, let’s breakdown each line of the problem’s explanation, look for any clues that might lead us to a solution, and make sure we understand what we are tasked with solving:

问题的解释和范围很简单，尽管可能会证明有些窍门。因此，像往常一样，让我们细分问题的解释的每一行，寻找可能导致我们找到解决方案的任何线索，并确保我们了解要解决的任务：

Given a m * n matrix grid which is sorted in non-increasing order both row-wise and column-wise.

Straight and to the point. Just the way I like it. Let’s break this first part down even further as we have been given a lot of information in a single sentence:

直截了当。就是我喜欢的方式。让我们进一步分解第一部分，因为我们在一个句子中获得了很多信息：

Given a m * n matrix grid

Given a m * n matrix grid simply means the amount of rows and columns in a given matrix are independent from one another. This secretly tells me that even though some of our test cases might have an equal number of rows and columns, others might not, and we can’t iterate through rows and columns at the same time. If we want to do so, we will have to find a different solution.

Given am * n matrix grid仅表示给定矩阵中的行和列的数量彼此独立。这秘密告诉我，即使我们的一些测试用例可能具有相同数量的行和列，而其他测试用例可能没有，并且我们不能同时遍历行和列。如果我们想这样做，我们将不得不寻找其他解决方案。

sorted in non-increasing order

sorted in non-increasing order is another way of saying sorted in a decreasing order, which is another way of saying “The numbers keep getting smaller.” This helps a lot, and tells me that we don’t have to worry about coming up with a way to sort elements in grid or grid[i]. The work is already done for us.

sorted in non-increasing order是另一种以sorted in a decreasing order的说法，这是另一种说法“数字越来越小”。 这很有帮助，并告诉我，我们不必担心想出对grid或grid[i]元素进行排序的方法。该工作已经为我们完成。

both row-wise and column-wise

This is even more helpful than having elements in a non-increasing order. Not only is each row sorted, but each column is sorted as well. This means the first element in the matrix will always be the largest number in the entire matrix, and the last number in the matrix will always be the smallest (or most negative) number in the entire matrix.

这比以不递增的顺序排列元素更有帮助。不仅对每一行进行排序，而且对每一列也进行排序。这意味着矩阵中的第一个元素将始终是整个矩阵中最大的数字，而矩阵中的最后一个元素将始终是整个矩阵中最小(或最大负数)的数字。

If we look at Test Case #1, we can see this for ourselves:

如果我们看一下测试用例1，我们可以自己看到：

[ 4, 3, 2, -1]
[ 3, 2, 1, -1]
[ 1, 1,-1, -2]
[-1,-1,-2,-3]

〜

Return the number of negative numbers in grid.

Here is our task in a nutshell. We need to figure out an efficient way to iterate through a given matrix, and determine if an element is negative or positive.

简而言之，这是我们的任务。我们需要找出一种有效的方法来遍历给定的矩阵，并确定元素是负还是正。

怀疑 (THE SUSPECTS)

I came up with two different yet similar solutions: one with a nested loop, and one with a flattened matrix. Both of which will iterate through grid in a unique fashion, yet still produce the results we are looking for.

我想出了两种不同但又相似的解决方案：一种具有嵌套循环，另一种具有扁平矩阵。两者都将以独特的方式遍历grid ，但仍会产生我们所寻找的结果。

Since we need to determine if a number is negative, we can use Math.sign(). Math.sign() will return 1 if a number is positive, 0 if a number is zero, and -1 if a number is negative.

由于我们需要确定数字是否为负数，因此可以使用Math.sign() 。如果数字为正， Math.sign()将return 1；如果数字为零，则return 0；如果数字为负，则return -1。

We also need to return the amount of negative numbers in a matrix, and we can keep track of that with a counter variable.

我们还需要return矩阵中的负数，并且我们可以使用计数器变量来跟踪它。

But all we care about is if a number is negative. 0 and positive numbers don’t matter. So, if Math.sign(<a number>) === -1, we increment the counter.

但是我们只关心数字是否为负数。 0和正数无关紧要。因此，如果Math.sign(<a number>) === -1 ，我们将增加计数器。

That is where the similarities for our two solutions end. With our task being fairly simple, we can turn our attention to figuring out an effective way to iterate through a given matrix.

这就是我们两个解决方案的相似之处。由于我们的任务相当简单，因此我们可以将注意力转移到寻找一种有效方法来迭代给定矩阵。

There are two approaches we can take:

我们可以采用两种方法：

Solution #1: Backwards Nested Iteration

解决方案1：向后嵌套迭代

If we do not want to mutate grid, we can use the order of a given matrix to our advantage. Since grid is sorted in a non-increasing order both row-wise and column wise, we can iterate through each sub array of grid starting from the last element in grid. That is where we are most likely to find a sub-array with negative numbers in it. We can also start with the last element in each sub array grid[i][j] since that is where it is most likely we will find a negative number as well.

如果我们不想改变grid ，我们可以利用给定矩阵的阶数来获得优势。由于grid是在非增顺序排序都行方向和列明智的，我们可以通过的每个子阵列进行迭代grid从在最后元素开始grid 。那就是我们最有可能找到其中带有负数的子数组的地方。我们也可以从每个子数组grid[i][j]的最后一个元素开始，因为那是最有可能找到负数的地方。

Starting at the end of grid, and at the end of grid[i], we can iterate through grid[i] and check if Math.sign(grid[i][j]) === -1 and if so, increment our counter.

从grid的末尾开始，并在grid[i]的末尾，我们可以遍历grid[i]并检查Math.sign(grid[i][j]) === -1 ，如果是，则递增我们的柜台。

If Math.sign(grid[i][j]) !== -1, then grid[i][j] must be a positive number (or 0), and since grid[i] is sorted in non-increasing order, we wont find anymore negative numbers in grid[i] and the rest of the sub array must be filled with positive numbers.

如果Math.sign(grid[i][j]) !== -1 ，则grid[i][j]必须为正数(或0)，并且由于grid[i]以非递增顺序排序，我们将在grid[i]再也找不到负数，并且子数组的其余部分必须用正数填充。

Once Math.sign(grid[i][j]) !== -1, we can break out of the iteration.

一旦Math.sign(grid[i][j]) !== -1 ，我们就可以退出迭代。

The only problem with this solution is we would need to nest an iteration to access grid[i][j], and in the worst case scenario, it would run in O(n²) time.

此解决方案的唯一问题是，我们将需要嵌套一个迭代来访问grid[i][j] ，在最坏的情况下，它将在O(n²)时间内运行。

I think we can do better.

我认为我们可以做得更好。

Solution #2: Flattened Single Iteration

解决方案2：扁平化单迭代

So the non-increasing order of grid only matters in the context of rows and columns. Well, since all we need to do is determine if a number is negative, the order doesn’t really matter. What if we threw out all the rows and columns and just flattened the matrix?

因此， grid的非递增顺序仅在行和列的上下文中才重要。好吧，由于我们所需要做的就是确定一个数字是否为负，所以顺序并不重要。如果我们将所有行和列都扔掉，然后将矩阵展平怎么办？

If we flatten grid and set the flattened matrix to a variable called something like flatGrid, we can use a single iteration to loop through flatGrid and run the same if statement as we did in the first solution. That does mean we would need to check each element without being able to break out of the iteration.

如果我们将grid展平并将其展平的矩阵设置为诸如flatGrid类的变量，则可以使用一次迭代遍历flatGrid并运行与第一个解决方案相同的if语句。那确实意味着我们将需要检查每个元素而又不能中断迭代。

We could sort flatGrid, but if we call .sort() on flatGrid in order to do so, we would actually increase our time complexity since .sort() generally uses Merge and Quick sort methods depending on your runtime environment. Both methods generally running in O(n log n) time, though Merge sort would end up running in O(n²) time if flatGrid starts getting large.

我们可以对flatGrid排序，但是如果要在flatGrid上调用.sort() ，则实际上会增加时间复杂度，因为.sort()通常根据您的运行时环境使用Merge和Quick排序方法。两种方法通常都在O(n log n)时间运行，但是如果flatGrid开始变大，合并排序最终将在O(n²)时间运行。

So it would actually be faster for us to iterate through the unsorted flattened array given our constraint 1 <= m, n <= 100.

因此，在给定约束1 <= m, n <= 100对我们而言，遍历未排序的平坦数组实际上会更快。

We can also use [].concat.apply([], grid) instead of grid.flat() as it is a more effective way of flattening an array when we don’t know the length of an array beforehand.

我们也可以使用[].concat.apply([], grid)代替grid.flat()因为当我们事先不知道数组的长度时，这是一种更有效的扁平化数组的方法。

伪代码 (THE PSEUDO CODE)

Now that we have worked through a couple solutions, lets try writing some pseudo code before putting anything to code:

现在我们已经完成了几个解决方案，让我们先尝试编写一些伪代码，然后再将任何内容添加到代码中：

Solution #1: Backwards Nested Iteration

解决方案1：向后嵌套迭代

// Solution #1: Backwards Nested Iteration


// - define a variable count to keep track of the amount of negative numbers in grid
//   - count = 0


// - define a for loop to iterate through grid that starts at the last element in grid
//   - i = grid.length - 1, i >= 0, i--


//   - define a nested for loop to iterate through grid[i] that starts at the last element in grid[i]
//     - j = grid[i].length - 1, j >= 0, j--


//    - use Math.sign() for each element grid[i][j] to determine if a number is negative
//      - Math.sign(grid[i][j]) === -1


//    - if so, increment the count variable
//        - count++


//    - otherwise, break out of the iteration
//      - else
//        - break


// - return the amount of negative numbers in grid
//   - return count

Solution #2: Flattened Single Iteration

解决方案2：扁平化单迭代

// Solution #2: Flattened Single Iteration


// - define a variable count to keep track of the amount of negative numbers in grid
//   - count = 0


// - define a variable flatGrid that flattens grid without using .flat()
//   - flatGrid = [].concat.apply([], grid)


// - define a for in loop that iterates through flatGrid
//   - num in flatGrid


//   - use Math.sign() for each element flatGrid[num] to determine if a number is negative
//    - Math.sign(flatGrid[num]) === -1


//   - if so, increment the count variable
//    - count++


// - return the amount of negative numbers in grid
//   - return count

Nice.

真好

代码 (THE CODE)

Now that we have worked out how both of our solutions should function, let’s see if they work:

现在我们已经确定了两种解决方案应如何工作，让我们看看它们是否有效：

Solution #1: Backwards Nested Iteration

解决方案1：向后嵌套迭代

First, let’s define our counter variable, count:

首先，让我们定义计数器变量count ：

var countNegatives = function(grid) {


// - define a variable count to keep track of the amount of negative numbers in grid
  let count = 0


};

Next, let’s set up our two for loops. Both of which starting at the end of grid and grid[i] respectively:

接下来，让我们设置两个for循环。两者都分别从grid和grid[i]的末尾开始：

var countNegatives = function(grid) {


  let count = 0


  // define a for loop to iterate through grid that starts at the last element in grid
  for(i = grid.length - 1; i >= 0; i--){


    // define a nested for loop to iterate through grid[i] that starts at the last element in grid[i]
    for(j = grid[i].length - 1; j >= 0; j--){


    }
  }


};

Then, all we need to do is add the logic that checks if a number is negative, increments count if it does, and breaks out of the iteration if it doesn’t:

然后，我们要做的就是添加逻辑，该逻辑检查数字是否为负，如果为负，则增加count如果不为负，则退出迭代：

var countNegatives = function(grid) {


  let count = 0


  for(i = grid.length - 1; i >= 0; i--){
    for(j = grid[i].length - 1; j >= 0; j--){


      // use Math.sign() for each element grid[i][j] to determine if a number is negative
      // if so, increment the count variable
      if(Math.sign(grid[i][j]) === -1) {
        count++


      // otherwise, break out of the iteration
      } else {
        break
      }
    }
  }


};

Finally, let’s add our return value:

最后，让我们添加return值：

var countNegatives = function(grid) {


  let count = 0


  for(i = grid.length - 1; i >= 0; i--){
    for(j = grid[i].length - 1; j >= 0; j--){
      if(Math.sign(grid[i][j]) === -1) {
        count++
      } else {
        break
      }
    }
  }


  // return the amount of negative numbers in grid
  return count
};

Let’s see if it works:

让我们看看它是否有效：

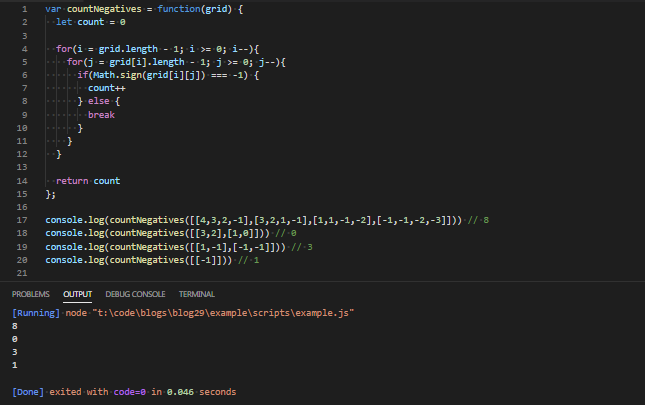
Nice.

真好

Solution #2: Flattened Single Iteration

解决方案2：扁平化单迭代

Once again, let’s define out count variable, as well as our flattened grid variable flatGrid:

再一次，让我们定义出count变量，以及我们展平的grid变量flatGrid ：

var countNegatives = function(grid) {


  // define a variable count to keep track of the amount of negative numbers in grid
  let count = 0


  // define a variable flatGrid that flattens grid without using .flat()
  const flatGrid = [].concat.apply([], grid)


};

Next, let’s setup our for in loop to iterate through flatGrid:

接下来，让我们设置for in循环遍历flatGrid ：

var countNegatives = function(grid) {


  let count = 0
  const flatGrid = [].concat.apply([], grid)


  // define a for in loop that iterates through flatGrid
  for(num in flatGrid){


  }




};

Then we can add the same logic that checks if a number is negative and increments count from the first solution:

然后，我们可以添加相同的逻辑来检查数字是否为负数，并从第一个解决方案开始递增count ：

var countNegatives = function(grid) {


  let count = 0
  const flatGrid = [].concat.apply([], grid)


  for(num in flatGrid){


    // use Math.sign() for each element flatGrid[num] to determine if a number is negative
    // if so, increment the count variable
    if(Math.sign(flatGrid[num]) === -1) {
      count++
    }
  }


};

Finally, we can add our return value:

最后，我们可以添加return值：

var countNegatives = function(grid) {


  let count = 0
  const flatGrid = [].concat.apply([], grid)


  for(num in flatGrid){
    if(Math.sign(flatGrid[num]) === -1) {
      count++
    }
  }


  // return the amount of negative numbers in grid
  return count
};

Let’s see if this works too:

让我们看看这是否也可行：

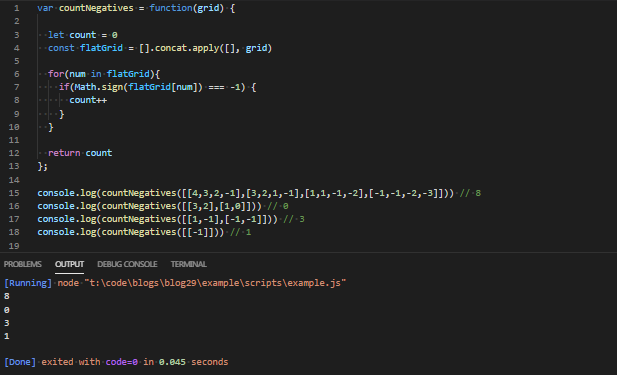
Nice.

真好

最终解决方案 (THE FINAL SOLUTIONS)

Let’s take a final look at our solutions without the comments, and clean up some of our syntax:

让我们最后看一下不带注释的解决方案，并清理一些语法：

Solution #1: Backwards Nested Iteration

解决方案1：向后嵌套迭代

var countNegatives = function(grid) {
  let count = 0
  for(i = grid.length - 1; i >= 0; i--){
    for(j = grid[i].length - 1; j >= 0; j--){
      if(Math.sign(grid[i][j]) === -1) count++
      else break
    }
  }
  return count
};

Solution #2: Flattened Single Iteration

解决方案2：扁平化单迭代

var countNegatives = function(grid) {
  let count = 0
  const flatGrid = [].concat.apply([], grid)
  for(num in flatGrid){ if(Math.sign(flatGrid[num]) === -1) count++ }
  return count
};

Nice.

真好

任务完成 (MISSION COMPLETE)

While countNegatives is not the most difficult or complex problem out there, I thought both solutions we came up with were different and interesting enough to warrant a blog about solving the countNegatives problem.

尽管countNegatives并不是目前最困难或最复杂的问题，但我认为我们提出的两种解决方案都是不同且有趣的，足以使我们countNegatives博客来解决countNegatives问题。

I definitely understand my solutions won’t be the best or most efficient, but I hope they help you or someone else figure out a way to solve a problem you encounter on this journey we call JavaScript.

我绝对知道我的解决方案不是最佳或最有效的，但希望它们能帮助您或其他人找出解决您在我们称为JavaScript的过程中遇到的问题的方法。

Either way, I hope you got some useful information, may all your functions return true, and all your requests respond with 200.

无论哪种方式，我都希望您能获得一些有用的信息，也许您所有的函数都返回true，并且所有请求均以200响应。

Stay safe…stay healthy…and keep fighting the good fight.

保持安全……保持健康……并继续打好仗。