数字三角形与算法-CSDN博客

数字三角形

In programming, the series that correspond to the triangular numbers seem to occur quite often. In this short story, I would like to discuss it a little with a couple fun algorithms to give some intuitions behind it.

在编程中，与三角数相对应的级数似乎经常出现。在这个简短的故事中，我想用一些有趣的算法对其进行一些讨论，以给出一些直观的认识。

I think most people have seen the triangular numbers at some point, they are the results of the following series:

我认为大多数人在某些时候都已经看到了三角形数字，它们是以下系列的结果：

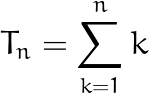
As you can see, it is quite simple. I remember the first time I learned it was in middle school, it is usually written more casually like this:

如您所见，这非常简单。我记得第一次上中学的时候，通常写得比较随意：

封闭式 (Closed Form)

as you may have guessed, this series has a closed form that’s quite easy to remember:

正如您可能已经猜到的那样，本系列的封闭形式很容易记住：

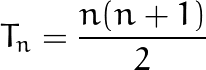
expanding it:

扩展它：

As you can see it is of order O(n²), many algorithms reduce down to the triangular numbers in performance, for example bubble sort, thus are of order n².

正如您所看到的，它的阶次为O(n²)，许多算法在性能上会降低到三角数，例如冒泡排序，因此为n²阶。

How do you arrive at this closed form?

您如何得出此封闭表格？

I still remember clearly how my teacher explained it. Suppose you have a series with even number of entries:

我仍然清楚地记得老师的解释。假设您有一个条目数偶数的序列：

how do you find its sum? Well, obviously you can just add them up one by one, but there is a shortcut. What if you pair up the numbers?

您如何找到它的总和？好吧，显然您可以将它们一个接一个地添加，但是有一个快捷方式。如果您将数字配对怎么办？

as you can see there are 3 pairs, and all of them sum to 7, since you have 6 entries that’s:

如您所见，有3对，并且它们全部加起来为7，因为您有6个条目，它们是：

So this is how you arrive at the closed form.

这就是您得出封闭表格的方式。

等边三角形 (Equilateral Triangles)

Let’s take look at the sums for each n:

让我们看一下每个n的总和：

if you draw them out as spheres arranged in equilateral triangles, they are the sizes of the equilateral triangles:

如果将它们绘制为以等边三角形排列的球体，则它们是等边三角形的尺寸：

Here is a short algorithm to generate these triangles in python:

这是在python中生成这些三角形的简短算法：

def create_triangles(n, res):

    if n <= 1:
        triangle = [['*']]
        res.append(triangle)
        return triangle

    row = ['*'] * n

    triangle = [row] + create_triangles(n - 1, res)

    res.append(triangle)
    return triangle


def start_create_triangles(n):

    res = []
    create_triangles(n, res)

    return resres = start_create_triangles(4)
for triangle in res:
    for row in reversed(triangle):
        print(row)

    print('')'''
['*']['*']
['*', '*']['*']
['*', '*']
['*', '*', '*']['*']
['*', '*']
['*', '*', '*']
['*', '*', '*', '*']
'''

For such short piece of code, we have used two techniques: recursion and global variable.

对于这么短的代码，我们使用了两种技术：递归和全局变量。

Triangular numbers correspond to the Faulhaber’s formula of the 1st power.

三角数对应于Faulhaber的一阶幂公式。

达成目标的步骤 (Steps to Reach Target)

Here is an interesting puzzle involving the triangular numbers:

这是一个涉及三角数的有趣难题：

If I stand at the origin, and there is a target somewhere on the positive axis, say, 6, and I want to reach the target.

如果我站在原点，并且在正轴上某处有一个目标，例如6，我想达到目标。

Every time I take a step, the size of the step corresponds to the nth time I take steps, so the first step I take is length 1, the second step is length 2, and so on.

每次执行步骤时，步骤的大小对应于执行步骤的第n次，因此我执行的第一步是长度1，第二步是长度2，依此类推。

The steps can be forwards or backwards, so the steps can be positive(+) or negative(-).

步长可以是向前或向后，因此步长可以为正(+)或负(-)。

The question is what is the minimum number of steps I need to take to reach my target.

问题是要达到目标我最少需要采取多少步骤。

解决 (Solve)

the first example is simple, the target we want to reach is 6. All we need to do is take steps:1, 2, 3. That sums up to 6.

第一个例子很简单，我们要达到的目标是6。我们要做的只是采取步骤：1、2、3。总计为6。

But what if the target we want to reach is 11?

但是，如果我们要达到的目标是11，该怎么办？

Can we reach it in 4 steps?

我们可以分四个步骤达到吗？

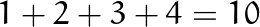
No way, even if all steps are toward the target, the maximum we can reach is 10, so we need more steps.

即使所有步骤都朝目标迈进，我们也无法达到最大值10，所以我们需要更多步骤。

How about 5 steps?

5个步骤怎么样？

Well, in this case, you can definitely walk past the target…

好吧，在这种情况下，您绝对可以走过目标……

So we need to think of a way to walk just enough to reach the target. Say, what if we take the first step backward?

因此，我们需要考虑一种步行方式，足以达到目标。说，如果我们向后迈出第一步怎么办？

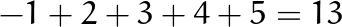
That’s still not enough, how about we take the second step backward instead?

那还不够，我们又往后退第二步呢？

Ah, just right!

啊，正好！

So, how do we generalize this process? Well, one thing to notice is this:

那么，我们如何概括这个过程？好，要注意的一件事是：

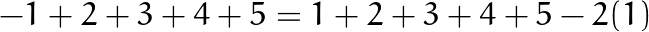
you see, whenever you decide to take a step backward, you are subtracting 2 times the size of that step from the triangular number. Therefore, the target can only be reached from a certain number of steps if the difference between the triangular number corresponding to that number of steps and the target is an even number!

您会看到，每当您决定向后退一步时，就会从三角数中减去该步大小的2倍。 因此，如果对应于该步数的三角形数与目标之间的差为偶数，则只能从一定步数达到目标！

So this gives a very good criteria to test whether a number of steps (or a triangular number) can reach the target:

因此，这提供了一个很好的标准来测试是否可以达到目标的步骤数(或三角形数)：

the sum of the steps (triangular number) has to be at least as large as the target.
步骤的总和(三角数)必须至少与目标一样大。
the difference between the target and the sum of the steps has to be even.
目标与步骤总和之间的差异必须相等。

Now we can implement our algorithm:

现在我们可以实现我们的算法：

def min_steps(target):

    res = 0
    sum = 0
    while sum < target or (sum - target) % 2 == 1:
        res = res + 1
        sum = sum + res

    return resmin_steps(11)
# 5

Works!

作品！