机器学习算法优缺点_用于机器学习的优化算法的优缺点-CSDN博客

本文探讨了用于机器学习的优化算法的强项和局限性，涵盖了各种算法在解决复杂问题时的表现，旨在帮助读者理解如何选择合适的算法来提升模型性能。

摘要由CSDN通过智能技术生成

机器学习算法优缺点

A deep-dive into Gradient Descent and other optimization algorithms

深入研究梯度下降和其他优化算法

Optimization Algorithms for machine learning are often used as a black box. We will study some popular algorithms and try to understand the circumstances under which they perform the best.

机器学习的优化算法通常被用作黑匣子。我们将研究一些流行的算法，并尝试了解它们在何种情况下表现最佳。

该博客的目的是： (The purpose of this blog is to:)

Understand Gradient descent and its variants, such as Momentum, Adagrad, RMSProp, NAG, and Adam;
了解梯度下降及其变体，例如动量，Adagrad，RMSProp，NAG和Adam。
Introduce techniques to improve the performance of Gradient descent; and
引入技术以改善梯度下降的性能；和
Summarize the advantages and disadvantages of various optimization techniques.
总结了各种优化技术的优缺点。

Hopefully, by the end of this read, you will find yourself equipped with intuitions towards the behavior of different algorithms, and when to use them.

希望在阅读本文结束时，您会发现自己对不同算法的行为以及何时使用它们具有直觉。

梯度下降 (Gradient descent)

Gradient descent is a way to minimize an objective function J(w),by updating parameters(w) in opposite direction of the gradient of the objective function. The learning rate η determines the size of the steps that we take to reach a minimum value of objective function.

梯度下降是一种通过在目标函数梯度的相反方向上更新参数(w)来最小化目标函数J(w)的方法。学习率η决定了达到目标函数最小值的步长。

Advantages and Disadvantages of Gradient Descent:

梯度下降的优点和缺点：

Overall Drawbacks of Gradient Descent:

梯度下降的总体缺点：

Techniques to improve the performance of Gradient Descent:

改善梯度下降性能的技术：

梯度下降的变化 (Variations of Gradient Descent)

Momentum
动量
Nesterov Accelerated Gradient
Nesterov加速梯度
Adagrad
阿达格勒
Adadelta/RMSProp
Adadelta / RMSProp
Adam
亚当

动量 (Momentum)

SGD (Stochastic Gradient Descent)has trouble navigating areas where the surface of optimization function curves much more steeply into one dimension than in another.

SGD(随机梯度下降)在导航区域中存在麻烦，在这些区域中，优化功能的曲面向一维弯曲的幅度比向一维弯曲的幅度大得多。

Momentum is a method that helps to accelerate SGD in the relevant direction, and dampens oscillations as can be seen below. It does this by adding a fraction using γ. γ is based on the principle of exponentially weighed averages, where weights are not drastically impacted by a single data point.

动量是一种有助于在相关方向上加速SGD并抑制振荡的方法，如下所示。通过使用γ加一个分数来实现。 γ基于指数加权平均值的原理，其中权重不受单个数据点的影响很大。

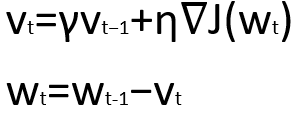
The momentum term increases in dimensions whose gradient continues in the same direction, and reduces updates for dimensions whose gradients change directions. As a result, we get faster convergence and reduced oscillation.

动量项增加了其梯度在相同方向上连续的尺寸，并减少了其梯度改变方向的尺寸的更新。结果，我们获得了更快的收敛速度并减少了振荡。

Nesterov加速梯度(NAG) (Nesterov accelerated gradient(NAG))

Nesterov accelerated gradient (NAG) is a way to give momentum more precision.

Nesterov加速梯度(NAG)是提高动量精度的一种方法。

We will use momentum to move the parameters. However, computing our parameters as shown below, gives us an approximation of the the gradient at the next position. We can now effectively look ahead by calculating the gradient not w.r.t. to our current value of the parameters but w.r.t. the approximate future value of the parameters.

我们将使用动量来移动参数。但是，如下所示计算参数，可以得出下一个位置处的梯度的近似值。现在，我们可以通过计算梯度(而不是参数的当前值)，而是计算参数的近似未来值，来有效地向前看。

The momentum term will make appropriate corrections and not overreach.

动量项将进行适当的更正，而不是超出范围。

In case future slope is steeper, momentum will speed up.
如果未来的坡度更陡，动量将加快。
In case future slope is low, momentum will slow down.
如果未来的坡度较低，动量将减慢。

阿达格勒 (Adagrad)

The motivation behind Adagrad is to have different learning rates for each neuron of each hidden layer for each iteration.

Adagrad背后的动机是， 对于每次迭代，每个隐藏层的每个神经元都有不同的学习率 。

But why do we need different learning rates?

但是为什么我们需要不同的学习率？

Data sets have two types of features:

数据集具有两种类型的功能：

Dense features, e.g. House Price Data set (Large number of non-zero valued features), where we should perform smaller updates on such features; and
密集特征，例如房屋价格数据集(大量非零值特征)，我们应该在其中进行较小的更新；和
Sparse Features, e.g. Bag of words (Large number of zero valued features), where we should perform larger updates on such features.
稀疏特征 ，例如单词袋(大量零值特征)，我们应该在其中进行较大的更新。

It has been found that Adagrad greatly improved the robustness of SGD, and is used for training large-scale neural nets at Google.

已经发现，Adagrad大大提高了SGD的鲁棒性，并在Google上用于训练大规模神经网络。

η : initial Learning rate
η：初始学习率
ϵ : smoothing term that avoids division by zero
ϵ：避免被零除的平滑项
w: Weight of parameters
w：参数权重

As the number of iterations increases, α increases. As α increases, learning rate at each time step decreases.

随着迭代次数的增加，α增加。随着α的增加，每个时间步的学习率都会降低。

One of Adagrad’s main benefits is that it eliminates the need to manually tune the learning rate. Most implementations use a default value of 0.01 and leave it at that.

Adagrad的主要好处之一是，它无需手动调整学习速度。大多数实现使用默认值0.01并保留该默认值。

Adagrad’s weakness is its accumulation of the squared gradients in the denominator. Since every added term is positive, the accumulated sum keeps growing during training. This in turn causes the learning rate to shrink and eventually become infinitesimally small, at which point the algorithm is no longer able to acquire additional knowledge. The next optimization algorithms aim to resolve this flaw.

阿达格勒(Adagrad)的弱点是它在分母中积累了平方梯度。由于每个增加的项都是正数，因此在训练期间累积的总和会不断增长。反过来，这导致学习率下降，并最终变得无限小，这时算法不再能够获取其他知识。下一个优化算法旨在解决这一缺陷。

Adadelta / RMSProp (Adadelta/RMSProp)

Adadelta/RMSProp are very similar in their implementation and they overcome the shortcomings of Adagrad’s accumulated gradient by using exponentially weighted moving average gradients.

Adadelta / RMSProp在实现上非常相似，它们通过使用指数加权移动平均梯度来克服Adagrad累积梯度的缺点。

Instead of inefficiently storing all previous squared gradients, we recursively define a decaying average of all past squared gradients. The running average at each time step then depends (as a fraction γ , similarly to the Momentum term) only on the previous average and the current gradient.

代替无效地存储所有先前的平方梯度，我们递归地定义所有过去平方梯度的衰减平均值。然后，每个时间步长的移动平均值仅取决于先前的平均值和当前梯度(类似于动量项，为分数γ)。

Any new input data points do not dramatically change the gradients, and will hence converge to the local minima with a smoother and shorter path.

任何新的输入数据点都不会显着改变梯度，因此将以更平滑，更短的路径收敛到局部最小值。

亚当 (Adam)

Adam optimizer is highly versatile, and works in a large number of scenarios. It takes the best of RMS-Prop and momentum, and combines them together.

Adam优化器具有高度的通用性，可以在多种情况下使用。它充分利用了RMS-Prop和动量，并将它们结合在一起。

Whereas momentum can be seen as a ball running down a slope, Adam behaves like a heavy ball with friction, which thus prefers flat minima in the error surface.

动量可以看成是一个顺着斜坡滑下的球，而亚当的举动就像是一个带有摩擦的沉重的球，因此，它更喜欢在误差表面上保持平坦的最小值。

As it can be anticipated, Adam accelerates and decelerates thanks to the component associated to momentum. At the same time, Adam keeps its learning rate adaptive which can be attributed to the component associated to RMS-Prop.

可以预见，由于动量相关的分量，亚当加速和减速。同时，Adam保持其学习率自适应，这可以归因于与RMS-Prop相关的组件。

Default values of 0.9 for β1 is 0.999 for β2 is , and 10pow(-8) for ϵ. Empirically, Adam works well in practice and compares favorably to other adaptive learning-method algorithms.

β1的默认值为0.9，β2的默认值为0.999，ϵ的默认值为10pow(-8)。根据经验，Adam在实践中表现良好，并且可以与其他自适应学习方法算法相比。