三个数差的平方公式推导过程_数学上有哪些巧妙的证明过程？

有关数学公式的证明很多，下面介绍几个常见公式的巧妙证明过程。

(1)自然数的立方和=自然数之和的平方

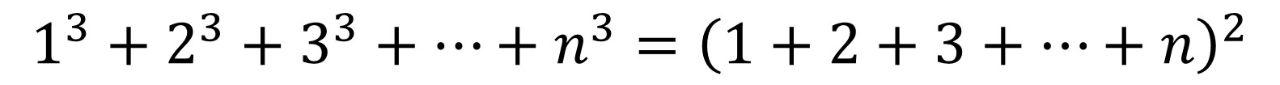
上述等式的左边为自然数的立方和，等式的右边为自然数之和的平方。虽然通过分别推导出左右两边的计算公式就能证明该等式，但通过如下的图形很直观地就能证明上式：

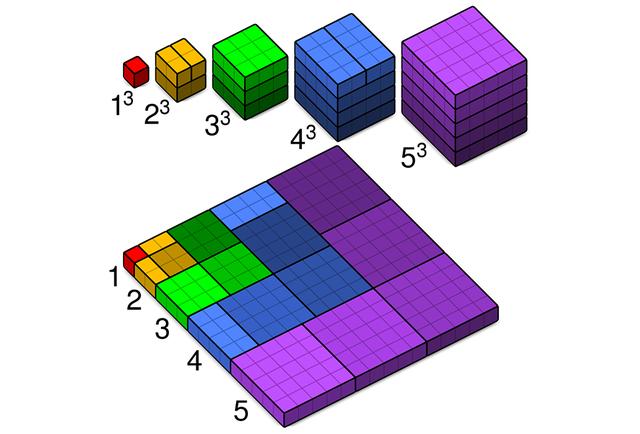
把自然数立方和的图形平铺看来，其中的正方体数量刚好是就是自然数之和的平方，所以就能证明上述等式成立。

(2)勾股定理

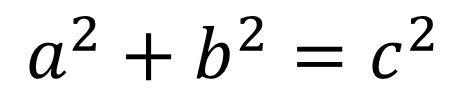
这个公式为勾股定理，我国在商朝时就已经发现了直角三角形的一个特例——勾三股四玄五，后来的中外数学家通过各种方法来证明这个公式。下面要介绍的是加菲尔德证法的变形方法，这可以很容易证明勾股定理：

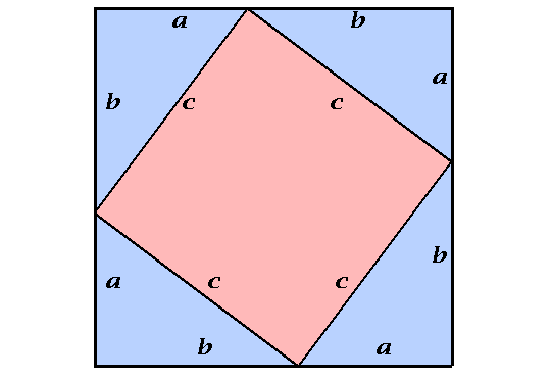
大正方形的面积为：

(a+b)^2

大正方形的面积也等于四个三角形的面积以及小正方形的面积之和：

4×(1/2ab)+c^2

由此可得下式：

(a+b)^2=4×(1/2ab)+c^2

化简之后，即可得勾股定理：

a^2+b^2=c^2

(3)欧拉恒等式

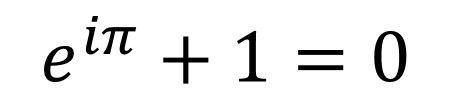
这个公式就是著名的欧拉恒等式，它被誉为最美的数学公式。一个十分简单的公式就结合了数学中最重要的常数——自然常数e、虚数单位i、圆周率π、自然数1、自然数0，以及最重要的数学符号——加号+、等号=。

欧拉恒等式源自于如下的欧拉公式：

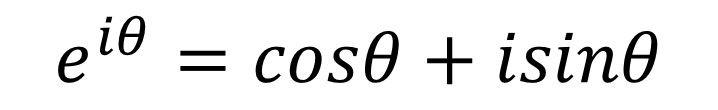
对欧拉公式的左边e^(iθ)进行泰勒展开可得：

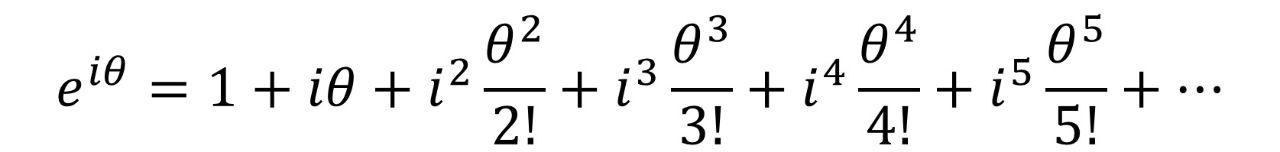
再分别对cosθ和sinθ进行泰勒展开可得：

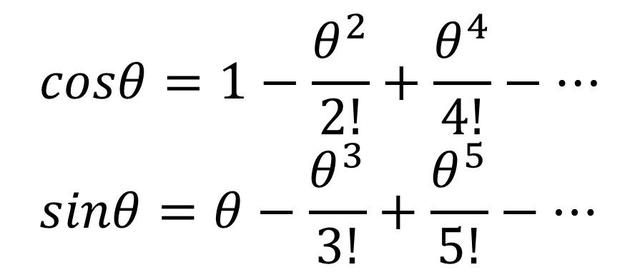
显然，cosθ与sinθ之和刚好等于e^(iθ)，由此就能证明欧拉公式成立。再令欧拉公式中的θ=π，即可得下式：

e^(iπ)=-1+0

对上式进行移项，最终就可以推导出欧拉恒等式的常见形式。

(4)证明圆周率是无理数

虽然人类早在三千多年前就已使用圆周率，但直到两百多年前，数学家才首次证明圆周率是一个无理数。圆周率是无理数的证明方法不少，下面要介绍的是数学家Ivan M. Niven给出的反证法，这种方法简单而又巧妙。

倘若π为有理数，必然存在整数a和b，使得下式成立：

π=a/b

构造如下两个函数：

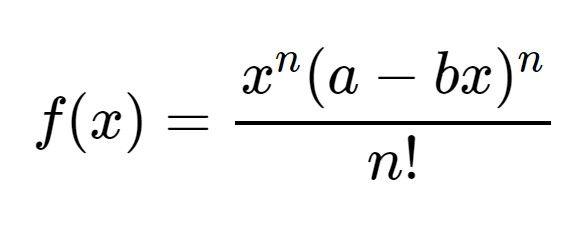
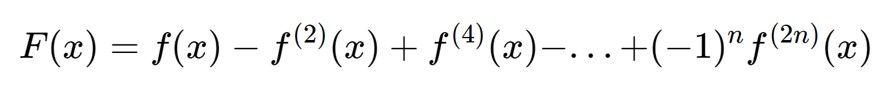
其中n为正整数。

显然，f^k(0)、f^k(π)、F(0)以及F(π)都为整数。而且f(x)和f^k(x)都会满足f(x)=f(π-x)，它们都在x=0以及x=π处可积。

再构造函数G(x)=F'(x)sinx-F(x)cosx，并对其进行求导可得：

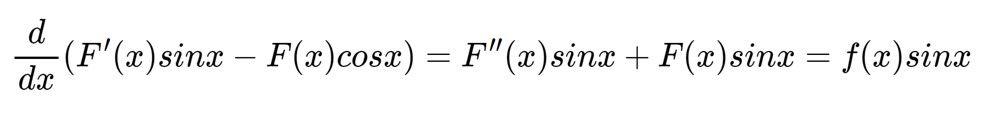
对上式两边从0到π都进行积分可得下式：

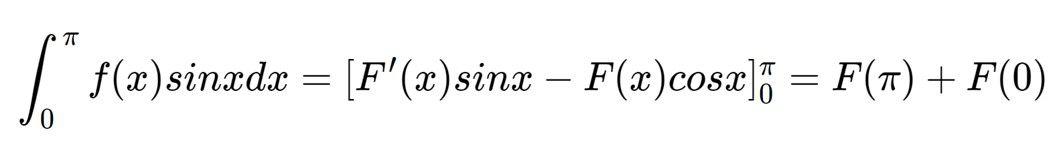
因为F(0)以及F(π)都为整数，故F(π)+F(0)亦是整数。当x∈(0, π)时，显然有f(x)>0且sinx>0，故f(x)sinx>0，所以F(π)+F(0)>0，并且f(x)sinx在[0, π]上的积分为正整数。

当x∈(0, π)时，显然有a-bx

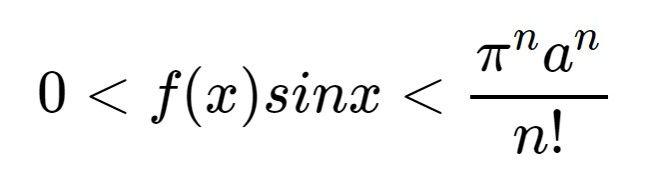
显然，当n→+∞时，f(x)sinx→0，由夹逼定理可得，f(x)sinx在[0, π]上的积分也会趋于0。然而，上述的推导表明这个积分是正整数，所以两者出现了矛盾。这意味着π=a/b不成立，所以圆周率必然为一个无理数。