四边形内接于圆定理_中考数学提分36计之第19计思维模型助你轻松搞定圆问题,提分必备...

A.思维模型综述

圆是初中数学知识的大综合,不论是代数还是几何,所有的知识几乎都能在圆中体现.新课标以来圆的部分内容在中考中的地位有所下降,题目难度有所降低,但是圆的命题还是中考的热点考题,在不少地区难度依然很大.

只要掌握以下七个思维模型,圆的问题就有规律可找了.

(1)遇到有关弦的问题时,通常要作出垂直于弦的半径,利用垂径定理求有关的量;还常常连接弦的两个端点和圆心,构造等腰三角形.

(2)遇到直径时,常常添加直径所对的圆周角,得到直角三角形.

(3)遇到90°的圆周角时,常连接圆周角的两边与圆的交点,得到直径.

(4)遇到切线时,添加过切点的半径,得到垂直,即一切就垂.

(5)遇到要证明切线时,若有交点,则连半径,证垂直;若无交点,则作垂直,证半径.

(6)遇到三角形的内切圆时,连接内心与三角形各顶点,利用内心的性质.

(7)遇到三角形的外接圆时,连接外心和三角形各顶点,利用外心的性质.

B．最新考题精析

1．(2019•中原区校级模拟)已知圆O的半径为5，P为圆O内一点，且OP＝3，则过点P的所有弦中，弦长是整数的共有( )

A．4条B．3条C．2条D．1条

【解析】先求出过P点的弦长的取值范围，然后判断出弦长为整数的弦有几条．如图，过P作弦AB⊥OP，交⊙O于A、B，连接OA，

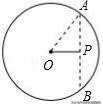
Rt△OAP中，OP＝3，OA＝5，根据勾股定理，得AP＝4，即由垂径定理得：AB＝2AP＝8，故过点P的弦的长度都在8～10之间，因此弦长为8、9、10，当弦长为8、10时，过P点的弦分别为弦AB和过P点的直径，分别有一条；当弦长为9时，根据圆的对称性知，符合条件的弦应该有两条；故弦长为整数的弦共有4条，故选：A．

2．(2019•定安县一模)如图，⊙A过点O(0，0)，C(2√3，0)，D(0，2)，点B是x轴下方⊙A上的一点，连接BO，BD，则∠OBD的度数是( )

A．15°B．30°C．45°D．60°

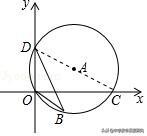
【解析】连接DC，在Rt△DOC中，tan∠OCD＝OD/OC=2/2√3=√3/3，

则∠OCD＝30°，由圆周角定理得，∠OBD＝∠OCD＝30°，故选：B．

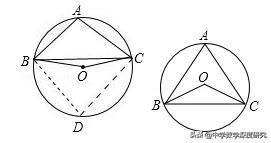
3．(2018秋•滨湖区期末)若等腰△ABC内接于⊙O，AB＝AC，∠BOC＝100°，则△ABC底角的度数为( )

A．65°B．25°C．65°或 25°D．65°或 30°

【解析】画出相应图形，分△ABC为锐角三角形和钝角三角形2种情况解答即可．(1)圆心O在△ABC外部，在优弧BC上任选一点D，连接BD，CD．

∴∠BDC＝1/2∠BOC＝50°，∴∠BAC＝180°﹣∠BDC＝130°；

∵AB＝AC，∴∠ABC＝(180°﹣∠BAC)÷2＝25°；

(2)圆心O在△ABC内部．∠BAC＝1/2∠BOC＝50°，

∵AB＝AC，∴∠ABC＝(180°﹣∠BAC)÷2＝65°．

综上所述，△ABC底角的度数为65°或 25°，故选：C．

4．(2019•鄞州区一模)如图，AB是半圆O的直径，点C在半圆上(不与A，B重合)，DE⊥AB于点D，交BC于点F，下列条件中能判别CE是切线的是( )

A．∠E＝∠CFEB．∠E＝∠ECFC．∠ECF＝∠EFCD．∠ECF＝60°

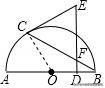
【解析】连接OC，∵OC＝OB，∴∠OCB＝∠B，

∵DE⊥AB，∴∠BDF＝90°，∴∠B+∠DFB＝90°，

∵∠EFC＝∠BFD，∴∠B+∠EFC＝90°，

∵∠ECF＝∠EFC，∴∠OCB+∠ECF＝90°，∴CE是⊙O的切线．故选：B．

5．(2019•宁波模拟)如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，G是弧AC上的任意一点，AG，DC的延长线相交于点F．

(1)若CD＝8，BE＝2，求⊙O的半径；

(2)求证：∠FGC＝∠AGD；

(3)若直径AB＝10，tan∠BAC＝1/2，弧AG＝弧BG，求DG的长．

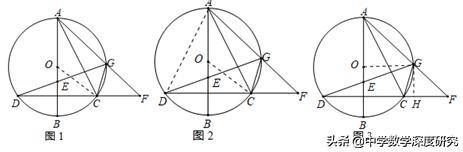
【解答】(1)解：连接OC．如图1所示：

设⊙O的半径为R．∵CD⊥AB，∴DE＝EC＝4，

在Rt△OEC中，∵OC²＝OE²+EC²，

∴R²＝(R﹣2)²+4²，解得：R＝5，即⊙O的半径为5；

(2)证明：连接AD，如图2所示：

∵弦CD⊥AB,∴弧AD=弧AC，∴∠ADC＝∠AGD，

∵四边形ADCG是圆内接四边形，

∴∠ADC＝∠FGC，∴∠FGC＝∠AGD；

(3)解：如图2中，连接OG，作GH⊥DF于H．

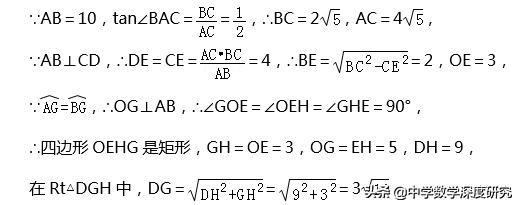
6．(2019•贵阳模拟)如图①，将一块含30°角的三角板和一个量角器拼在一起，如图②是拼接示意图，三角板斜边AB与量角器所在圆的直径MN重合且∠CAB＝30°，其量角器最外缘的读数是从N点开始(即N点的读数为0)，现有射线CP绕点C从CA的位置开始按顺时针方向以每秒2度的速度旋转到CB位置，在旋转过程中，射线CP与量角器的半圆弧交于点E．

(1)当旋转7.5秒时，连结BE，E点处量角器上的读数为_____ 度；

(2)在(1)的条件下求证BE＝CE；

(3)设旋转x秒后，E点处量角器上的读数为y度，写出y与x的函数表达式．

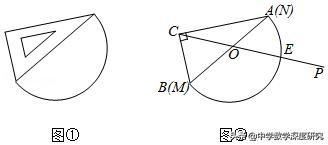
【解答】由于∠ACB＝90°，AB为斜边，所以此量角器所在圆是以AB中点O为圆心，AB为直径的圆．连接OE、BE，∠ACE＝7.5×2＝15°，

∵∠ACE和∠ABE都是弧AE所对的圆周角，∴∠ABE＝∠ACE＝15°．

∵OE＝OB，∴∠AOE＝2∠ABE＝30°，即E点处量角器上的度数为30度．

故答案为30；

(2)∠ECB＝90°﹣15°＝75°，∠EBC＝90°﹣30°+15°＝75°，

∴∠ECB＝∠EBC．∴BE＝CE；

(3)当旋转x秒后，∠ACE＝2x°，根据圆周角性质可知∠ABE＝∠ACE＝2x°，

∵OB＝OE，∴∠AOE＝2∠ABE＝4x°．即y＝4x．

7．(2019•河南模拟)如图，在△ABC中，AB＝8，∠CBA＝30°，以AB为直径作半圆O，半圆O恰好经过点C，点D在线段AB上运动，点E与点D关于AC对称，DF⊥DE于点D，并交EC的延长线于点F．

(1)求证：CE＝CF

(2)填空：①若DF与半圆O相交于点P，则当点D与点O重合时，弧BF的长为____

②在点D的运动过程中，当EF与半圆O相切时，EF的长为 ．

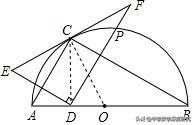
【解答】(1)连接CD，如图1所示，

∵点E与点D关于AC对称，∴CE＝CD，∴∠E＝∠CDE，

∵DF⊥DE，∴∠EDF＝90°，∴∠E+∠F＝90°，∠CDE+∠CDF＝90°，

∴∠F＝∠CDF，∴CD＝CF，∴CE＝CD＝CF；

(2)①∵点E与点D关于AC对称，∴DE⊥AC，

∵∠ACB＝∠EDF＝90°，∴DF⊥BC，∴∠FDB＝60°，

②连接OC，CD，∵∠CBA＝30°，∴∠AOC＝60°，

∵OC＝OA，∴△AOC是等边三角形，

∵EF与半圆O相切，∴∠ACE＝∠B＝30°，∴∠ACD＝30°，∴∠ADC＝90°，

∴∠OCD＝30°，∴CD＝sin60°•AC＝2√3，

∵CE＝CD＝CF，∴EF＝2CD＝4√3．故答案为：4√3．

C.深入归纳总结(歌诀)

圆的证明不算难，常把半径直径连；

有弦可作弦心距，它定垂直平分弦；

直径是圆最大弦，直圆周角立上边，

它若垂直平分弦，垂径、射影响耳边；

还有与圆有关角，勿忘相互有关联，

圆周、圆心、弦切角，细找关系把线连。

同弧圆周角相等，证题用它最多见，

圆中若有弦切角，夹弧找到就好办；

圆有内接四边形，对角互补记心间，

外角等于内对角，四边形定内接圆；

直角相对或共弦，试试加个辅助圆；

若是证题打转转，四点共圆可解难；

要想证明圆切线，垂直半径过外端，

直线与圆有共点，证垂直来半径连，

直线与圆未给点，需证半径作垂线；

四边形有内切圆，对边和等是条件；

D．最新考题精炼

需要详细答案的word版本，可留下信箱，抽时间可发送与你，期待你的关注，留言互动。