向量遍历_矩阵和向量的故事（20）

上节最后提到这一篇开始观察一个具体的线性变换

,这个线性变换是

为了观察这个线性变换

的具体作用, 可以从图形入手，视觉是最直观的，所以我们选择一个常见的图形，比如说圆，比如矩形，当然也可以选择一个不常见的图形，比如任何一个不规则的多边形。选择这些有边界的图形是因为这些有边界的形状给人的视觉有很强的冲击感，就是说把这些边界涂黑以后，这个图形内的点和图形外的点在直觉上区分会十分容易。

我们可以随便选择一个这样有边界的图形去观察，这里就选正方形，为了方便，我们把正方形单位化，选择一个边长是1的正方形。

然后，在线性变换

处理的向量空间

里面，用向量的语言去说明这个单位正方形，这个时候可以建立一个坐标系，现在把这个正方形左下角对应原点，左下角关联的两边对应这坐标轴的横轴

,纵轴

。这样的处理就把这个正方形处于在这个向量空间

中，然后我们寻求一些解析的表达。

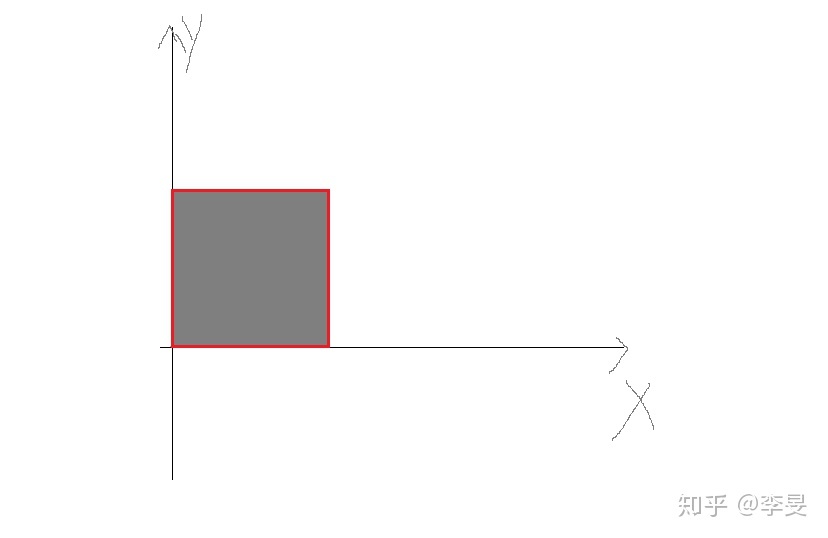
如下图这样：

单位正方形就是红色边界围起来里面的所有的点，这个是我们对于这个单位正方形在这个向量空间里面的形象描述。

现在

是这个坐标系的标准基底，对于这个单位正方形里面的任何一个点P,那么假设表示点P的向量是

;

那么

作为这个正方形的解析表达式是可以成立的。

就是说一个二元组

在

这个限制条件下可以代表这个正方形内的一个点；

遍历完这组限制条件，就完成了对于这个正方形的刻画。

接着为了观察线性变换

，把

施加在这个正方形上每一个点，然后观察每一个点被处理后变得怎么样，然后整个正方形在宏观上最终会变得怎么样？

比如对于右下角的点

，右上角的点

用

进行处理：

点

代表的向量是

那么

这样用处理后的向量

, 对应对应于点

;

同样的处置过程：

点

变成了点

如果是任何一个点

，

对应于点

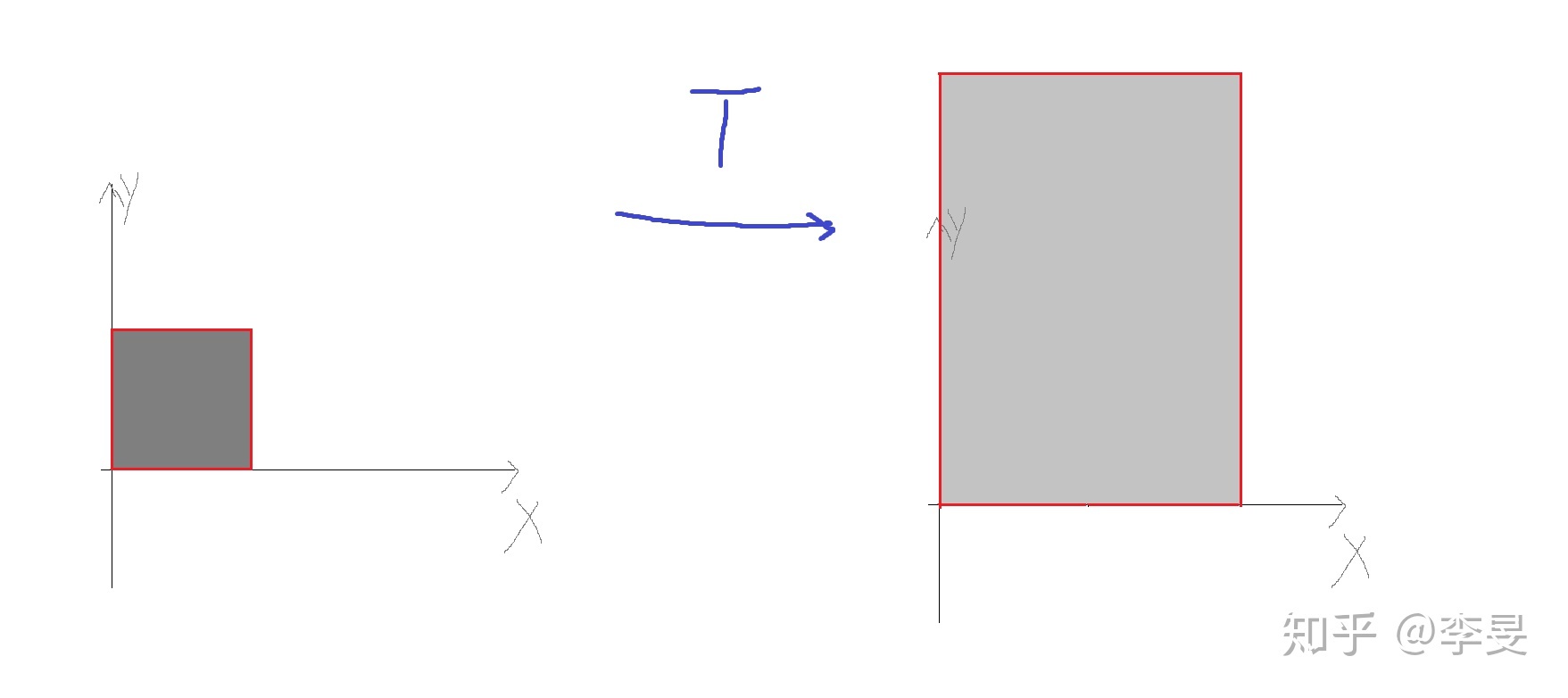
每个点坐标在横向分别像是被拉长2倍，纵向上被拉长3倍，所以这个单位正方形，变成了一个长方形。

如下图：

线性变换

就像是拉长了斜着一定角度拉长正方形；

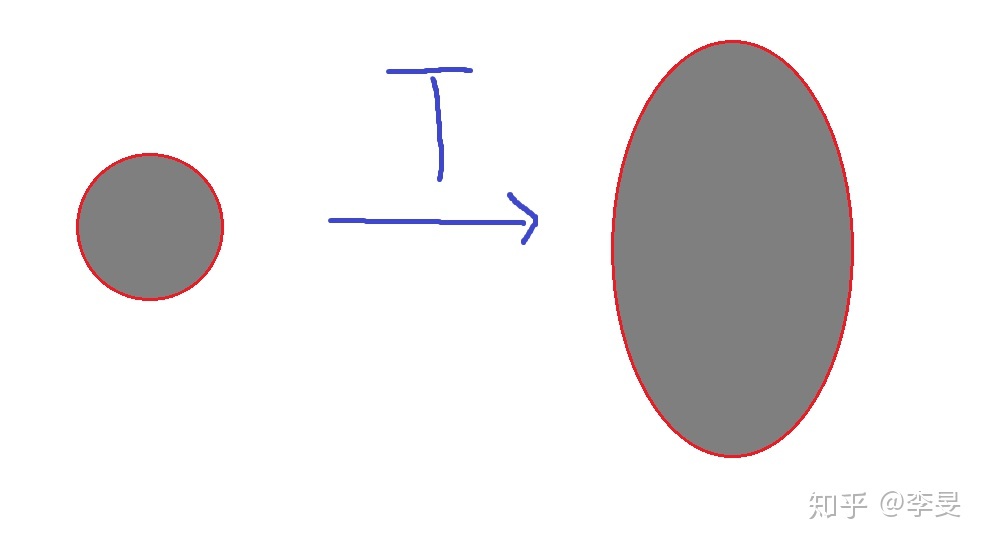
如果这个形状换成了圆形，我们可以想象一下，会发生这样的变换：

到这里我们知道了线性变换

的形象作用；

产生这样作用的

就具有这样的表达式：

现在可以找一下矩阵的形式：

首先正方形的任意一个点P对应的向量是

,用

处理后是

,如果全部用向量的语言就有：

向量

对应的两个列矩阵

,

那么向量

对应的矩阵

是

向量

对应的矩阵

这个矩阵写开来就是：

所以

现在我们找到了两个矩阵，向量

对应的矩阵

,向量

对应的矩阵

它们的形式分别是：

对照一下这两个矩阵线性变换

的作用就像是在中间插入了一个这样的矩阵

，这样的矩阵被称为转换矩阵；

当从矩阵形式上来说，一个线性变换

的作用就是在基底的矩阵表示和坐标的矩阵表示之间插入了一个新的转换矩阵

;

从这个角度上来看，用矩阵去算是很便捷的，只要找到转换矩阵，把这个矩阵执行一个插入操作，其他的运算就按照矩阵定义的规则下去算，那么就可以完成一个整个线性变换

,这样不需要图形的直观，只要严格按照这样的规则去算就行。对于转换矩阵是

很简单的线性变换来说，可能意义不是很大。但是如果这个转换矩阵很复杂，至少图形上超出了一些想象，但是我们知道线性这个过程依旧可以靠矩阵去算，那么这层对应，由线性变换到矩阵这层的对应就十分有价值。