正弦函数_理解三角函数诱导公式的原理，远比记住口诀更重要

1.单位圆中的三角函数定义

在上篇文章中，我们给出了单位圆中的三角函数定义。即在圆心在原点的单位圆中，任意角对应圆上一点(x, y)相应的三角函数定义为

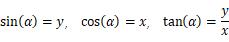
从任意角的三角函数定义中，我们了解到正弦、余弦和正切函数均为周期函数，因此，我们首先学习一个周期内的函数值就足够了。

2.同一个2π周期内的三角函数转化

现在我们从定义出发，观察三角函数在一个周期内的特征，能得到哪些结论呢？

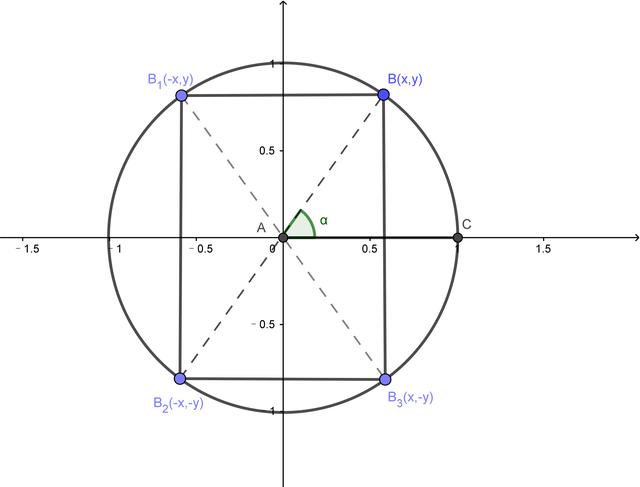
单位圆上任意一个点在每个象限都存在其对称的点(x轴对称、y轴对称、原点中心对称)，这些对称的点有个特点就是其横坐标的绝对值相同、纵坐标的绝对值也相同，如上图所示中的四个点。单位圆上每个点对应的角度，其正弦值为点坐标的y值、余弦值为点坐标的x值。

在那么四个象限互相对称的点处，其正弦值的绝对值相同、余弦值的绝对值也相同、正切值的绝对值当然也是相同的。这说明，四个象限的点对应的三角函数值都可以用第一象限对应的三角函数值表示，区别仅仅是正负号可能会有差异！

第二象限与第一象限对应关系：x异号、y同号，即

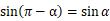
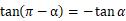
第三象限与第一象限对应关系：x异号、y异号，即

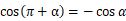
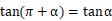
第四象限与第一象限对应关系：x同号、y异号，即

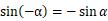
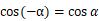
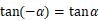
3.正弦函数和余弦函数的关系

然后我们再来看正弦函数和余弦函数有什么关系。

首先，坐标轴x和坐标轴y是什么关系呢？从旋转的角度来说，可以将y轴看作是x轴沿着原点逆时针旋转π/2得来的。若以y轴为角的起始位置，那么角α对应的余弦值为y，正弦值为-x；若以x轴为角的起始位置，它应该是角α+π/2处，其正弦值为y和余弦值为x。即在同一个点，在两种定义下得到的三角函数值有下列关系。

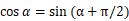
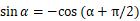
这便是正弦函数和余弦函数之间的关系。

4.诱导公式及其原理

综合上述结论，任意角的三角函数都可转化为锐角三角函数，正弦函数和余弦函数也可互相转化，这就是三角函数一系列诱导公式的原理！

对于正余弦三角函数，有个诱导公式口诀为：“奇变偶不变，符号看象限”。

前半句的意思解释为，角度±α加上π/2的奇数倍时，则正弦函数转化为α的余弦函数、余弦函数转化为α的正弦函数，即

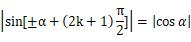
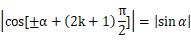
角度±α加上π/2的偶数倍(即π的整数倍)时，正弦函数还是转化为α的正弦函数、余弦函数还是转化为α的余弦函数，即

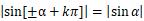
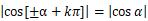
后半句意思解释为，上述几个等式绝对值展开后，假定α为锐角时，首先确定等式左边三角函数括号中表达式对应的角处于哪个象限，然后根据正弦或是余弦确定此象限对应的纵坐标或横坐标的正负号，即对应等式右边去除绝对值后的正负号。

本文由小朱与数学原创，欢迎关注，带你一起长知识！