简介:本资料包旨在帮助ACM竞赛参与者深入理解并应用数据结构。通过C语言的讲解,涵盖数组、链表、栈、队列、树、图、哈希表和堆等数据结构的原理及其实现。每个数据结构都包含C语言的代码实例,帮助学习者理解其工作原理并熟练掌握相关算法。掌握这些内容不仅能够提升编程技能,还有助于在ACM及其他编程挑战中取得成功。 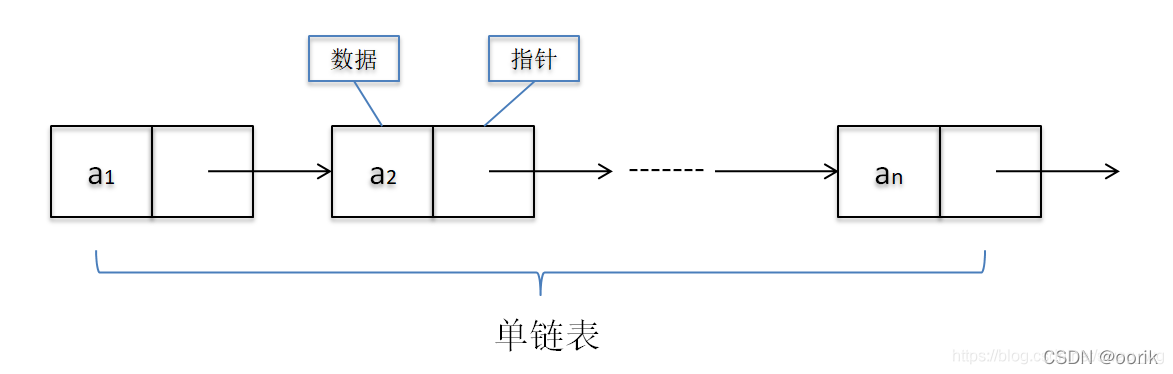
1. 数据结构在ACM竞赛中的重要性
在ACM国际大学生程序设计竞赛(ACM-ICPC)中,数据结构扮演着至关重要的角色。竞赛题目往往要求选手在有限的时间内解决问题,而选择恰当的数据结构可以极大地提高算法的效率,从而节省宝贵的时间。一个精心设计的数据结构可以使代码更加简洁、高效,并且能够更好地管理复杂的数据关系和操作。例如,对于需要快速检索或插入的数据,数组可能不是最佳选择,而哈希表或平衡二叉搜索树则能提供更优的性能。在解决诸如最短路径、图的连通性、序列匹配等问题时,合适的数据结构可以转换为关键的优化步骤。本章将探索数据结构在ACM竞赛中的作用,并简要介绍一些基本的数据结构以及它们在竞赛中的应用。
2. C语言特性及其在数据结构学习中的作用
2.1 C语言的基本语法和数据类型
2.1.1 变量的声明与定义
在C语言中,变量是数据存储的基本单位。声明变量时,必须指定数据类型,它决定了变量可以存储的数据类型以及占用的内存大小。C语言的变量声明语法如下:
type variable_name;
其中 type 是数据类型(如 int , float , double , char 等), variable_name 是变量名。例如:
int number;
float pi;
char letter;
在声明之后,可以在同一语句中对变量进行定义,并初始化:
int number = 0;
float pi = 3.14;
char letter = 'a';
2.1.2 基本数据类型及其操作
C语言提供了多种基本数据类型,它们是最基本的数据单位,每种类型的数据占用内存大小是固定的,但这个大小可以因不同的系统架构(如32位和64位系统)而有所不同。
- 整型(int):用于存储整数。
- 浮点型(float, double):用于存储小数。
- 字符型(char):用于存储单个字符。
- 枚举型(enum):用于表示一组命名常数。
这些类型之间的操作涉及算术运算( + , - , * , / ),关系运算( == , != , > , < , >= , <= ),逻辑运算( && , || , ! )等,以及位运算( & , | , ^ , << , >> )。
2.2 C语言的控制结构与指针使用
2.2.1 条件语句与循环语句
C语言提供了多种控制结构来控制程序的流程。最常用的控制结构包括条件语句(if, switch)和循环语句(while, do-while, for)。
条件语句允许根据不同的条件执行不同的代码块:
if (condition) {
// 条件为真时执行的代码
} else {
// 条件为假时执行的代码
}
循环语句用于重复执行同一代码块,直到满足特定条件:
while (condition) {
// 条件为真时重复执行的代码
}
2.2.2 指针的概念及其在数据结构中的应用
指针是C语言的核心特性之一,它存储了变量的内存地址,允许直接访问内存中的数据。指针的操作包括指针的声明、初始化、解引用和指针算术等。
- 指针的声明:
type *pointer_name; - 指针的初始化:
pointer_name = &variable; - 解引用指针:
*pointer_name - 指针算术:
pointer_name + 1(移动到下一个存储相同类型数据的位置)
指针在数据结构中的应用非常广泛,如实现链表、树等动态数据结构。下面是一个简单的单链表节点的定义和创建的例子:
typedef struct Node {
int data;
struct Node *next;
} Node;
Node* createNode(int data) {
Node *newNode = (Node*)malloc(sizeof(Node));
if (newNode == NULL) {
exit(1); // 内存分配失败时退出
}
newNode->data = data;
newNode->next = NULL;
return newNode;
}
2.3 C语言的内存管理和动态分配
2.3.1 内存分配与释放的基本原理
在C语言中,程序员需要手动管理内存。 malloc() , calloc() , realloc() 和 free() 是管理堆内存的关键函数。
-
malloc():分配指定大小的内存。 -
calloc():分配并初始化内存。 -
realloc():重新分配内存大小。 -
free():释放已分配的内存。
例如,动态分配一个整数数组:
int *array = (int*)malloc(n * sizeof(int));
if (array == NULL) {
exit(1); // 内存分配失败时退出
}
使用完毕后,应当释放这块内存:
free(array);
2.3.2 动态数组和链表的内存操作实践
动态数组和链表是两种在C语言中常见的动态数据结构。动态数组是通过连续内存空间存储元素,而链表则是通过节点指针连接。
例如,创建和使用动态数组:
int *dynArray = (int*)malloc(n * sizeof(int));
for (int i = 0; i < n; ++i) {
dynArray[i] = i;
}
free(dynArray);
链表的内存操作则涉及到指针的分配和释放,如前面提到的节点创建示例。
在ACM竞赛中,灵活运用指针和动态内存管理可以帮助参赛者高效地实现复杂的数据结构,从而解决各种算法问题。对于长期从事IT行业的专业人士来说,深入理解这些概念不仅是对基础知识的巩固,也是对优化程序性能和处理内存泄漏等潜在问题的重要一步。
3. 数组、链表、栈、队列、树、图、哈希表和堆的基本概念及实现
3.1 线性结构的基本概念及实现
线性结构是指元素之间存在一对一关系的线性序列。本节将详细介绍两种基本的线性结构——数组和链表,以及它们在实现栈和队列时的不同应用场景。
3.1.1 数组与链表的定义及其应用场景
数组(Array)是具有相同类型数据元素的有序集合,数据在内存中连续存储。数组允许快速地随机访问元素,但插入和删除操作较为低效,尤其是当需要在数组中间插入或删除元素时,因为这涉及到移动大量元素。
链表(LinkedList)是由一系列节点组成的线性集合,每个节点包含数据域和指针域,指针指向下一个节点。链表的插入和删除操作高效,因为它们只涉及到指针的修改,但随机访问元素的效率较低。
数组与链表的选择依赖于具体的应用场景。数组适用于元素数量固定不变或按索引频繁访问的情况;链表适用于元素频繁插入和删除的场景。
// 简单的单链表节点定义
struct Node {
int data;
struct Node* next;
};
3.1.2 栈与队列的基本操作和性质
栈(Stack)是一种后进先出(LIFO)的数据结构,支持两种操作:push(压栈)和pop(弹栈)。栈的经典应用场景包括函数调用的实现、撤销操作的历史记录等。
队列(Queue)是一种先进先出(FIFO)的数据结构,支持两种操作:enqueue(入队)和dequeue(出队)。队列用于任务调度、缓冲处理等场景。
// 栈的简单实现
#define MAXSIZE 100 // 定义栈的最大容量
int stack[MAXSIZE]; // 栈数组
int top = -1; // 栈顶指针
void push(int value) {
if (top < MAXSIZE - 1) {
top++;
stack[top] = value;
} else {
printf("Stack overflow\n");
}
}
int pop() {
if (top >= 0) {
int value = stack[top];
top--;
return value;
} else {
printf("Stack underflow\n");
return -1;
}
}
3.2 非线性结构的基本概念及实现
3.2.1 二叉树的遍历和操作
二叉树(Binary Tree)是一种特殊的树形数据结构,其中每个节点最多有两个子节点,分别是左子节点和右子节点。二叉树在查找、排序、遍历等领域有着广泛的应用。
二叉树的遍历方式主要有三种:前序遍历、中序遍历和后序遍历。前序遍历先访问根节点,然后遍历左子树,最后遍历右子树。中序遍历是先遍历左子树,然后访问根节点,最后遍历右子树。后序遍历先遍历左子树和右子树,最后访问根节点。
// 二叉树节点的定义
struct TreeNode {
int value;
struct TreeNode* left;
struct TreeNode* right;
};
// 二叉树的前序遍历
void preorderTraversal(struct TreeNode* root) {
if (root == NULL) return;
printf("%d ", root->value); // 访问根节点
preorderTraversal(root->left); // 遍历左子树
preorderTraversal(root->right); // 遍历右子树
}
3.2.2 图的表示和搜索算法
图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成。图的表示方法主要有两种:邻接矩阵和邻接表。邻接矩阵适用于顶点数量较少的稠密图,邻接表适用于顶点数量较多的稀疏图。
图的搜索算法包括深度优先搜索(DFS)和广度优先搜索(BFS)。DFS通过递归方式遍历图中的每个节点,而BFS则通过队列实现对节点的逐层遍历。
// 图的邻接表表示
#define MAX_VERTICES 100 // 图的最大顶点数
struct AdjList {
struct TreeNode* head; // 指向链表头节点的指针
};
struct Graph {
struct AdjList adjList[MAX_VERTICES]; // 邻接表数组
int nVertices; // 图中顶点的数量
};
// 深度优先搜索的简单实现
void DFS(struct Graph* graph, int vertex, int visited[]) {
// 访问当前顶点
visited[vertex] = 1;
printf("Visited %d\n", vertex);
// 遍历所有邻接顶点
struct AdjList* list = &graph->adjList[vertex];
struct TreeNode* node = list->head;
while (node != NULL) {
if (visited[node->value] == 0) {
DFS(graph, node->value, visited);
}
node = node->next;
}
}
3.3 高级数据结构的基本概念及实现
3.3.1 哈希表的设计原理及冲突解决
哈希表(Hash Table)是一种通过哈希函数将键(Key)映射到存储桶(Bucket)的数据结构,它允许快速的插入、删除和访问操作。哈希表的关键在于哈希函数的设计和冲突解决策略。
常见的冲突解决方法有开放定址法和链地址法。在开放定址法中,当冲突发生时,会顺序检查下一个存储桶,直到找到一个空桶为止。在链地址法中,每个存储桶是链表的头节点,冲突元素以链表形式存储。
// 哈希表的简单实现
#define TABLE_SIZE 100 // 哈希表大小
int hashTable[TABLE_SIZE]; // 哈希表数组
int hashFunction(int key) {
return key % TABLE_SIZE; // 简单的哈希函数
}
void insert(int key) {
int index = hashFunction(key);
hashTable[index] = key; // 存储键值
}
int search(int key) {
int index = hashFunction(key);
if (hashTable[index] == key) {
return index; // 找到键值
}
// 冲突解决:线性探测直到找到空桶或者匹配的键值
int originalIndex = index;
do {
index = (index + 1) % TABLE_SIZE;
if (hashTable[index] == key) {
return index;
}
} while (hashTable[index] != 0 && index != originalIndex);
return -1; // 未找到键值
}
3.3.2 堆的性质与优先队列的实现
堆(Heap)是一种特殊的完全二叉树,满足每个节点的值都大于或等于其子节点的值,这样的堆称为最大堆。堆可以高效地实现优先队列(Priority Queue),优先队列允许插入新元素,以及删除最大元素(在最大堆中)或最小元素(在最小堆中)。
堆的基本操作包括:插入元素(sift up)、删除堆顶元素(sift down)、建堆(heapify)。堆的插入和删除操作的时间复杂度均为O(log n),其中n是堆中元素的数量。
// 堆的简单实现(最大堆)
int heap[MAX_VERTICES]; // 堆数组
int heapSize; // 堆中元素的数量
void siftUp(int index) {
while (index > 0 && heap[(index - 1) / 2] < heap[index]) {
int temp = heap[(index - 1) / 2];
heap[(index - 1) / 2] = heap[index];
heap[index] = temp;
index = (index - 1) / 2;
}
}
void insertHeap(int value) {
heapSize++;
heap[heapSize - 1] = value;
siftUp(heapSize - 1);
}
void siftDown(int index) {
int largest = index;
int left = 2 * index + 1;
int right = 2 * index + 2;
if (left < heapSize && heap[left] > heap[largest]) {
largest = left;
}
if (right < heapSize && heap[right] > heap[largest]) {
largest = right;
}
if (largest != index) {
int temp = heap[index];
heap[index] = heap[largest];
heap[largest] = temp;
siftDown(largest);
}
}
void deleteHeap() {
if (heapSize > 0) {
int rootValue = heap[0];
heap[0] = heap[heapSize - 1];
heapSize--;
siftDown(0);
return rootValue;
}
}
在本章节中,我们详细介绍了数组、链表、栈、队列、二叉树、图、哈希表和堆的基本概念及实现。每一节都包含了具体的数据结构定义、操作和应用场景,旨在为读者提供一个关于线性结构和非线性结构在ACM竞赛中应用的全面概述。理解这些基本概念和实现方式,对于在算法竞赛中快速准确地解决问题至关重要。
4. 数据结构的内在工作原理及C语言实现
4.1 数据结构的算法复杂度分析
在数据结构的学习与应用中,算法复杂度分析是不可或缺的一环,它帮助我们理解算法的时间和空间效率,从而选择最合适的算法解决特定问题。
4.1.1 时间复杂度与空间复杂度的定义和计算
时间复杂度描述了算法运行时间随着输入数据规模增长的变化趋势,通常表示为最坏情况下的渐进时间复杂度。常见的符号包括O(1)、O(log n)、O(n)、O(n log n)、O(n^2)等。对于简单算法,我们可以通过直接计算操作次数来估算时间复杂度,但对于更复杂的算法,通常需要通过递归树或主定理来分析。
空间复杂度是衡量算法在运行过程中临时占用存储空间大小的一个量度。它同样关注最坏情况下的空间需求,但需要注意的是,空间复杂度不仅包括输入数据所占用的空间,还包括算法执行过程中产生的额外空间,例如递归调用栈或动态分配的内存等。
4.1.2 算法优化的策略和方法
为了优化算法,减少时间或空间复杂度,可以采取以下策略: - 减少不必要的计算,比如通过备忘录技术存储已经计算过的结果。 - 采用更高效的算法来替代原有的低效算法。 - 优化数据结构设计,如使用哈希表来替代线性查找等。 - 分而治之,将大问题分解为小问题,分别解决后再合并结果。 - 利用算法的特性进行优化,比如在排序算法中使用稳定的排序而非不稳定的排序来保持相同值的顺序等。
4.2 C语言实现数据结构的高级技巧
C语言提供了丰富的特性,使得开发者可以使用低级内存操作来实现高效的复杂数据结构。
4.2.1 复杂数据结构的内存管理
内存管理是实现复杂数据结构时的核心问题之一。内存泄漏、指针错误和内存碎片等问题都可能影响程序的稳定性和性能。在C语言中,可以使用手动内存管理,如 malloc 、 calloc 、 realloc 和 free 来分配和释放内存。
以下是一个简单的动态数组实现的示例,它展示了如何手动管理内存:
#include <stdio.h>
#include <stdlib.h>
void resize_array(int **array, int *size, int new_size) {
int *new_array = realloc(*array, new_size * sizeof(int));
if (new_array == NULL) {
exit(EXIT_FAILURE); // 内存分配失败
}
*array = new_array;
*size = new_size;
}
int main() {
int size = 10;
int *array = malloc(size * sizeof(int));
for (int i = 0; i < size; ++i) {
array[i] = i;
}
resize_array(&array, &size, size * 2);
for (int i = size; i < size * 2; ++i) {
array[i] = i;
}
// 使用完毕后释放内存
free(array);
return 0;
}
在上述代码中,我们首先创建了一个大小为10的数组,然后使用 resize_array 函数将其大小加倍。此函数使用 realloc 来调整数组的大小,如果分配失败,则退出程序。
4.2.2 结构体联合和位操作在数据结构中的应用
结构体联合允许我们将不同类型的数据存储在相同的内存位置,这对于节省内存非常有用。位操作则允许开发者在单个字节或位级别上进行操作,非常适合实现紧凑的数据结构。
例如,可以使用结构体和位操作来实现一个简单的位图,它用于跟踪一定范围内的整数是否被设置:
#include <stdio.h>
#include <stdlib.h>
#define RANGE 1000 // 范围大小
void set_bit(unsigned char *bitmap, int bit) {
bitmap[bit / 8] |= (1 << (bit % 8));
}
void clear_bit(unsigned char *bitmap, int bit) {
bitmap[bit / 8] &= ~(1 << (bit % 8));
}
int is_bit_set(unsigned char *bitmap, int bit) {
return bitmap[bit / 8] & (1 << (bit % 8));
}
int main() {
unsigned char *bitmap = calloc(1, (RANGE + 7) / 8);
set_bit(bitmap, 10); // 设置第10位
set_bit(bitmap, 100); // 设置第100位
printf("Bit 10 is %s\n", is_bit_set(bitmap, 10) ? "set" : "clear");
printf("Bit 100 is %s\n", is_bit_set(bitmap, 100) ? "set" : "clear");
free(bitmap);
return 0;
}
在此代码中,我们定义了一个位图数组,使用位操作来设置和清除特定的位,并检查位是否被设置。这可以通过使用位掩码和位运算符 | 、 & 和 ~ 来完成。这种方法非常适用于需要频繁设置、清除和检查大量位的场景,比如用户权限管理、缓存机制等。
5. 递归和迭代算法的实际应用
在编程的世界里,算法的设计和实现是构建复杂系统的核心。在众多算法设计范式中,递归和迭代是两种最基础且广泛使用的技巧。它们在解决问题时各有优势,相互补充。本章节将深入探讨递归和迭代算法的设计原理、实际应用,并通过ACM竞赛中遇到的案例分析其在解题中的实战演练。
5.1 递归算法的原理和设计
5.1.1 递归的定义和调用机制
递归是一种自引用的过程,函数调用自身的结构。在递归中,一个复杂问题被分解为一个或多个更小的子问题,直到问题规模缩小到可以直接解决的程度。这种“分而治之”的思想是递归的核心。
一个标准的递归函数包含两个基本部分:
- 基准情形(Base Case):直接给出答案的简单情况,避免无限递归。
- 递归情形(Recursive Case):对问题进行递归求解,并缩小问题规模。
下面以阶乘函数的计算为例,展示一个简单的递归调用过程:
int factorial(int n) {
if (n <= 1) return 1; // 基准情形
return n * factorial(n-1); // 递归情形
}
在这个例子中, factorial 函数直接计算1的阶乘,而对于大于1的 n ,函数会调用自身计算 n-1 的阶乘,并将结果乘以 n 。
5.1.2 递归算法的经典问题分析
递归算法是ACM竞赛中经常考察的内容,它能够优雅地解决许多复杂问题。为了更好地理解递归,在这里我们分析一个经典的递归问题——汉诺塔问题。
汉诺塔问题的目标是将 n 个大小不等的盘子从一个柱子移动到另一个柱子上,且在移动过程中任何时刻大盘子都不可以放在小盘子上面。
void hanoi(int n, char from_rod, char to_rod, char aux_rod) {
if (n == 1) {
printf("Move disk 1 from rod %c to rod %c\n", from_rod, to_rod);
return;
}
hanoi(n - 1, from_rod, aux_rod, to_rod);
printf("Move disk %d from rod %c to rod %c\n", n, from_rod, to_rod);
hanoi(n - 1, aux_rod, to_rod, from_rod);
}
汉诺塔问题的解决策略是:首先将上面的 n-1 个盘子借助目标柱子移动到辅助柱子上,然后将最大的盘子移动到目标柱子上,最后将 n-1 个盘子从辅助柱子移动到目标柱子上。
5.2 迭代算法的原理和设计
5.2.1 迭代的概念和在数据结构中的应用
与递归不同,迭代是通过重复执行一段代码来解决问题的过程。迭代通常需要一个循环结构,如 while 或 for 循环,来重复执行特定的任务,直到满足某个终止条件。
在数据结构中,迭代常常用于遍历和操作结构中的元素。例如,遍历链表、二叉树的层序遍历等。
以简单的二叉树前序遍历为例:
void preorderTraversal(TreeNode* root) {
if (root == NULL) return;
printf("%d ", root->val); // 访问根节点
preorderTraversal(root->left); // 遍历左子树
preorderTraversal(root->right); // 遍历右子树
}
5.2.2 迭代与递归的性能比较及选择策略
在性能方面,迭代通常比递归更加高效,因为它避免了函数调用的开销和递归栈的使用。然而,递归在代码的可读性和简洁性上往往更胜一筹。
在选择使用迭代还是递归时,可以考虑以下因素:
- 复杂度 :递归可能导致较高的时间复杂度和空间复杂度,特别是在有大量重复子问题的情况下。
- 栈空间 :对于深度很大的递归,可能会因为栈溢出而导致程序崩溃。
- 易读性 :在逻辑复杂,或者递归的分解思想较为直观的情况下,使用递归可以使代码更加清晰易懂。
在实际应用中,迭代和递归各有优劣,选择哪种方式取决于具体问题和性能要求。
5.3 递归与迭代在ACM竞赛中的实战演练
5.3.1 算法竞赛中递归与迭代的实际案例
在ACM竞赛中,递归和迭代的使用是解题的关键。考虑一个常见的问题:计算斐波那契数列的第 n 项。
递归实现非常直观:
int fibonacci(int n) {
if (n <= 1) return n;
return fibonacci(n-1) + fibonacci(n-2);
}
然而,递归的指数级时间复杂度使得它在 n 较大时变得不切实际。此时,迭代的线性时间复杂度就显示出了其优势:
int fibonacci(int n) {
if (n <= 1) return n;
int a = 0, b = 1, c = 0;
for (int i = 2; i <= n; i++) {
c = a + b;
a = b;
b = c;
}
return b;
}
5.3.2 常见问题的解题思路与优化技巧
在ACM竞赛中,递归与迭代不仅各自独立应用,还常常结合使用以达到最佳解题效果。例如,在解决图的遍历问题时,可以使用递归来遍历每个连通分量,而在每个连通分量内部使用迭代来遍历节点。
针对递归,优化技巧包括:
- 记忆化(Memoization) :存储已经计算过的子问题结果,避免重复计算。
- 尾递归优化 :某些语言支持尾递归优化,可以将递归转化为迭代,减少栈空间的使用。
针对迭代,优化技巧包括:
- 避免重复计算 :通过一些数据结构(如集合或哈希表)记录已遍历的节点或状态。
- 优化循环条件 :减少每次循环的计算量,例如使用位操作代替模运算。
通过这些策略,我们可以更好地掌握递归和迭代算法,提高解决ACM竞赛问题的效率。
递归和迭代是ACM竞赛中解决问题不可或缺的工具。通过本章节的深入分析,我们学习了它们的工作原理、设计方法和实战演练。随着对这些基本算法范式的掌握,我们将能够更加灵活地应对各种复杂的问题,从而在算法竞赛中脱颖而出。
6. ACM竞赛中数据结构学习的拓展与深化
6.1 数据结构在算法竞赛中的拓展应用
6.1.1 算法竞赛中常用的数据结构选型策略
在算法竞赛中,根据问题的特点选择合适的数据结构是至关重要的。例如,如果需要高效地处理大量数据的查询和更新操作,平衡树(如 AVL 树或红黑树)可能是合适的选择。当面对数据范围较大,但操作相对简单时,可以考虑使用分块或分治策略,利用数组或静态数据结构。
6.1.2 高级数据结构如线段树、树状数组的应用场景
线段树和树状数组是处理区间查询和更新问题的常用高级数据结构。线段树适合处理动态区间查询问题,例如区间最大值、最小值、总和等,且支持点更新和区间更新操作。树状数组(Binary Indexed Tree, BIT)则是一种优化的数据结构,特别适合于一维前缀和查询的场景,并且支持快速的单点更新。
代码示例:使用线段树进行区间求和操作
#define MAXN 1000 // 假设线段树最多处理1000个元素
// 定义线段树的节点结构
struct SegmentTreeNode {
int start, end;
int sum;
} tree[4 * MAXN];
// 构建线段树
void buildTree(int node, int start, int end) {
tree[node].start = start;
tree[node].end = end;
if (start == end) {
tree[node].sum = arr[start]; // arr 是输入的数组
} else {
int mid = (start + end) / 2;
buildTree(2 * node, start, mid);
buildTree(2 * node + 1, mid + 1, end);
tree[node].sum = tree[2 * node].sum + tree[2 * node + 1].sum;
}
}
// 更新线段树
void update(int node, int start, int end, int idx, int val) {
if (start == end) {
arr[idx] += val;
tree[node].sum += val;
} else {
int mid = (start + end) / 2;
if (start <= idx && idx <= mid) {
update(2 * node, start, mid, idx, val);
} else {
update(2 * node + 1, mid + 1, end, idx, val);
}
tree[node].sum = tree[2 * node].sum + tree[2 * node + 1].sum;
}
}
// 查询区间和
int query(int node, int start, int end, int l, int r) {
if (r < start || end < l) {
return 0;
}
if (l <= start && end <= r) {
return tree[node].sum;
}
int mid = (start + end) / 2;
return query(2 * node, start, mid, l, r) + query(2 * node + 1, mid + 1, end, l, r);
}
6.2 数据结构学习的深化与进阶
6.2.1 数据结构与算法的综合应用题目解析
在高级的算法竞赛题目中,数据结构通常与其他算法相结合,以达到更高效的问题解决。例如,使用优先队列(堆)结合 Dijkstra 算法进行图的最短路径求解;利用并查集解决网络连接问题;应用动态规划与线段树的结合实现高效的状态转移。
6.2.2 算法竞赛中的高效算法设计与实现
设计一个高效的算法通常涉及对问题的深入理解,以及对时间、空间复杂度的精细考量。在算法竞赛中,分析问题并选择或构造合适的数据结构是基础,进一步地,还需要结合问题特点,灵活运用各种算法思想,如贪心、动态规划、回溯等,来设计解决方案。
代码示例:使用堆进行优先队列的应用
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
// 定义比较函数,用于优先队列
struct Compare {
bool operator()(const pair<int, int>& a, const pair<int, int>& b) {
return a.second > b.second; // 以第二种元素为比较的主键,使得值最小的优先级最高
}
};
// 使用优先队列实现Dijkstra算法
void dijkstra(int src, vector<vector<pair<int, int>>>& graph) {
int n = graph.size();
vector<int> dist(n, INT_MAX); // 存储源点到每个点的最短距离
priority_queue<pair<int, int>, vector<pair<int, int>>, Compare> pq; // 定义优先队列
dist[src] = 0;
pq.push(make_pair(src, 0)); // 将源点加入优先队列
while (!pq.empty()) {
int u = ***().first;
int d = ***().second; // 获取优先队列顶元素,并更新距离
pq.pop();
if (d > dist[u]) continue; // 如果当前已知距离更短,则忽略该节点
for (auto& edge : graph[u]) {
int v = edge.first;
int weight = edge.second;
// 如果找到更短的路径,则更新距离并加入优先队列
if (dist[u] + weight < dist[v]) {
dist[v] = dist[u] + weight;
pq.push(make_pair(v, -dist[v]));
}
}
}
// 输出从源点到各点的最短距离
for (int i = 0; i < n; ++i) {
cout << "Distance from node " << src << " to node " << i << " is " << dist[i] << endl;
}
}
int main() {
int n, m;
cin >> n >> m; // n为节点数,m为边数
vector<vector<pair<int, int>>> graph(n); // 邻接表表示图
for (int i = 0; i < m; ++i) {
int u, v, w;
cin >> u >> v >> w;
graph[u].push_back(make_pair(v, w)); // 有向图的边
graph[v].push_back(make_pair(u, w)); // 无向图的边
}
dijkstra(0, graph); // 以节点0为源点运行Dijkstra算法
return 0;
}
在算法竞赛中,除了上述示例中使用的数据结构和算法,还应当了解并掌握更多的高级数据结构和算法思想,如并查集、KMP算法、后缀数组等,以及它们在具体问题上的应用。通过不断地实践和深入研究,竞赛参与者可以在数据结构与算法方面取得更深入的理解和更高的成就。
简介:本资料包旨在帮助ACM竞赛参与者深入理解并应用数据结构。通过C语言的讲解,涵盖数组、链表、栈、队列、树、图、哈希表和堆等数据结构的原理及其实现。每个数据结构都包含C语言的代码实例,帮助学习者理解其工作原理并熟练掌握相关算法。掌握这些内容不仅能够提升编程技能,还有助于在ACM及其他编程挑战中取得成功。
























 757
757

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








