
在庞大的工业废水处理市场背景下,采用机械蒸汽再压缩(MVR)技术,对工业废水进行深度处理的同时能够回收得到生产用原材料,实现废水资源化利用。在各类基于MVR技术的蒸发浓缩结晶系统中,单一操作参数对系统性能的影响规律已经得到广泛研究,包括物料浓度、蒸发温度、换热温差、压比等。通过分析影响规律,可对操作参数的取值范围进行优选,使得系统各方面性能达到最优,即系统的参数优化设计。在优化MVR系统操作参数方面,单一操作参数优选研究较多,同时考虑两个及以上决策变量对系统综合性能的影响鲜少研究,属于多变量多目标优化问题。
遗传算法通过模仿自然界的进化机制,能够实现随机全局并行搜索优化,具有简便、快捷、强容错性等优点,已有广泛的应用实例,适用性好且可靠性高。新一代采用精英保留策略的多目标优化算法中最具代表性的为第二代非支配排序遗传算法(NSGA-Ⅱ)和强度Pareto进化算法2(SPEA2),NSGA-Ⅱ应用广泛但容易陷入局部最优,使得解的分布不够均匀[24],而SPEA2适应度分配策略及密度估计技术精确性高,收敛性和多样性更好。经SPEA2优化计算后得到Pareto解集,进一步从中选取最优值不能直接利用数值法,于是引入模糊集合理论,有效地选取Pareto解集中的相对最优解。
本课题组在提出MVR并联双效蒸发结晶系统的基础上,针对系统设计变量间关系复杂,且存在多个性能评价指标的情况,提出基于SPEA2的操作参数多目标优化方法,以系统总功耗和总换热面积为优化目标,通过具体工况下的实例计算,验证了该算法用于系统参数优化的可行性;利用模糊集合理论在最优解集中选出最优参数组合,通过对比分析参数优化前后的系统性能,验证了该算法的有效性。
0 1优化问题描述

MVR并联双效蒸发结晶系统的工艺流程如图1所示,系统中循环的介质包括原料、蒸汽及冷凝水。对于原料液,在预热器中与蒸发器排出的高温冷凝水进行换热至设定的蒸发温度,并以此温度进入降膜蒸发器,利用热源蒸汽进行沸腾换热蒸发;蒸发后剩余的饱和原料液进入强制循环蒸发器进一步蒸发,溶液过饱和而析出晶体;强制循环蒸发器中产生的晶浆通入结晶分离器进行固液分离,晶体进入储存罐,饱和溶液在循环泵作用下回到强制循环蒸发器继续蒸发。对于蒸汽,蒸发器产生的二次蒸汽首先通入气液分离器,去除其中夹杂的液滴后进入蒸汽压缩机,压缩机出口为高温高压的过热蒸汽,利用系统产生的冷凝水对其进行喷淋处理至饱和状态,然后作为蒸发沸腾过程所需的热源蒸汽通入蒸发器。
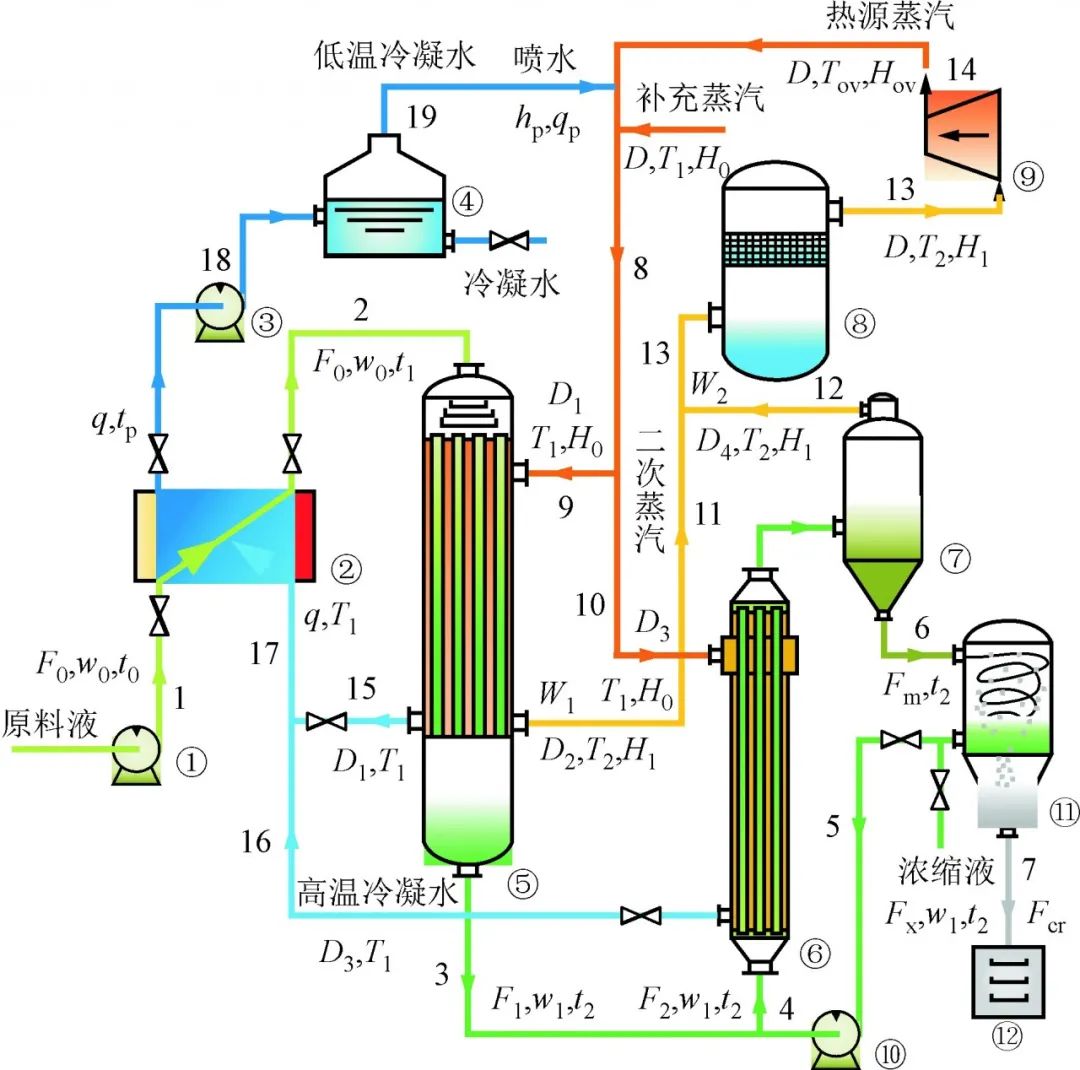
①-原料液泵;②-预热器;③-凝水泵;④-凝水箱;⑤-降膜蒸 发器;⑥-强制循环蒸发加热室;⑦-强制循环蒸发蒸发室; ⑧-气液分离器;⑨-蒸汽压缩机;⑩-循环泵原料液泵; (11)-结晶分离器;(12)-晶体储存罐
对于冷凝水,热源蒸汽放热形成高温冷凝水,经预热器放热后形成低温冷凝水,在冷凝水泵作用下进入凝水罐。其中补充蒸气仅在系统启动阶段或运行过程中热量损失过多时使用。
针对此蒸发结晶系统,在已建立的系统数学模型基础上进行多目标优化,对影响系统性能的关键操作参数进行优选,使系统的能效性和经济性指标达到最优。
0 2优化参数选择

在包含MVR技术的系统中,蒸发器和蒸汽压缩机均为系统循环的核心设备。蒸发器中,蒸发在饱和状态下进行,通过蒸发温度可得对应的蒸发室操作压力,是系统循环中一个重要的影响因素。对于蒸汽压缩机,进口气体为蒸发产生的饱和二次蒸汽,饱和蒸汽经压缩后得到的是过热蒸汽,过热会造成对设备及系统工作效率的误判,因此在MVR技术中的压缩温升定义为进出口蒸汽实际压力对应的饱和温度之差。压缩温升是系统能量循环重要的驱动力,提供蒸发器中的换热温差并且克服溶液沸点升的影响,因此选取蒸发温度和压缩温升作为优化变量。
评价MVR蒸发结晶系统性能的主要指标有系统的功耗量、总换热面积、效能系数(COP)等,其中系统功耗量决定了系统的运行费用,在蒸发量一定的条件下决定了COP的大小,而换热面积与系统初投资及系统体积紧密相关。因此,选取系统总功耗和总换热面积为优化目标。
通过系统模拟及数据验证,蒸发温度和压缩温升对系统能耗和总换热面积有较大影响。在相同蒸发量、进料量且进料温度恒定的条件下,蒸发温度保持不变,压缩温升对系统能耗和总换热面积的影响规律见图2a。相同限定条件下,压缩温升保持不变,蒸发温度对系统能耗和总换热面积的影响规律见图2b。
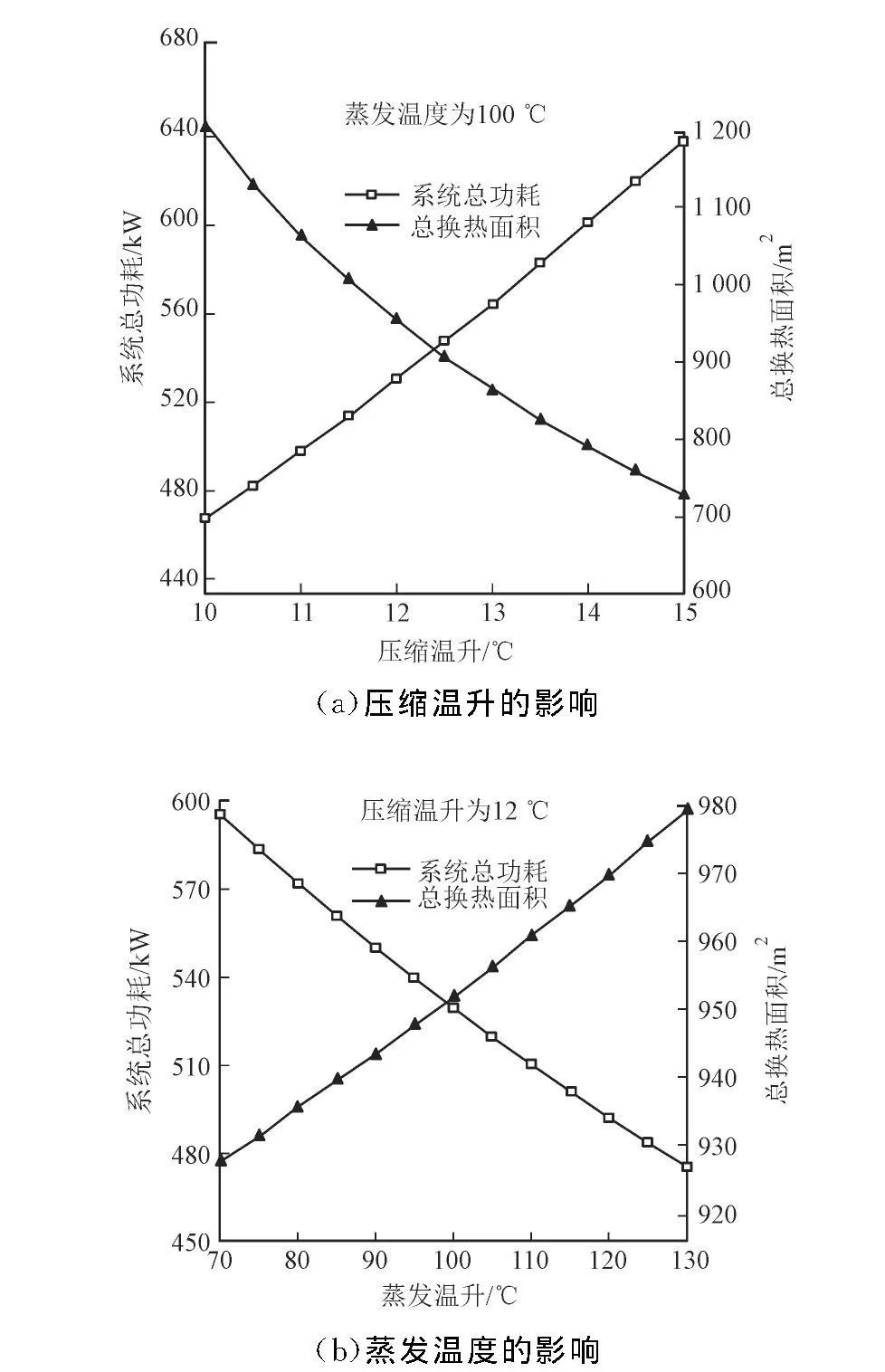
如图2a所示,在蒸发温度保持不变的情况下,随着压缩温升增加,系统总功耗增大,主要原因在于压缩温升增大表示压缩机的压比增大,蒸汽压缩机的工作量增大,所以总功耗增大;总换热面积随压缩温升的增加而减小,是因为在相同蒸发换热量的情况下,换热温差增大,所需换热面积减小。综上可以看出,在蒸发温度一定时,存在一个最佳的压缩机饱和温升,使得系统总功耗和总换热面积都相对较小。如图2b所示,在压缩温升保持不变的情况下,随着蒸发温度升高,系统总功耗降低,原因在于,高蒸发温度会使进入压缩机的二次蒸汽温度和压力较高,提升同样的温度和压力值,功耗少于低蒸发温度的情况,总换热面积随蒸发温度升高有小幅度提升。在压缩温升一定的条件下,同样存在一个最佳的蒸发温度,使得系统总功耗和总换热面积都相对较小。
由系统的稳态数学模拟结果可知,在蒸发量、进料量及进料温度恒定的前提下,只以减小系统功耗为优化目标会造成换热面积过大,进而造成系统初始投资高、占地面积大等问题;只以减小换热面积为优化目标又会使系统功耗过大,系统的运行成本提高且不符合节能的要求。因此,压缩温升和蒸发温度两个操作参数存在一个相对最佳组合值,使得系统总功耗和总换热面积都较小。
0 3优化模型

3.1 目标函数
(1)以系统总换热面积最小为优化目标。
总面积包括降膜蒸发器换热面积S1、强制循环蒸发器换热面积S2,以及对原料液进行预热处理时的板式换热器换热面积S0。用x1和x2分别表示蒸发温度及压缩温升,函数关系式如下:

式中:r0为热源蒸汽的汽化潜热,即对压缩机出口蒸汽进行喷水处理后的饱和蒸汽潜热值。预热器冷凝水出口温度tp除与x1的直接关系外,还是蒸发温度x1的函数,关系式为

计算面积时,涉及的蒸发器换热温差由压缩温升x2承担。
(2)以系统的总功耗最小为优化目标。
由计算实例数据得到,系统中主要耗能设备为蒸气压缩机和强制循环蒸发器,泵和分离器的能耗仅占系统总能耗的2.9%,所以优化计算将其忽略[29]。总功耗的函数表达式为

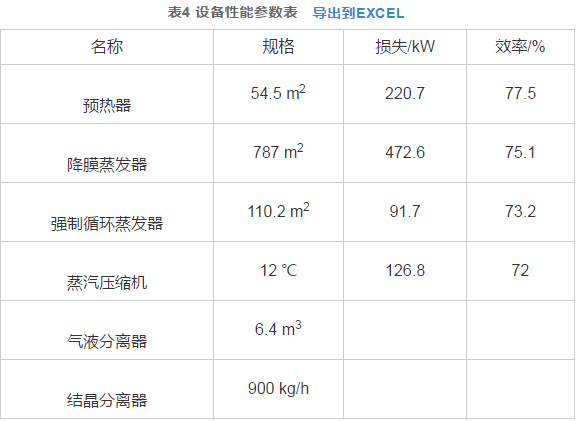
式中:D2+D4代表压缩机进气量,通过对两个蒸发器分别建立能量守恒可得[29]。压缩机进、出口压力Pin、Pout对应于该压力状态下进、出口蒸汽的饱和温度T,压缩温升x2对压缩机功耗的影响通过Pin、Pout体现,蒸发温度x1通过影响压缩机进口温度进而影响压缩机功耗。对于强制循环蒸发器的能耗,在设计过程中通过单位加热面积的功率消耗经验值0.4~0.8 kW[30]计算,本设计选取0.6 kW。
3.2 约束条件及决策变量取值范围
参数优化过程中只有将除决策变量外的其他影响因素都考虑在内,优化才更具实际意义。在本系统中,原料液进料质量流量、温度及浓度等会使系统的功耗和换热面积发生变化,针对系统的物料平衡及能量平衡方面,约束条件描述如下。
(1)物料平衡约束

(2)能量平衡约束

(3)决策变量取值范围
模型中决策变量的取值范围对优化结果有较大影响,通过经验类比[11,12,13],决策变量取值范围如表1所示。其中Xmax、Xmin分别为上、下限值,Xini为初始设计值。

3.3 计算模型验证
为验证系统计算模型的可行性及准确性,以文献[11]设计参数为输入值,将本系统模型计算的结果与文献[11]的数据结果进行对比,如表2所示。从表中可得,在相同给定参数条件下,本文计算结果与文献计算结果的误差最大为13.3%,处于较小范围内,因此该计算模型能够在一定的误差范围内对系统进行模拟计算。



4.1 搜索过程
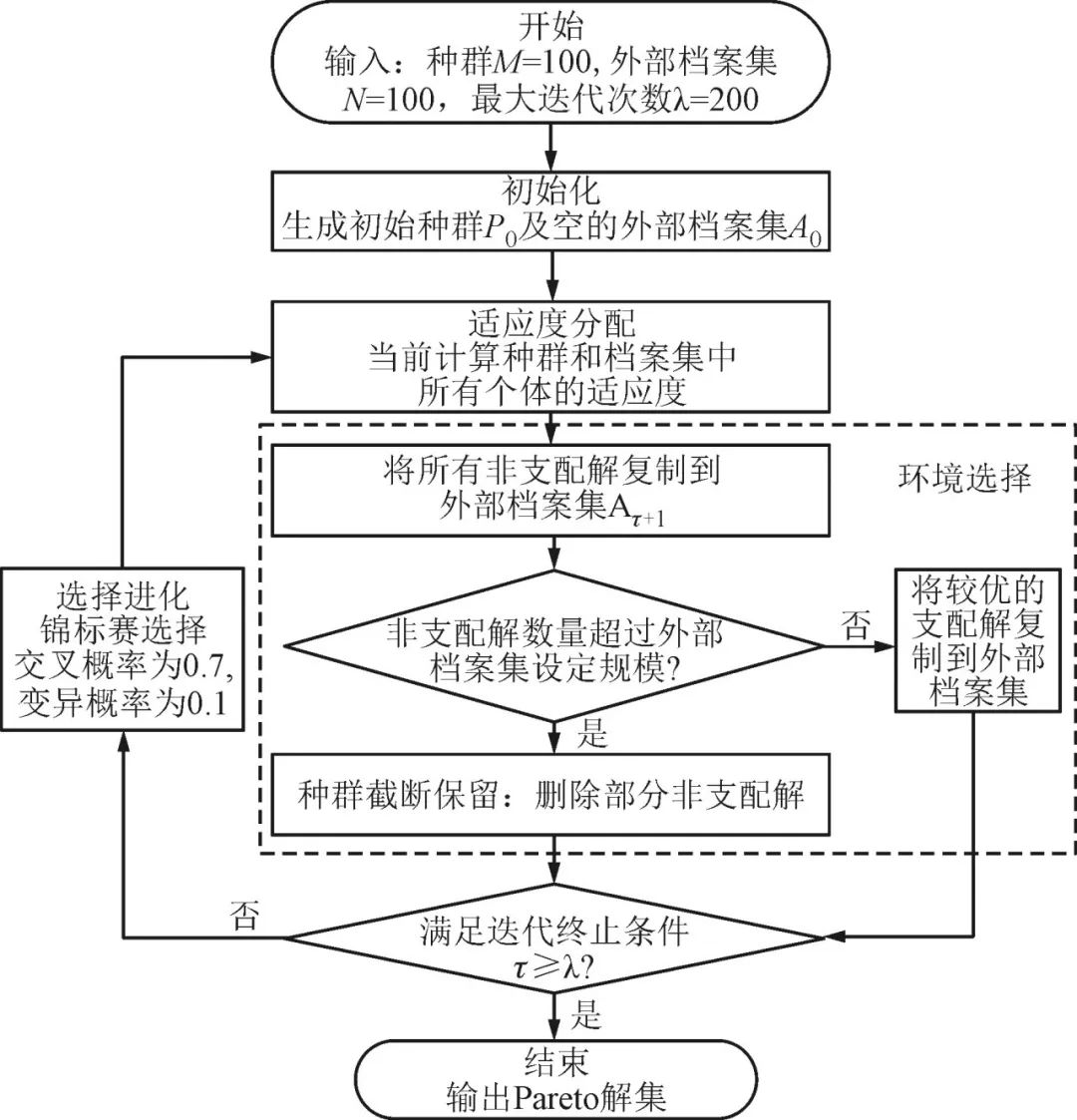
SPEA2算法能够在较快的运算速度下,达到精确性较高的适应度分配策略、密度估计及截断保留方法,在收敛性和解的多样性方面表现优越,是比较成熟且具有代表性的多目标进化算法。SPEA2优化算法的流程如图3所示,实现过程如下。
(1)输入:种群M、外部档案集N以及最大迭代次数λ;
(2)初始化:当前迭代次数τ=0,生成初始种群P0,并创建空的外部档案集A0;
(3)适应度分配:计算当前计算种群Pτ和外部档案集Aτ中所有个体的适应度值;
(4)环境选择:将Pτ和Aτ中的非支配解都复制到Aτ+1中,通过判断Aτ+1中个体数量与设定外部档案集N的关系,进行种群截断保留或补全;
(5)迭代终止条件:当τ≥λ时,将当前档案集Aτ+1中的非支配解输出为Pareto最优解集,算法结束;
(6)交叉及变异:未满足迭代终止条件时,Aτ+1中的个体将经锦标赛选择后,进行交叉及变异过程产生新个体,此过程后的迭代次数加1,种群调整为Pτ+1,回到步骤。
对优化目标函数、决策变量及约束条件进行实数编码,其中涉及的蒸汽汽化潜热、压缩机进出口蒸汽压力、饱和蒸汽及饱和冷凝水焓值等均通过《水和水蒸气热力性质图表》[31]查得。以文献[29]提出的MVR并联双效蒸发结晶系统在常压操作工况下的计算结果为原始数据,通过SPEA2进化算法对该系统进行优化设计,系统的原始设计任务参数见表3,设备性能参数见表4。

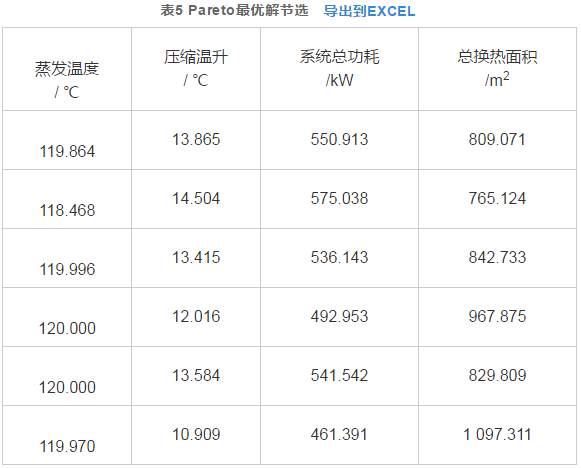
通过MATLAB运行算法得到Pareto最优前沿如图4所示,表5所列为部分最优解集数值。
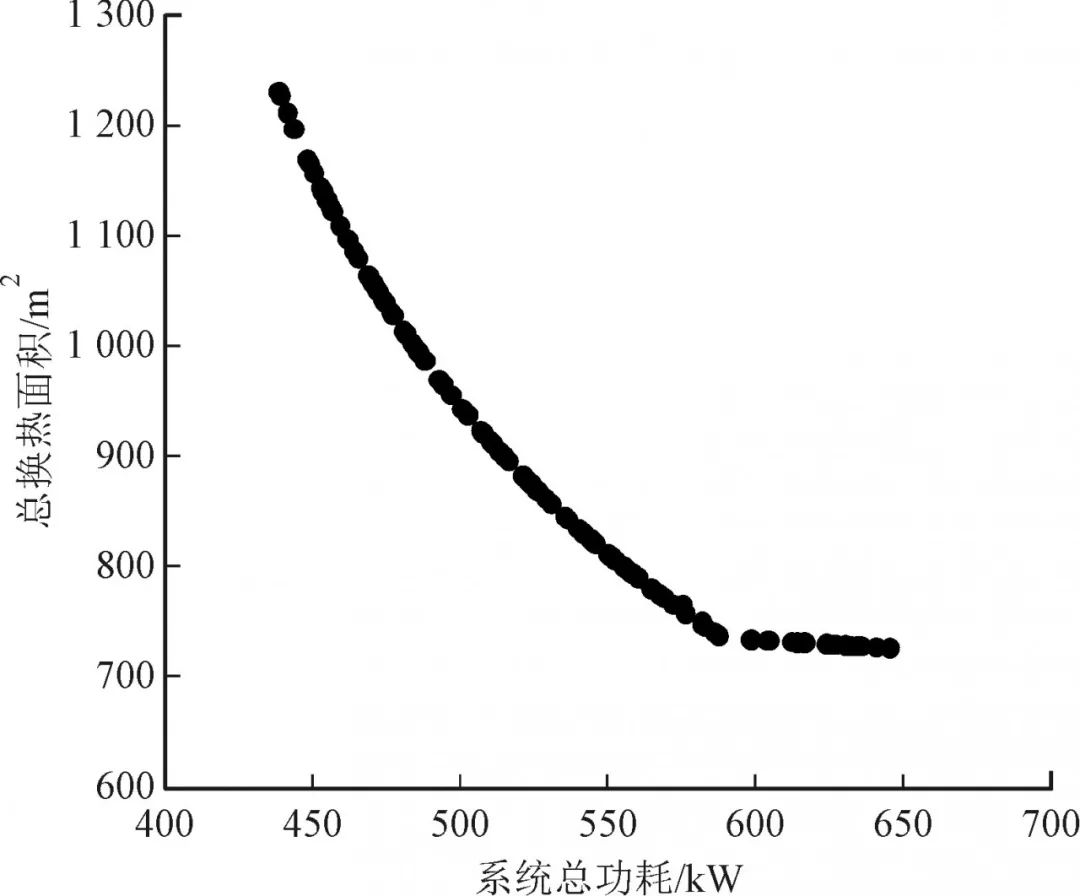
4.2 决策过程
Pareto最优解集中包含大量非劣解,针对其无法进行数值大小对比和选择的问题,采用模糊集合理论对Pareto最优解集进行预选,在此基础上,再结合工程实际精度选取最优值。
模糊集合理论以相对隶属度为基石,通过建立相关的隶属函数来量化表示事物的亦此亦彼性,能够为选取Pareto最优解集中的相对最优解提供有效判据,定义隶属函数为

式中:fmin,i和fmax,i分别为第i个优化目标的最小值和最大值;fi为第i个优化目标的取值。
对于Pareto最优解集中的每一个非支配解k,定义其对剩余其他解的支配函数为

式中:Mp为Pareto最优解集所包含解的个数,本计算中Mp=100;Mo为优化目标的个数,这里Mo=2。
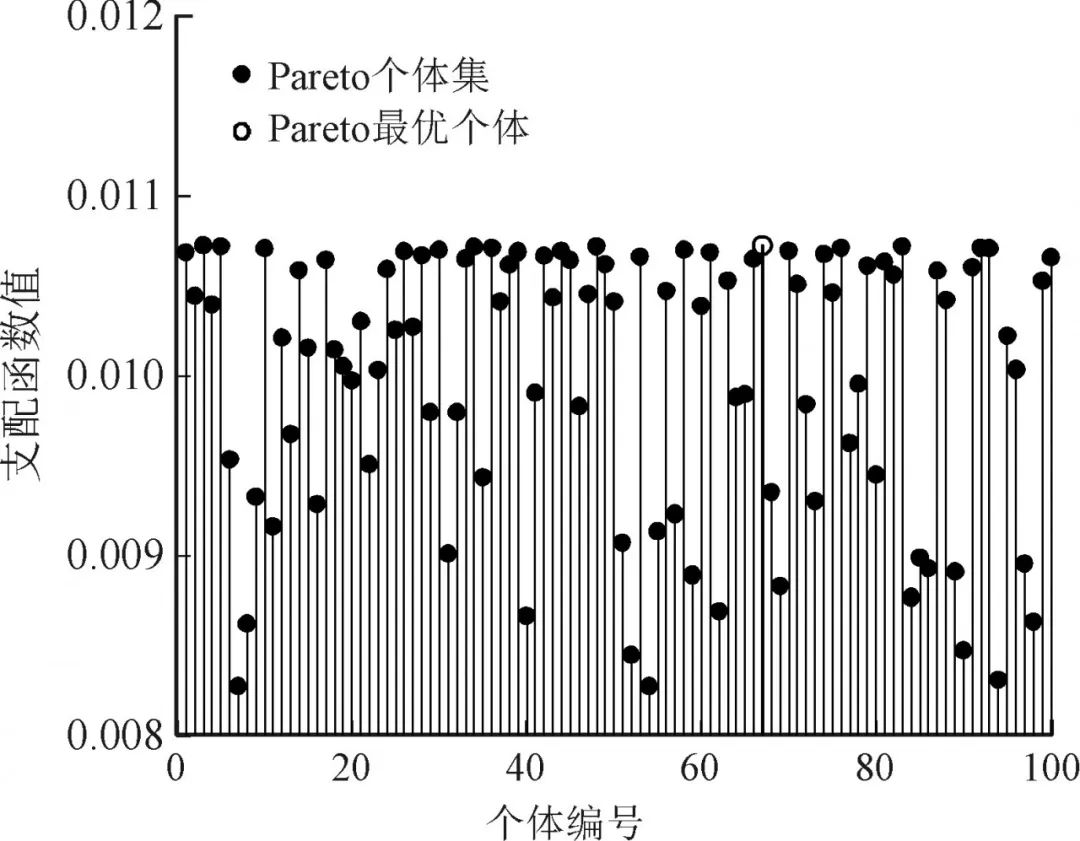
根据式(15)可以计算Pareto最优解集中每个个体对其他个体的支配值,Φk越大表示该解对其他解的支配度越大,对应综合性能越好,因此选择具有最大Φk的解初步作为最优解。图5所示为将Pareto最优前沿对应的解进行模糊决策后得到的所有个体的支配值,因计算中种群规模设置得比较大,所以在个体分布上多样性和均匀性较好。其中,编号为67的个体支配函数值最大,最大支配函数值为0.010 7,对应的优化结果见表6。

4.3 结果讨论
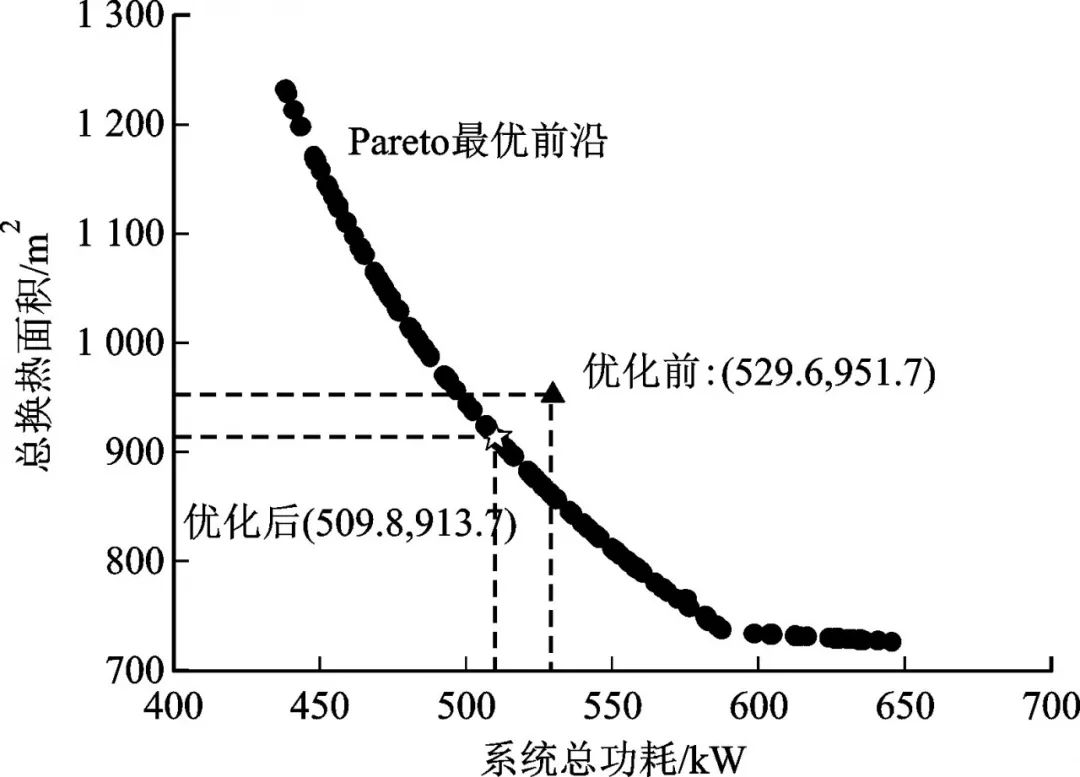
考虑到实际工程对温度的控制精度,在模糊集合选优的基础上,最终优化后的压缩温升定为12.5 ℃,蒸发温度定为120 ℃。将常压操作工况[29]和优化后的操作参数工况表示在图6中,根据Pareto占优概念,优化后的工况点占优于优化前,系统总功耗和总换热面积两个优化目标都有所降低。对优化前后表示系统性能的参数进行对比计算,结果见表7。
由表7可知, 优化后的蒸发温度和压缩温升有不同程度的升高,在相同蒸发量条件下,优化目标值均减小,其中系统总功耗降低了22.1 kW,总换热面积减少了31.2 m2。以优化后的操作参数组合进行模拟计算,系统COP提高了7.94%,效率提升了5.91%,表明优化后的操作条件下,系统能量利用率增大,损失减小了38.4 kW,说明优化后的系统热力学完善程度更高。在相同设计任务参数条件下,将SPEA2进化算法应用于蒸发温度和压缩机饱和温升的组合值优选,相比初步设计中根据经验选择两者的组合值,能够降低系统的总功耗和总换热面积,提高系统的整体性能。

分析系统总功耗降低的原因有:蒸发温度提高,压缩机进出口蒸汽温度也有所提高,进出口蒸汽压力发生变化,计算得到的压缩机压比减小,所以功耗相应减小;虽从压缩温升提高的层面看,压缩机功耗上升,但增幅很小,整体功耗下降。又因优化后强制循环蒸发器的换热面积减小,功耗相应减小,所以系统总功耗减小。
分析总换热面积减小的原因有:压缩温升包含两部分的作用,第一部分是作为有效温差加热溶液,第二部分是克服溶液沸点升高带来的影响。只提高压缩温升时,溶液沸点升高的影响不变,则提供给第一部分的温升增大,即换热温差增大,所以蒸发器换热面积减小。从蒸发温度升高的角度分析,预热器换热量增大,且幅度大于其换热温差增大幅度,预热器换热面积增大。整体来看,蒸发器换热面积的降幅的影响大过预热器换热面积增幅的影响,所以总换热面积减小。
对于其他系统性能评价指标,COP增大是因为相同蒸发量下,溶液蒸发吸收的热量相同,优化后系统总功耗降低。系统效率的提升及损失下降,原因在于蒸发温度升高,使循环中的蒸汽、冷凝水值增大,系统可用能提高。根据效率计算公式,收益增大,而支付即系统总功耗减小,因此系统效率提高、损失减小,单位蒸发量能耗随总功耗降低而减小。
0 5结 论

(1)系统总功耗随着压缩温升增大相应增大,总换热面积则相应减少;蒸发温度升高会使系统总功耗降低,同时总换热面积增大。特定蒸发量下,压缩温升和蒸发温度两个参数存在一个最优组合,使系统总功耗和总换热面积都相对较小。
(2)应用SPEA2多目标优化遗传算法搜索最优解,可以弥补只针对单一决策变量进行选优时,评价系统性能综合程度的不足;采用模糊集合理论进行最优解决策,比人工经验选取更具准确性和参考意义。
(3)优化后,在相同蒸发量条件下,系统总功耗降低22.1 kW,总换热面积减少31.2 m2,即对应的系统运行费用和初投资均有所降低;COP提高7.94%,效率提升5.91%,表明系统能量利用率更高,热力学完善程度也得到改善。转自:西安交通大学学报 作者:张子尧 姜华 宫武旗
























 1444
1444

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








