不等式两边加绝对值_重点解析丨不等式求解方法归纳（优选）

今天包sir 给大家分享一份超全的“不等式求解”方法，对于这部分知识比较薄弱的同学，可以来系统的复习啦！

不等式基本知识

1

基本性质

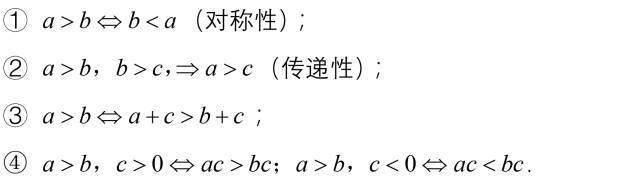
2

运算性质

3

常用不等式

▼

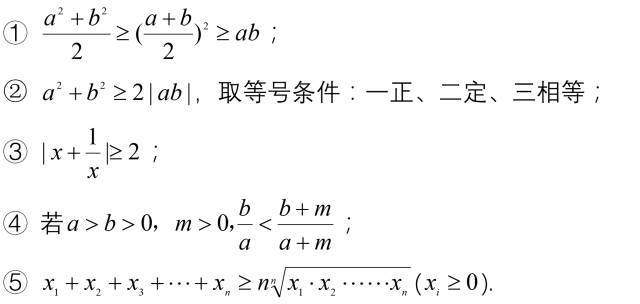
不等式的证明方法

常用的方法有：比较法、分析法、综合法、归纳法、反证法、类比法、放缩法、换元法、判别式法、导数法、几何法、构造函数、数轴穿针法等。

1

比较法

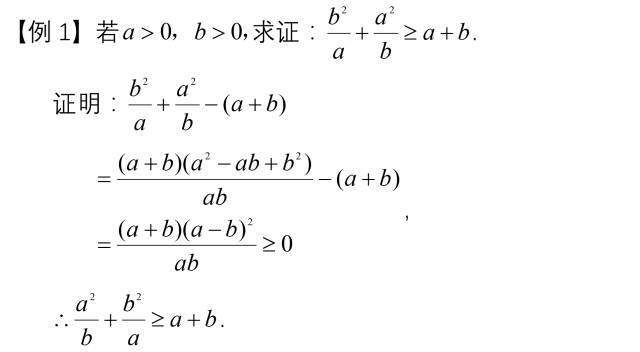
2

分析法

3

综合法

4

数学归纳法

5

反证法

6

类比法

7

放缩法

常用放缩公式：

8

换元法

常用换元方法：

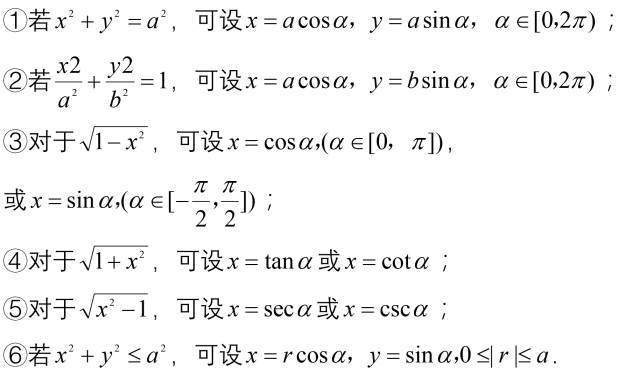
9

判别式法

10

导数法（单调性）

11

构造函数法

12

数轴穿针法

▼

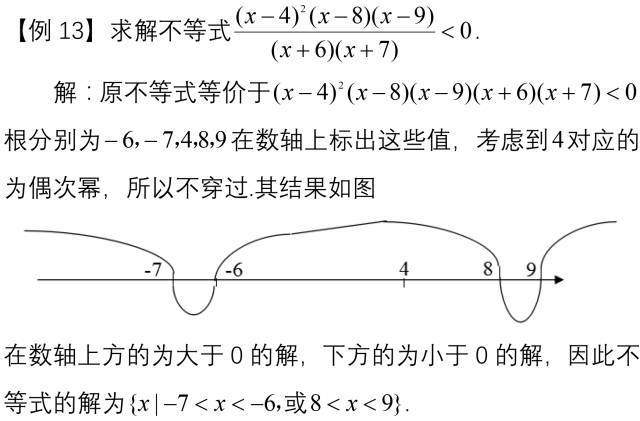
含绝对值不等式的解法

1

分类讨论

2

两边平方法（承接例1）

3

图像法

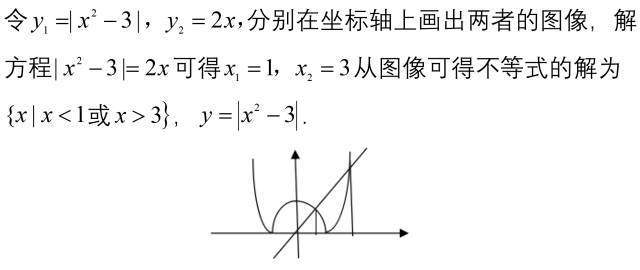
4

等价转化法（承接例1）

5

运用线性规划求解

6

运用绝对值的几何意义

▼

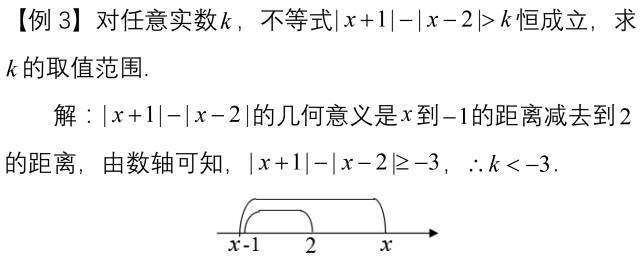
含参一元二次不等式例解

含有参数的不等式应用的比较多的是分类讨论思想，①其思路是一般先将式子因式分解或分解因式或分母有理化，然后再结合参数对称轴、判别式、根的正负进行讨论；②当无法进行因式分解的时候多涉及对称轴或者利用导数求解，下面结合例题解析。

1

二次项不含参数

2

二次项含参数

▼

不等式恒成立问题

1

恒成立问题的基本类型

恒成立问题的解题的基本思路是：根据已知条件将恒成立问题向基本类型转化，正确选用函数法、最小值法、数形结合等解题方法求解。

2

利用判别式解

3

利用分离常数解

4

利用变换参数来解

（该法适用于题中已给出参数的界限）

5

利用最值

6

数形结合

▼

练习题

声明：文章转载自高中数学解题研究会333528558；如存在文章/图片/音视频使用不当的情况，或来源标注有异议等，请联系我们第一时间处理。

只有掌握这些答题技巧，考试时才能攻无不克，战无不胜~拔得头筹~

更多有效学习方法，快来关注包sir 哟~